Hier finden Sie alle relativen Positionen zweier Linien im Raum (in R3). Darüber hinaus wird erklärt, wie man die relative Position zwischen zwei Linien mithilfe der beiden möglichen Methoden ermittelt: anhand von Bereichen oder anhand eines Punktes und eines Vektors jeder Linie. Sie können sogar Beispiele und Übungen sehen, die Schritt für Schritt gelöst werden.
Was sind die relativen Positionen zweier Linien im Raum?
In der analytischen Geometrie gibt es beim Arbeiten in einem dreidimensionalen Raum (in R3) 4 mögliche relative Positionen zwischen zwei Linien: Zwei Linien können Verschmelzungslinien , parallele Linien , Sekantenlinien oder Sekantenlinien sein.
Parallele Linien

Zwei Geraden sind parallel, wenn sie die gleiche Richtung haben, aber keinen gemeinsamen Punkt haben. Außerdem haben parallele Linien immer den gleichen Abstand voneinander.
zusammenfallende Linien

Zwei Geraden fallen zusammen, wenn sie die gleiche Richtung haben und darüber hinaus alle ihre Punkte gemeinsam sind.
Schnittlinien

Zwei sich schneidende Linien haben unterschiedliche Richtungen, berühren sich aber an einem Punkt.
Schnittlinien

Zwei sich schneidende Linien haben unterschiedliche Richtungen und schneiden sich an keinem Punkt. Daher liegen zwei gekreuzte Linien nicht in derselben Ebene. Beispielsweise in der grafischen Darstellung oberhalb der Linie
![]()
ist immer einen Schritt voraus
![]()
, sodass sie sich niemals berühren werden.
Es gibt zwei Möglichkeiten, die relative Position zwischen zwei Linien zu ermitteln, da diese davon abhängen, wie die Gleichungen der beiden Linien ausgedrückt werden:
- Wenn die Linien in Vektor-, parametrischer oder kontinuierlicher Gleichungsform vorliegen, ist es am besten , die relative Position aus einem Punkt und einem Vektor jeder Linie zu berechnen (die Erklärung dieser Methode finden Sie weiter unten).
- Wenn die Linien andererseits in Form impliziter (oder allgemeiner) Gleichungen definiert sind, ist es einfacher , die relative Position zwischen den beiden Linien zu ermitteln, indem der Rang zweier Matrizen berechnet wird (siehe Erklärung unten).
Bestimmen der relativen Position zweier Linien aus einem Punkt und einem Vektor
Sie können die relative Position zwischen zwei Linien ermitteln, indem Sie für jede Linie einen Punkt und einen Vektor angeben. Diese Methode eignet sich, wenn die Linien in Form einer Vektorgleichung, parametrischer Gleichungen oder einer kontinuierlichen Gleichung definiert sind.
Der Richtungsvektor und jeder Punkt auf jeder der beiden Geraden seien also:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bdc3a31a3a5a8aa3da312bb2badb356_l3.png)
Um also die relative Position zweier Linien zu ermitteln, müssen wir das folgende Verfahren befolgen:
‣ Als Erstes müssen wir prüfen, ob die Vektoren der beiden Geraden proportional sind oder nicht, und je nach Fall gehen wir wie folgt vor:
- Wenn die beiden Vektoren proportional sind, können die Geraden parallel sein oder zusammenfallen. Wir müssen daher prüfen, ob der Punkt einer Geraden die Gleichung der anderen Geraden erfüllt:
- Wenn der Punkt einer Geraden die Gleichung der anderen Geraden erfüllt, bedeutet das, dass die beiden Geraden zusammenfallen.
- Andernfalls bedeutet dies, dass die beiden Geraden parallel sind.
- Wenn die beiden Vektoren nicht proportional sind, können sich die Linien schneiden oder schneiden. In diesem Fall müssen wir die folgende 3×3-Determinante lösen:
![Rendered by QuickLaTeX.com \begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-84a440053c71b2d4287cf246ff1d2f4b_l3.png)
- Wenn die vorherige Determinante gleich Null ist, schneiden sich die beiden Geraden in einem Punkt (sie schneiden sich).
- Wenn die vorherige Determinante von Null verschieden ist, schneiden sich die beiden Geraden.
Die folgende Grafik fasst den gesamten Ablauf zusammen:
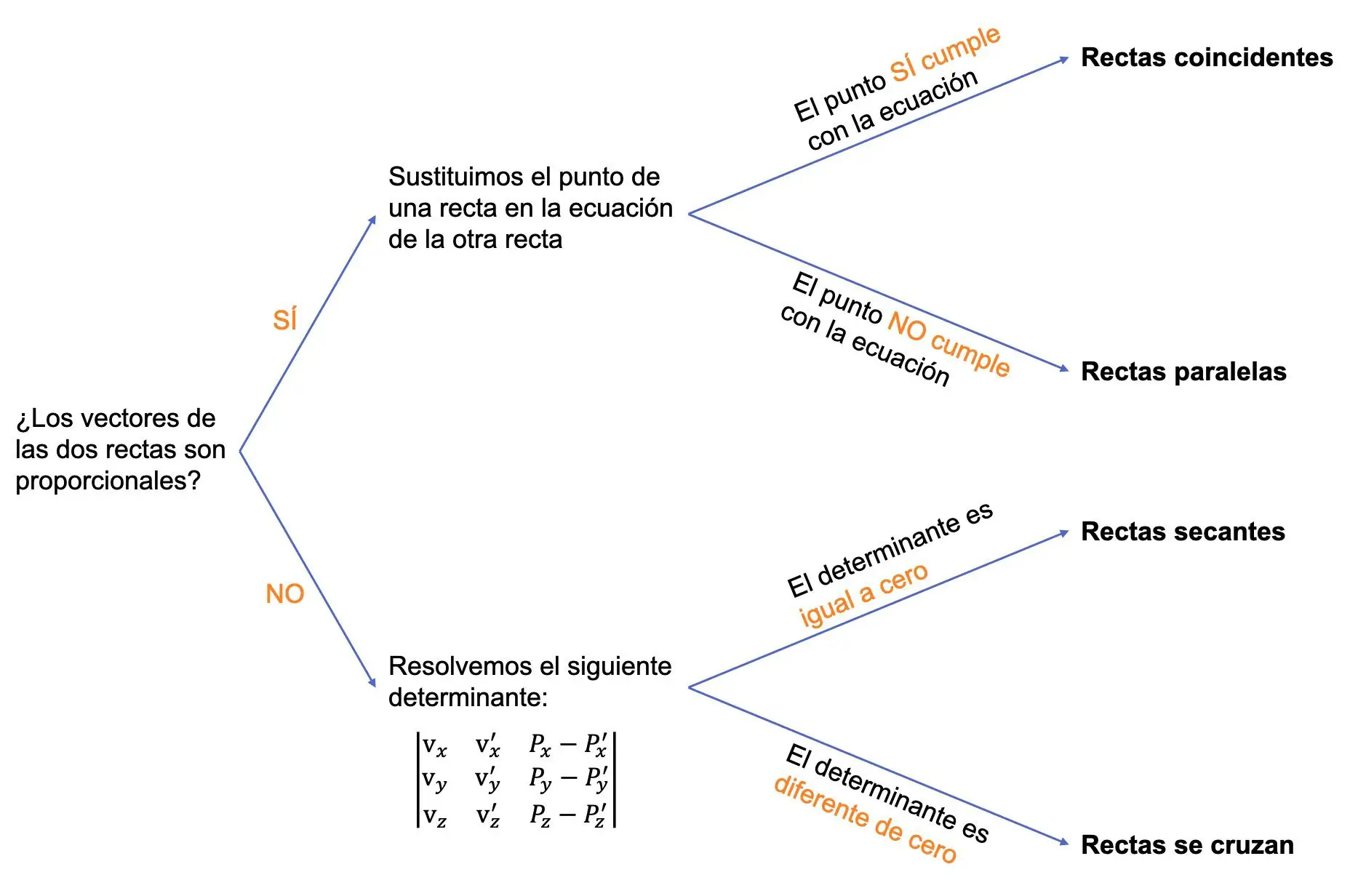
Beispiel für die Bestimmung der relativen Position zwischen zwei Linien
Die vorherige Vorgehensweise mag etwas kompliziert erscheinen, aber damit Sie sehen, dass es das Gegenteil ist, lösen wir beispielhaft ein Problem:
- Bestimmen Sie die relative Position zwischen den folgenden beiden Zeilen:
![]()
![]()
Die beiden Linien werden als Vektorgleichung ausgedrückt, wobei der Richtungsvektor jeder Linie ist:
![]()
Und ein Punkt, durch den jede Gerade verläuft, ist:
![]()
Sobald wir einen Punkt und den Richtungsvektor jeder Linie kennen, wenden wir die oben beschriebene Methode an. Zunächst müssen wir prüfen, ob die Koordinaten der Vektoren proportional sind:
![]()
Da die beiden Vektoren nicht proportional zueinander sind, können sich die Linien nur berühren oder kreuzen. Daher müssen wir nun nach der folgenden Determinante suchen, die aus dem Richtungsvektor und einem Punkt auf jeder Linie besteht:
![Rendered by QuickLaTeX.com \begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-225a68c152f54a250471b7c4c2254b89_l3.png)
Wir setzen die Werte in die Formel ein:
![Rendered by QuickLaTeX.com \begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fac3bc2228451f94261e296aeecb5de6_l3.png)
Und wir berechnen die Determinante, hierfür können Sie jede Methode verwenden (Sarrus-Regel, Methode der Komplemente oder Cofaktoren usw.):
![Rendered by QuickLaTeX.com \begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-538af230a8105fceefc5a30f41237ea3_l3.png)
Wäre das Ergebnis der Bestimmung Null gewesen, würde dies bedeuten, dass sich die Linien kreuzen (sie berühren sich). Da die Determinante jedoch von 0 verschieden ist, schneiden sich die Geraden .
Finden Sie die relative Position zweier Zeilen für Zeilen
Eine andere Möglichkeit, die relative Position zweier Zeilen zu ermitteln, besteht darin, die Ränge zweier konkreter Matrizen zu berechnen, wie wir als Nächstes sehen werden. Diese Methode ist sehr nützlich, wenn die beiden Linien in impliziter (oder allgemeiner) Gleichungsform vorliegen.
Wenn wir also zwei Linien haben, die mit ihren impliziten (oder allgemeinen) Gleichungen in einem dreidimensionalen Raum (in R3) ausgedrückt werden:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-500405383e97627c17d01023fd9dd198_l3.png)
![Rendered by QuickLaTeX.com \displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c96b6990dae5ce476ee55689cf4f4fb_l3.png)
Sei A die Matrix, die sich aus den Koeffizienten der beiden Geraden zusammensetzt:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9199790c5f157691d9307604f25fc873_l3.png)
Und angesichts der erweiterten Matrix A‘, die aus allen Parametern der beiden Linien besteht:
![Rendered by QuickLaTeX.com \displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f087aea2d9209341c2acf240eab2bc77_l3.png)
Dann kann die relative Position der beiden Zeilen anhand des Bereichs der beiden vorherigen Matrizen gemäß der folgenden Tabelle bestimmt werden:

Um die relative Position zwischen zwei Zeilen zu ermitteln, müssen wir daher die Ränge der beiden Matrizen berechnen. Abhängig vom Rang jeder Matrix wird es den einen oder anderen Fall geben.
Dieser Satz kann mit dem Satz von Rouché-Frobenius (einer Methode zur Lösung linearer Gleichungssysteme) bewiesen werden. Auf dieser Seite werden wir den Beweis jedoch nicht durchführen, da er recht umständlich ist und nicht viel hinzufügt.
Beispiel dafür, wie man die relative Position zweier Linien anhand von Bereichen ermittelt
Nachdem wir die Theorie über die relativen Positionen zwischen zwei Zeilen für Zeilen kennengelernt haben, sehen wir uns anhand eines Beispiels an, wie sie in die Praxis umgesetzt wird:
- Finden Sie die relative Position der folgenden zwei Zeilen:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d930886e4afd4cd3b14f1bd788c6da5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7704e8cf4de26fa0c249eaabdefa4150_l3.png)
Da die beiden Geraden die Form allgemeiner (oder impliziter) Gleichungen haben, verwenden wir die Rangfolgemethode, um die relative Position zwischen den beiden Geraden zu ermitteln. Wir konstruieren daher die Matrix A und die erweiterte Matrix A‘ mit den Koeffizienten der Geraden:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3726bfaa82678d1fffdbae281882572a_l3.png)
Sobald wir beide Matrizen haben, müssen wir den Rang jeder Matrize berechnen. Wir berechnen zunächst den Rang der Matrix A anhand der Determinanten:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e643845acc44a30e16f7628e85955d0_l3.png)
![]()
Matrix A enthält die Determinante einer 3×3-Submatrix ungleich Null, sodass Matrix A den Rang 3 hat .
Und nun berechnen wir den Umfang der erweiterten Matrix A‘. Die Matrix A‘ wird immer mindestens den Rang der Matrix A haben, die in diesem Fall den Wert 3 hat, es genügt also zu prüfen, ob sie Rang 4 oder Rang 3 hat. Dazu lösen wir die Determinante der 4×-Matrix 4 durch Additionen (oder Cofaktoren):
![]()
![Rendered by QuickLaTeX.com \displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd21ed058cb7405e6aee811315086225_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f99f68649b9ca6274e4531a1d172315_l3.png)
![]()
![]()
![]()
![]()
Die Determinante der gesamten erweiterten Matrix ist Null, daher hat die Matrix A‘ ebenfalls den Rang 3 .
Die Matrix A und die Matrix A‘ haben also den Rang 3, sodass sich die beiden Geraden folglich schneiden . Das heißt, es gibt nur einen Schnittpunkt zwischen ihnen.
![]()
Denken Sie daran, dass Sie oben eine Tabelle haben, die alle möglichen Fälle relativer Positionen zwischen zwei Linien entsprechend den Bereichen der Matrizen A und A‘ zusammenfasst.
Probleme der relativen Position zwischen zwei Linien im Raum gelöst
Übung 1
Finden Sie die relative Position zwischen den folgenden beiden Zeilen:
![]()
![]()
Da beide Geraden als Vektorgleichung ausgedrückt werden, ermitteln wir die relative Position zwischen den beiden Geraden anhand der Ein-Punkt- und Ein-Vektor-Methode für jede Gerade.
Der Richtungsvektor jeder Linie ist:
![]()
Und zu jeder Geraden gehört ein Punkt:
![]()
Um das Verfahren anwenden zu können, muss daher zunächst geprüft werden, ob die Komponenten der Richtungsvektoren proportional sind:
![]()
Da die beiden Vektoren nicht proportional zueinander sind, können sich Geraden nur schneiden oder schneiden. Daher müssen wir nun die folgende Determinante ermitteln, die aus dem Richtungsvektor und einem Punkt auf jeder Geraden besteht:
![Rendered by QuickLaTeX.com \begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-225a68c152f54a250471b7c4c2254b89_l3.png)
Wir setzen die Werte in die Formel ein:
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5b88268ae0a4248a6289d0f789250a9_l3.png)
Und wir berechnen die Determinante:
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-99043262ed64a3fce660dc55e943a93a_l3.png)
Das Ergebnis des Bestimmers ist äquivalent zu 0, die Geraden schneiden sich also.
Übung 2
Berechnen Sie die relative Position der folgenden zwei Linien:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1848a24fa2901265ca9b0d141c7e2d4b_l3.png)
Die erste Linie hat die Form parametrischer Gleichungen und die zweite Linie hat die Form einer kontinuierlichen Gleichung, mit der wir die relative Position zwischen den beiden Linien anhand der Ein-Punkt-Vektor-Methode jeder Linie bestimmen.
Die Koordinaten des Richtungsvektors rechts
![]()
sind die Koeffizienten vor dem Parameter
![]()
und die Koordinaten des Richtungsvektors der Linie
![]()
sind die Zahlen der Nenner:
![]()
Und zu jeder Geraden gehört ein Punkt:
![]()
Um das Verfahren anwenden zu können, muss daher zunächst geprüft werden, ob die Komponenten der Richtungsvektoren proportional sind:
![]()
Die beiden Vektoren sind proportional zueinander, sodass die Geraden nur parallel oder zusammenfallend sein können. Um diesen Zweifel auszuräumen, ist es notwendig, den Punkt auf der Linie zu ersetzen
![]()
in der Geradengleichung
![]()
(oder umgekehrt), um zu sehen, ob es die Gleichung erfüllt:
![]()
![]()
![]()
![]()
Durch Einsetzen des Punktes in der Geraden erhalten wir eine Gleichheit, sodass der Punkt einer Geraden die Gleichung der anderen Geraden erfüllt und außerdem ihre Richtungsvektoren proportional sind. Daher fallen die beiden Linien zusammen.
Übung 3
Finden Sie die relative Position der folgenden zwei Zeilen:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-33fbac4dc2933022ff39a0ed9d457200_l3.png)
![Rendered by QuickLaTeX.com \displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8afae699c3b46dc2153236605e254fdc_l3.png)
Die beiden Linien haben die Form einer allgemeinen (oder impliziten) Gleichung, daher verwenden wir die Rangmethode, um die relative Position zwischen den beiden Linien zu ermitteln. Wir erstellen daher die Matrix A und die erweiterte Matrix A‘ mit den Koeffizienten der Linien:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6133960b0b951ec6c455384a1b2274c5_l3.png)
Sobald wir beide Matrizen haben, müssen wir den Rang jeder Matrize berechnen. Wir berechnen zunächst den Rang der Matrix A anhand der Determinanten:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-85353e6e57de74332ffdb3d5cd44caaa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d33b143e636093057c08fbcd9d91ab54_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b4b570b6d9d92b7974b11afbe0939bd_l3.png)
![]()
Alle 3×3-Determinanten der Matrix A sind Null, aber es gibt eine 2×2-Determinante ungleich Null innerhalb der Matrix, sodass Matrix A den Rang 2 hat .
Und nun berechnen wir den Umfang der erweiterten Matrix A‘. Die Matrix A‘ wird immer mindestens den Bereich der Matrix A haben, der in diesem Fall 2 beträgt. Daher muss überprüft werden, ob sie eine 3×3-Determinante hat, die sich nicht aufhebt, und auch, wie groß die Determinante von ist gesamte Matrix:
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d253c404b2ac9caf3119795e80acfbfb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-8744aa6a413d43832344c6eba827c7e6_l3.png)
![]()
Die erweiterte Matrix A‘ enthält tatsächlich 3×3 Nicht-Null-Unterdeterminanten und darüber hinaus ist die Determinante der gesamten erweiterten Matrix gleich 0, sodass die Matrix A‘ den Rang 3 hat .
Die Matrix A hat also den Rang 2 und die Matrix A‘ den Rang 3, sodass die beiden Geraden parallel sind . Das heißt, sie haben nichts gemeinsam.
![]()
Denken Sie daran, dass Sie in der Erläuterung der Methode (oben) eine Tabelle haben, die alle möglichen Fälle relativer Positionen zwischen zwei Linien entsprechend den Rängen der Matrizen A und A‘ zusammenfasst.
Übung 4
Finden Sie die relative Position der folgenden zwei Zeilen:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b39d8ac101e2b4db7f5a17a3f27066b5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ddbbfa691034e2f7acd17d6391e9719e_l3.png)
In diesem Fall liegen die beiden Linien in kartesischer (oder impliziter) Gleichungsform vor, daher verwenden wir die Ordnungsmethode, um die relative Position zwischen den beiden Linien zu ermitteln. Wir konstruieren daher die Matrix A und die erweiterte Matrix A‘ mit den Koeffizienten der Geraden:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cfc6a66630bf6a5cc24f5a006db629af_l3.png)
Sobald wir die beiden Matrizen kennen, müssen wir deren Rang berechnen. Wir berechnen zunächst den Rang der Matrix A anhand der Determinanten:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7a682d947fc58cb847cb2dd60f8772d8_l3.png)
![]()
Matrix A enthält eine 3×3-Submatrix, deren Determinante ungleich Null ist, sodass Matrix A den Rang 3 hat .
Und nun berechnen wir den Umfang der erweiterten Matrix A‘. Die Matrix A‘ wird immer mindestens den Rang der Matrix A haben, die in diesem Fall den Wert 3 hat. Es genügt also zu prüfen, ob sie Rang 4 oder Rang 3 hat. Dazu lösen wir die Determinante von die Menge der 4×4-Matrix durch Additionen (oder Cofaktoren):
![]()
![Rendered by QuickLaTeX.com \displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc223e99519a7cc9359cb6e08591e039_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed6f0611953cbd025d6e3bed38994fe1_l3.png)
![]()
![]()
![]()
![]()
Die Determinante der gesamten erweiterten Matrix ist ungleich Null, daher hat die Matrix A‘ den Rang 4 .
Damit die Matrix A den Rang 3 hat und die Matrix A‘ dagegen den Rang 4 hat, schneiden sich die beiden Geraden in einem Punkt.
![]()
Denken Sie daran, dass Sie in der Erläuterung des Verfahrens (oben) eine Tabelle haben, in der alle möglichen Fälle relativer Positionen zwischen zwei Linien entsprechend den Rängen der Matrizen A und A‘ aufgeführt sind.