Auf dieser Seite erklären wir, wie man die Ruffini-Regel zur Division von Polynomen anwendet. Zusätzlich zur Erklärung können Sie Beispiele und Schritt für Schritt gelöste Übungen zur Division von Polynomen mit der Ruffini-Regel sehen. Darüber hinaus finden Sie alle Anwendungen dieser Methode und tatsächlich werden Sie sicherlich mehr als eine davon überraschen.
Was ist Ruffinis Regel?
In der Mathematik ist die Ruffini-Regel eine algebraische Methode, die es Ihnen ermöglicht, jedes Polynom schnell durch Polynome der Form xr zu dividieren. Ruffinis Regel ist nach dem Mathematiker Paolo Ruffini benannt, der diese Methode erfunden hat.
Die Ruffini-Regel wird jedoch nicht nur zur Division von Polynomen verwendet, sondern hat auch viele andere Verwendungsmöglichkeiten. Ruffinis Regel wird beispielsweise auch verwendet, um die Wurzeln eines Polynoms zu finden, den numerischen Wert eines Polynoms zu ermitteln, ein Polynom zu faktorisieren oder sogar Gleichungen dritten Grades oder höher zu lösen. Im Folgenden werden wir sehen, wie die Ruffini-Regel angewendet wird, um alle diese Operationen durchführen zu können.
Schließlich ist die Ruffini-Regel auch als Ruffinis-Methode, Ruffinis-Theorem oder synthetische Division von Polynomen bekannt.
So wenden Sie die Ruffini-Regel an
Wie wir gesehen haben, besteht der Hauptzweck der Ruffini-Regel darin, ein Polynom durch ein Binomial zu dividieren, d. h. eine Division der folgenden Art durchzuführen:
![]()
Beachten Sie, dass das Divisionspolynom zur Verwendung der Ruffini-Regel immer aus einem x (mit einem Koeffizienten gleich 1) und einer Zahl (positiv oder negativ) gebildet werden muss, andernfalls kann der Ruffini-Algorithmus nicht verwendet werden.
Um die Ruffini-Regel anzuwenden, muss ein ganzes Verfahren befolgt werden. Im Folgenden werden wir daher Schritt für Schritt ein Beispiel lösen, um zu sehen, wie die Ruffini-Regel (oder die Ruffini-Methode) angewendet wird.
Beispiel für Ruffinis Regel
- Lösen Sie die folgende Division von Polynomen mithilfe der Ruffini-Regel:
![]()
Zuerst müssen Sie zwei senkrechte Linien zeichnen, die sich schneiden, und dann den Dividenden und den Divisor wie folgt platzieren:
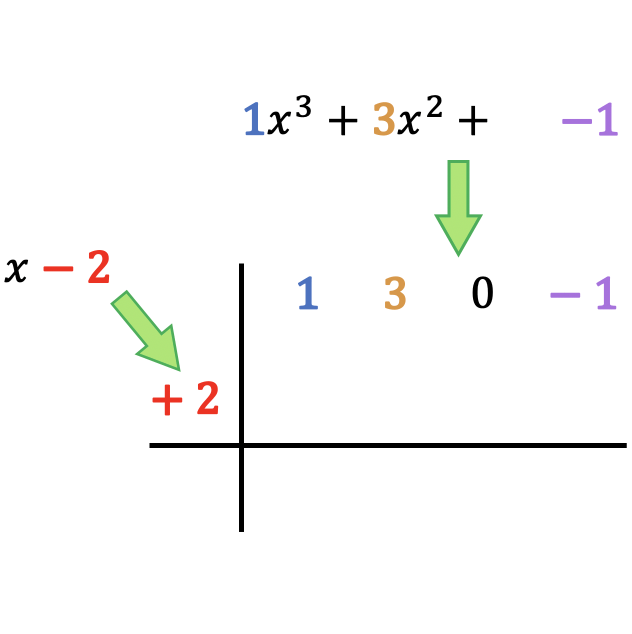
Wie Sie sehen, müssen wir die Koeffizienten des Dividendenpolynoms oben platzieren, geordnet vom höchsten zum niedrigsten Grad, und den unabhängigen Term des Divisorpolynoms links vom Kästchen mit Vorzeichenwechsel platzieren.
Achtung: Wenn das Dividendenpolynom keinen Term eines bestimmten Grades hat (unvollständiges Polynom), wird an seiner Stelle eine 0 eingefügt. In diesem Fall zum Beispiel das Polynom
![]()
Es gibt kein Monom vom Grad 1, also setzen wir an seiner Stelle eine 0.
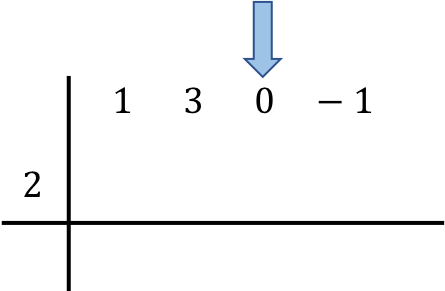
Sobald wir die an der Operation beteiligten Polynome positioniert haben, senken wir die erste Zahl direkt in die Zeile darunter ab:
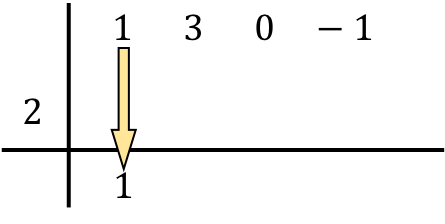
Jetzt kommt der Schritt, der Ruffinis Regel charakterisiert: Wir multiplizieren die Zahl unten mit der Zahl links und tragen das Ergebnis in die folgende Spalte ein :
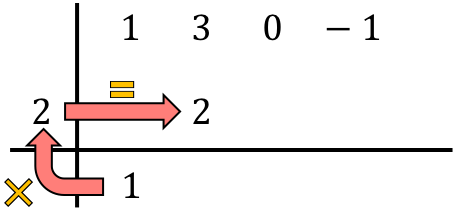
Und wir addieren die Zahlen in der Spalte und tragen das Ergebnis der Summe direkt darunter ein:
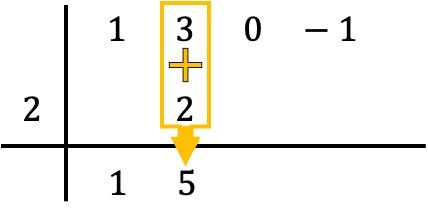
Ruffinis Methode besteht also darin, diesen Vorgang zu wiederholen. Also machen wir das Gleiche noch einmal: Wir multiplizieren die untere Zahl mit der Zahl links, tragen das Ergebnis in die nächste Spalte ein und addieren schließlich die vertikal ausgerichteten Zahlen:
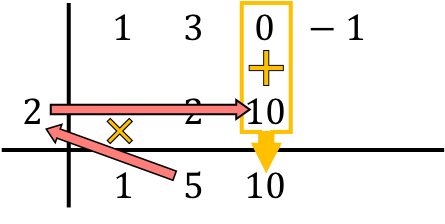
Und wir wiederholen den gleichen Vorgang nacheinander bis zum Ende. Wir bilden zunächst das Produkt der Zahl unten mit der Zahl links, dann tragen wir das Ergebnis in die nächste Spalte ein und addieren schließlich die Zahlen in derselben Spalte:
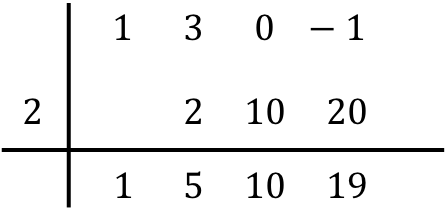
Wenn wir also alle Spalten gefüllt haben, bedeutet das, dass wir mit der Division der Polynome fertig sind.
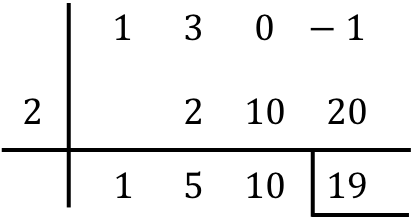
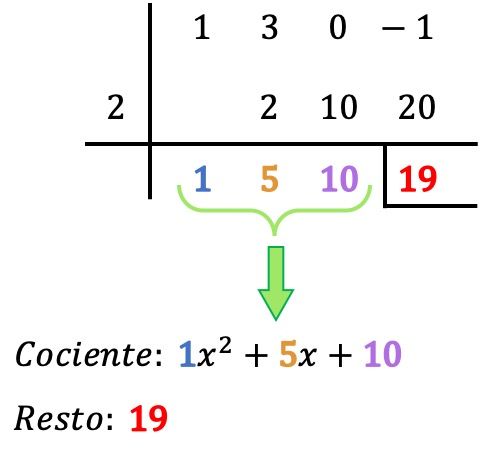
Sie müssen also nur das Ergebnis der Division der Polynome finden:
- Der Rest der Division zwischen den beiden Polynomen ist die letzte Zahl in der Zeile darunter, also ist der Rest in unserem Fall gleich 19. Der Rest wird normalerweise durch Platzieren eines Balkens links und eines weiteren unterhalb der Zahl angezeigt.
- Der Quotient der Polynomdivision wird durch die anderen erhaltenen Werte bestimmt, die die Koeffizienten des Polynomquotienten sind. Die erste Ziffer von rechts entspricht dem Koeffizienten des Semesters der Note 0, die nächste Ziffer dem Koeffizienten des Semesters der Note 1, die nächste der Note 2, die nächste der Note 3 usw. bis zum Ende. . ALSO:
Gelöste Übungen von Ruffinis Herrschaft
Nachfolgend finden Sie mehrere gelöste Schritt-für-Schritt-Übungen zur Ruffini-Regel, damit Sie üben und verstehen können, wie Sie mit dieser Methode Divisionen von Polynomen lösen. Wir empfehlen Ihnen, jede Übung auszuprobieren und anschließend anhand der Korrektur zu überprüfen, ob Sie sie richtig ausgeführt haben.
Übung 1
Führen Sie die folgende Division von Polynomen mit der Ruffini-Regel durch:
![]()
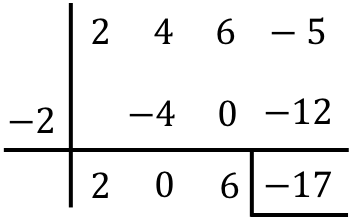
Das Ergebnis der Division zwischen den beiden Polynomen ist daher:
Quotient:
![]()
Ausruhen:
![]()
Übung 2
Berechnen Sie die folgende Division von Polynomen mithilfe der Ruffini-Regel:
![]()
In diesem speziellen Fall hat das Dividendenpolynom keinen Term zweiten Grades, daher müssen wir an seiner Stelle eine Null setzen:
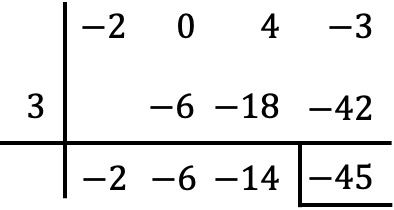
Das Ergebnis der Division zwischen den beiden Polynomen ist daher:
Quotient:
![]()
Ausruhen:
![]()
Übung 3
Finden Sie das Ergebnis der folgenden Division von Polynomen nach der Ruffini-Regel:
![]()
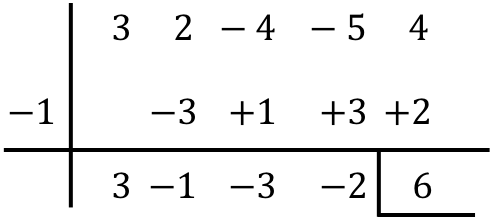
Zusammenfassend ist das Ergebnis der Division der beiden Polynome:
Quotient:
![]()
Ausruhen:
![]()
Übung 4
Finden Sie den Wert der Unbekannten m , sodass der Rest der folgenden Division der Polynome äquivalent zu 5 ist:
![]()
Da der Divisor die Form (xr) oder (x+r) hat, können wir Ruffinis Regel anwenden, um die Division zu lösen. Wir wenden daher Ruffinis Methode an, indem wir das unbekannte m ziehen:
Nun gleichen wir den erhaltenen Rest auf 5 aus, da der Rest 5 sein muss:
![]()
Und wir lösen die Gleichung, um den Wert des Parameters m zu finden:
![]()
![]()
Wenn also die Variable m gleich 3 ist, ist der Rest der Division zwischen den Polynomen gleich 5.
Übung 5
Bestimmen Sie den Wert des Parameters m so, dass der Rest der folgenden Polynomdivision 3 ergibt:
![]()
Da der Divisor die Form (xr) oder (x+r) hat, können wir Ruffinis Regel anwenden, um die Division zu lösen. Daher verwenden wir Ruffinis Methode, indem wir das unbekannte m ziehen:
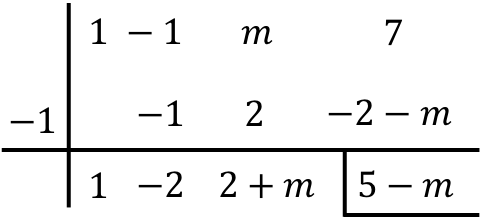
Beachten Sie bei der letzten Multiplikation die Verteilungseigenschaft:
![]()
Andererseits lautet die Berechnung des Rests der Division:
![]()
![]()
![]()
Wir gleichen nun den resultierenden Restausdruck mit 3 aus, da der Rest der Division gleich 3 sein muss:
![]()
Und wir lösen die resultierende Gleichung, um den Wert des Parameters m zu bestimmen:
![]()
![]()
![]()
![]()
Daher muss m gleich 2 sein, damit der Rest der Polynomdivision gleich 3 ist.
Weitere Anwendungen von Ruffinis Regel
Wie erläutert, wird die Ruffini-Regel hauptsächlich zur Division zwischen Polynomen verwendet. Die Ruffini-Regel wird jedoch auch zur Durchführung anderer Berechnungen verwendet, wir werden sie unten einzeln sehen.
Wurzeln eines Polynoms
Die Wurzeln eines Polynoms lassen sich leicht mit der Ruffini-Regel bestimmen. Wenn Sie nicht wissen, was die Wurzel eines Polynoms ist, sehen wir uns seine Definition an:
Die Wurzeln (oder Nullstellen) eines Polynoms sind die Werte, die das Polynom aufheben. Oder anders ausgedrückt: Die Wurzeln eines Polynoms sind alle Werte, die bei der Auswertung im Polynom einen Zahlenwert gleich 0 haben.
![]()
Andererseits wissen wir dank des Restsatzes , dass der numerische Wert eines Polynoms für einen gegebenen Wert gilt
![]()
Null ist, notwendigerweise der Rest der Division des Polynoms zwischen
![]()
Es muss auch 0 sein.
![]()
Wenn Sie also die Ruffini-Regel verwenden, um ein Polynom zu dividieren
![]()
zwischen einem anderen Polynom der Form
![]()
wir erhalten einen Rest gleich 0, das bedeutet das
![]()
ist eine Wurzel des Polynoms
![]()
Anhand eines Beispiels werden wir es sicherlich besser verstehen:
- Überprüfen Sie, ob
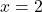
ist eine Wurzel des Polynoms
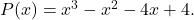
Um zu überprüfen, ob der angegebene Wert eine Wurzel des Polynoms ist, wenden Sie einfach die Ruffini-Methode mit dem Polynom und dem Wert an:
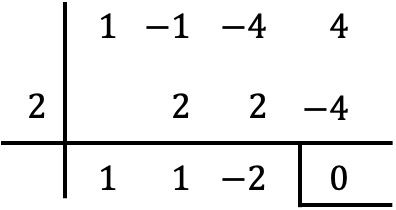
Da der durch Ruffinis Regel erhaltene Rest gleich Null ist, bedeutet dies effektiv
![]()
ist eine Wurzel des Polynoms
![]()
Faktorisierung von Polynomen
Die Ruffini-Regel ist die Methode, die üblicherweise auf faktorielle Polynome angewendet wird, da sie es Ihnen ermöglicht, schnell alle Wurzeln eines Polynoms vom Grad 3, 4, 5 usw. zu kennen.
Sehen wir uns also anhand eines Beispiels an, wie man ein Polynom mit Ruffinis Algorithmus faktorisiert:
- Faktorisieren Sie das folgende Polynom dritten Grades:
![]()
Als Erstes müssen alle Wurzeln des Polynoms ermittelt werden. Und die möglichen Wurzeln eines Polynoms sind die Teiler des unabhängigen Termes, der in diesem Fall 6 ist. Also:
Mögliche Wurzeln des Polynoms: +1, -1, +2, -2, +3, -3, +6, -6
Wir müssen nun versuchen, das Polynom zwischen jedem dieser Werte mit der Ruffini-Regel zu dividieren. Wenn der Rest der Division 0 ist, bedeutet dies, dass der Wert eine Wurzel des Polynoms ist; Wenn der Rest der Division jedoch nicht 0 ist, ist der Wert keine Wurzel des Polynoms. Das Testen der Ruffini-Regel mit allen Zahlen hebt den Rest also nur in den folgenden drei Fällen auf:
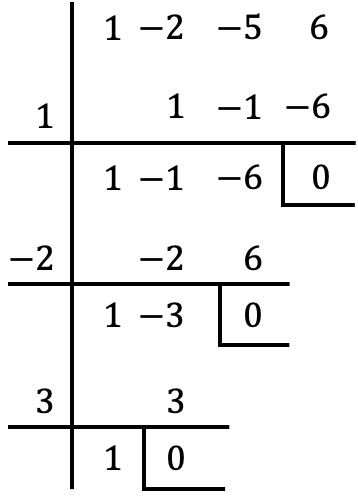
Daher sind die Wurzeln des Polynoms im Problem die Werte, mit denen der Rest verschwindet, also:
![]()
Um schließlich das Polynom zu faktorisieren, müssen wir jede Wurzel ausdrücken
![]()
in Form eines Faktors vom Typ
![]()
, das heißt, dass Sie für jede Wurzel eine Klammer mit a setzen müssen
![]()
und die gefundene Wurzel hat das Vorzeichen geändert:
![]()
Wie Sie sehen, ist es uns gelungen, das Polynom mithilfe der Ruffini-Regel erfolgreich zu faktorisieren. Möglicherweise hatten Sie jedoch Zweifel an der Faktorisierung von Polynomen, da es sich um ein sehr komplexes Thema handelt. In diesem Fall können Sie auf unserer Website (in der Suchmaschine oben rechts) nach dem Artikel suchen, den wir zur Faktorisierung von Polynomen haben. Dort erklären wir ihn ausführlicher und Sie können damit Schritt für Schritt gelöste Übungen üben. Darüber hinaus zeigen wir Ihnen auch andere Methoden zur Faktorisierung von Polynomen.
Berechnen Sie den numerischen Wert eines Polynoms
Obwohl es überraschend erscheinen mag, kann der numerische Wert eines Polynoms durch Ruffinis Regel unter Verwendung des Restsatzes bestimmt werden.
Aber dazu müssen Sie natürlich den Restsatz kennen. Sollte dies nicht der Fall sein, können Sie auf unserer Website (in der Suchmaschine oben rechts) nach der Erklärung des Restsatzes suchen .
Dank des Restsatzes können wir also den numerischen Wert jedes Polynoms kennen. Sehen wir uns anhand eines Beispiels an, wie das geht:
- Berechnen Sie den numerischen Wert von

Für
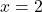
Anwendung von Ruffinis Regel, Sein
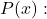
![]()
Den numerischen Wert des Polynoms für den Wert ermitteln
![]()
Das Einzige, was wir tun müssen, ist die Ruffini-Regel mit dem Polynom und dem besagten Wert zu verwenden:
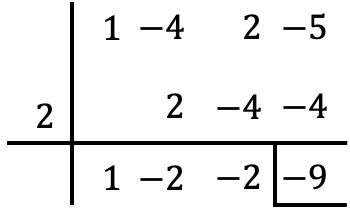
Aus dem Restsatz wissen wir also, dass der numerische Wert des Polynoms mit dem Rest der Polynomdivision übereinstimmt . Daher ist der numerische Wert des Polynoms in
![]()
ist -9.
![]()
Andererseits können wir überprüfen, ob die Ruffini-Regel korrekt angewendet wird, indem wir den Zahlenwert numerisch berechnen:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Lösen Sie Gleichungen dritten Grades oder höher
Eine weitere Anwendung der Ruffini-Regel besteht darin, Gleichungen mit einem Grad größer als 2 zu lösen, da es in diesen Fällen keine Formel wie in der Gleichung zweiten Grades gibt. Sehen wir uns anhand eines Beispiels an, wie das geht:
- Lösen Sie die folgende quadratische Gleichung mit der Ruffini-Regel:
![]()
Wir müssen die Gleichung so behandeln, als wäre sie ein Polynom. Dann müssen wir so viele Wurzeln des „Polynoms“ mithilfe der Ruffini-Regel berechnen, bis wir eine Gleichung zweiten Grades erhalten . In diesem Fall handelt es sich um eine Gleichung vom Grad 3, es reicht also aus, eine Wurzel des „Polynoms“ zu bestimmen:
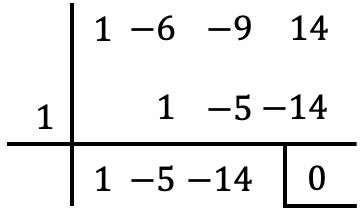
Eine Lösung der Gleichung wird daher sein
![]()
Nun, um die anderen Lösungen zu finden, müssen wir das im Quotienten der Ruffini-Regel erhaltene Polynom gleich 0 setzen:
![]()
Und nun lösen wir die resultierende quadratische Gleichung mit der entsprechenden Formel:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
Zusammenfassend sind die drei Lösungen der Gleichung dritten Grades:
![]()