Auf dieser Seite erfahren Sie, was die Cramer-Regel ist und außerdem finden Sie Beispiele und Übungen zur Lösung von Gleichungssystemen nach der Cramer-Regel.
Was ist Cramers Regel?
Die Cramer-Regel ist eine Methode zur Lösung von Gleichungssystemen nach Determinanten. Mal sehen, wie es verwendet wird:
Betrachten Sie ein Gleichungssystem:
![Rendered by QuickLaTeX.com \begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e0141f3451719f665ef28e4061489551_l3.png)
Die Matrix A und die erweiterte Matrix A‘ des Systems sind:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d628a13ec7de4b3ba7a301c0a5d8ac6_l3.png)
Die Cramer-Regel besagt, dass die Lösung eines Gleichungssystems ist:
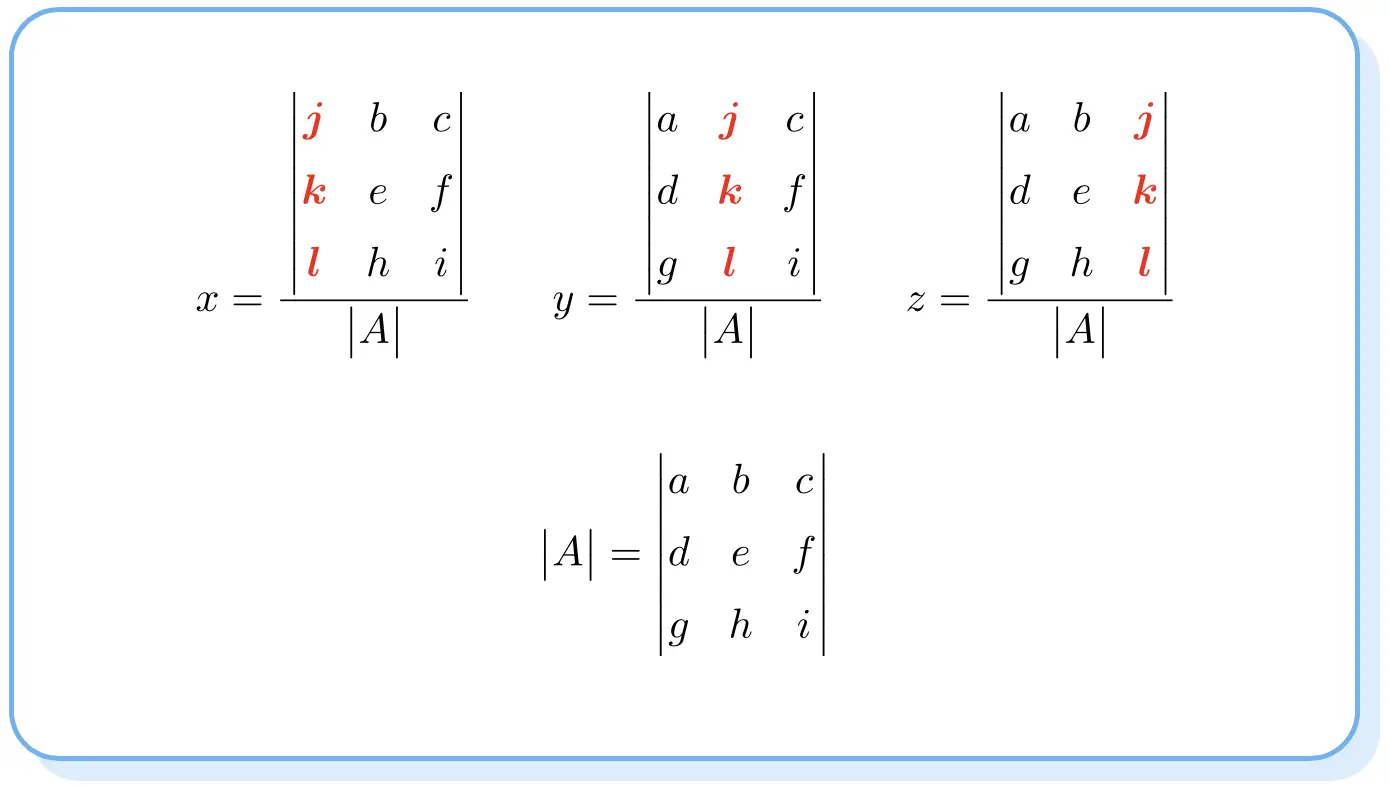
Beachten Sie, dass die Determinanten der Zähler wie die Determinanten der Matrix A sind, jedoch die Spalte jedes Unbekannten in die Spalte unabhängiger Terme geändert wird.
Daher wird die Cramer-Regel zur Lösung linearer Gleichungssysteme verwendet. Aber wie Sie bereits wissen, gibt es viele Möglichkeiten, ein Gleichungssystem zu lösen, zum Beispiel ist die Methode von Gauß Jordan bekannt.
Nachfolgend finden Sie Beispiele für die Lösung linearer Gleichungssysteme mit der Cramer-Regel, manchmal auch als Kramer-Regel geschrieben.
Beispiel 1: Kompatibles System ermittelt (SCD)
- Lösen Sie das folgende System aus drei Gleichungen mit drei Unbekannten mithilfe der Cramer-Regel:
![Rendered by QuickLaTeX.com \begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6013b7e73c89c24fe388f1a5d018f32b_l3.png)
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c710ed86223f47f39b5a25720b5ca19d_l3.png)
Wir berechnen nun den Rang der beiden Matrizen, um zu sehen, um welche Art von System es sich handelt. Um den Rang von A zu berechnen, berechnen wir die 3×3-Determinante der gesamten Matrix (unter Verwendung der Sarrus-Regel) und prüfen, ob sie 0 ergibt:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae4a3bb88d113494463df8e670c326c6_l3.png)
Die Determinante von A ist von 0 verschieden, daher hat die Matrix A den Rang 3.
![]()
Die Matrix A‘ hat also auch den Rang 3 , da sie nicht den Rang 4 haben kann und mindestens den gleichen Rang wie die Matrix A haben muss.
![]()
Die Ausdehnung der Matrix A ist gleich der Ausdehnung der Matrix A‘ und der Anzahl der Unbekannten des Systems (3). Daher wissen wir aufgrund des Rouché-Frobenius-Theorems , dass es sich um ein determiniertes kompatibles System (SCD) handelt:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
Sobald wir wissen, dass das System ein SCD ist, wenden wir die Cramer-Regel an, um es zu lösen. Denken Sie dazu daran, dass die Matrix A, ihre Determinante und die Matrix A‘ sind:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b2b3e5865c2264c360fb887d37a5f6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a604d8f5a3927a47a264d28f7a007b2_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die erste Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1fa494ffb5e452d59c4d2dad40f925a_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die zweite Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08e3dabe2f33434eb96658491f67c0b4_l3.png)
Berechnung
![]()
Mit der Cramer-Regel ändern wir die dritte Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96e76cb8867224755e9c19254678abd4_l3.png)
Die Lösung des Gleichungssystems lautet daher:
![]()
Beispiel 2: Unbestimmtes kompatibles System (ICS)
- Lösen Sie das folgende Gleichungssystem mit der Cramer-Regel:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-781530aac4d8507fd6c7cbd77c3b4651_l3.png)
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a64800a78bf8e2e2f547be907e6863cb_l3.png)
Nun berechnen wir die Reichweite der beiden Matrizen und können so erkennen, um welche Art von System es sich handelt. Um den Rang von A zu berechnen, berechnen wir die Determinante der gesamten Matrix (unter Verwendung der Sarrus-Regel) und prüfen, ob sie 0 ist:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-581c58cbe0fdd9952e7e25b919ecc33b_l3.png)
Die Determinante ergibt 0, daher hat die Matrix A nicht den Rang 3. Sie hat aber eine von 0 verschiedene 2×2-Determinante:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Matrix A hat also Rang 2 :
![]()
Sobald wir die Ausdehnung der Matrix A kennen, berechnen wir die der Matrix A‘. Die Determinante der ersten 3 Spalten ergibt 0, also probieren wir die anderen möglichen 3×3 Determinanten in der Matrix A‘ aus:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-686e7ca635ecee685005f6013c2e64ad_l3.png)
Alle Determinanten der Ordnung 3 ergeben 0. Aber offensichtlich hat die Matrix A‘ die gleiche 2×2-Determinante ungleich 0 wie die Matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Daher hat die Matrix A‘ auch den Rang 2 :
![]()
Da also der Rang der Matrix A gleich dem Rang der Matrix A‘ ist, diese beiden jedoch kleiner sind als die Anzahl der Unbekannten des Systems (3), wissen wir durch den Satz von Rouché-Frobenius , dass es sich um ein unbestimmt kompatibles System handelt (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Wenn wir ein kompatibles unbestimmtes System (SCI) lösen wollen, müssen wir das System transformieren : Zuerst eliminieren wir eine Gleichung, dann konvertieren wir eine Variable in λ (normalerweise die Variable z) und schließlich setzen wir die Terme mit λ zusammen die unabhängigen Begriffe.
Sobald wir das System transformiert haben, wenden wir die Cramer-Regel an und erhalten die Lösung des Systems als Funktion von λ.
In diesem Fall streichen wir die letzte Gleichung aus dem System:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0511fecc9c2af695b6b8eccae6b0661_l3.png)
Nun wandeln wir die Variable z in λ um:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d6142d2be611954fd849a032a97245a_l3.png)
Und wir setzen die Terme mit λ mit den unabhängigen Termen zusammen:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00214205f2334f1c9bc10810c1c1df83_l3.png)
Daher bleiben die Matrix A und die Matrix A‘ des Systems bestehen:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c4b47303973b823a1c5628f5448ca79_l3.png)
Sobald wir das System transformiert haben, wenden wir schließlich die Cramer-Regel an . Wir lösen daher die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b79f52dc82f5cfc311867273e78c06_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die erste Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ff917eaea976c65bd18e0476078d3cb_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die zweite Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-155ca520739bbf7e040a6cdc632f7c27_l3.png)
Während die Lösung des Gleichungssystems eine Funktion von λ ist, da es ein SCI ist und daher unendlich viele Lösungen hat:
![]()
Cramers Regel löste Probleme
Übung 1
Wenden Sie die Cramer-Regel an, um das folgende System aus zwei Gleichungen mit zwei Unbekannten zu lösen:
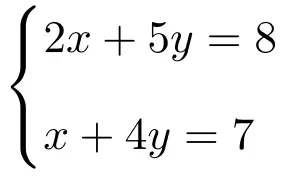
Als erstes müssen die Matrix A und die erweiterte Matrix A‘ des Systems erstellt werden:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a001db9cf56846150730fee7126dacd_l3.png)
Wir müssen nun den Rang der Matrix A ermitteln. Dazu prüfen wir, ob die Determinante der gesamten Matrix von 0 verschieden ist:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c75c1c344c286016bea83237f1f418e_l3.png)
Da die Matrix eine von 0 verschiedene 2×2-Determinante hat, hat die Matrix A Rang 2:
![]()
Sobald wir den Rang von A kennen, berechnen wir den Rang von A‘. Dies wird mindestens Rang 2 sein, da wir gerade gesehen haben, dass es eine von 0 verschiedene Determinante der Ordnung 2 enthält. Darüber hinaus kann es nicht Rang 3 sein, da wir keine 3×3-Determinante erstellen können. Daher hat die Matrix A‘ auch den Rang 2:
![]()
Daher wissen wir durch die Anwendung des Rouché-Frobenius-Theorems, dass es sich um ein kompatibles Determinantensystem (SCD) handelt, da der Bereich von A gleich dem Bereich von A‘ und der Anzahl der Unbekannten ist.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbd67b16bb6d52a0696e70a77833cd3b_l3.png)
Sobald wir wissen, dass das System ein SCD ist, wenden wir die Cramer-Regel an, um es zu lösen.
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die erste Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0adeda8f2ce557661466996038b1148_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die zweite Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-59790a66cc31fac07be1d5a7bb556d9e_l3.png)
Die Lösung des Gleichungssystems lautet daher:
![]()
Übung 2
Finden Sie die Lösung des folgenden Systems aus drei Gleichungen mit drei Unbekannten mithilfe der Cramer-Regel:
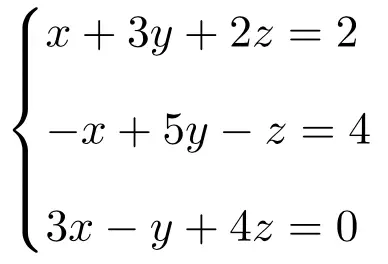
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-eea75fbf6d86ebc3d0b9e236cd2160f5_l3.png)
Wir ermitteln nun den Rang der Matrix A, indem wir die Determinante der 3×3-Matrix mit der Sarrus-Regel berechnen:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73f751f3b5c527c16b5de1b10bf07a4e_l3.png)
Die Matrix hat eine von 0 verschiedene Determinante der Ordnung 3, die Matrix A hat den Rang 3:
![]()
folglich hat die Matrix A‘ auch den Rang 3:
![]()
Mithilfe des Satzes von Rouché-Frobenius wissen wir daher, dass es sich um ein kompatibles Determinantensystem (SCD) handelt, da der Bereich von A gleich dem Bereich von A‘ und der Anzahl der Unbekannten ist.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Sobald wir wissen, dass das System ein SCD ist, müssen wir die Cramer-Regel anwenden, um das System zu lösen.
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die erste Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc574297f609b68e4fb48466ec6c8077_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die zweite Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2544601137d62e217ff1866f278203d6_l3.png)
Berechnung
![]()
Mit der Cramer-Regel ändern wir die dritte Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42d7d4adcfc48954185ca14b56b8e128_l3.png)
Die Lösung des Gleichungssystems lautet daher:
![]()
Übung 3
Berechnen Sie die Lösung des folgenden Systems aus drei Gleichungen mit drei Unbekannten mithilfe der Cramer-Regel:
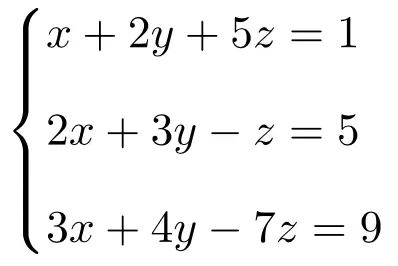
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-afd359275e5ebaaf3229504c47a5815f_l3.png)
Wir berechnen den Umfang der Matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ddf17a2b3eed5a680d685900a79b31_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdd4380c7c76418bd3ec12c94359f886_l3.png)
![]()
Sobald wir die Ausdehnung der Matrix A kennen, berechnen wir die der Matrix A‘. Die Determinante der ersten 3 Spalten ergibt 0, also probieren wir die anderen möglichen 3×3 Determinanten in der Matrix A‘ aus:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-1addc62130e0462075b3bade26a7e35e_l3.png)
Alle Determinanten der Ordnung 3 ergeben 0. Die Matrix A‘ hat jedoch die gleiche 2×2 Nicht-0-Determinante wie die Matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-7de377466bd5afd03f58f9b532324e75_l3.png)
Daher hat die Matrix A‘ auch den Rang 2:
![]()
Da der Rang der Matrix A gleich dem Rang der Matrix A‘ ist, diese beiden jedoch kleiner sind als die Anzahl der Unbekannten des Systems (3), wissen wir anhand des Rouché-Frobenius-Theorems , dass es sich um ein unbestimmt kompatibles System (ICS) handelt:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Da wir ein ICS-System sind, müssen wir eine Gleichung beseitigen. In diesem Fall streichen wir die letzte Gleichung aus dem System:
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a1d067e155540f4345cf56e5c1567d3_l3.png)
Nun wandeln wir die Variable z in λ um:
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5fa91777a722d3783b2f887aab44152_l3.png)
Und wir setzen die Terme mit λ mit den unabhängigen Termen zusammen:
![Rendered by QuickLaTeX.com \begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76ff21181be050b01c247981298986a7_l3.png)
So dass die Matrix A und die Matrix A‘ des Systems bestehen bleiben:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-230e5b28dd467127e63f4f9756cf90da_l3.png)
Sobald wir das System transformiert haben, wenden wir schließlich die Cramer-Regel an . Wir lösen daher die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1](https://mathority.org/wp-content/ql-cache/quicklatex.com-f127efbd217e2bca8852ec792610732f_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die erste Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42652a14362b42e606841b6bb3e77cc0_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die zweite Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b95c5870f1762a2d82c9ebcccbca7408_l3.png)
Während die Lösung des Gleichungssystems eine Funktion von λ ist, da es ein SCI ist und daher unendlich viele Lösungen hat:
![]()
Übung 4
Lösen Sie das folgende Problem eines Systems aus drei Gleichungen mit drei Unbekannten, indem Sie die Cramer-Regel anwenden:
![Rendered by QuickLaTeX.com \begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e1c3458f33b863db10750b9e51d09e_l3.png)
Zuerst konstruieren wir die Matrix A und die erweiterte Matrix A‘ des Systems:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-743a40010cb4a610e8a3fc6ae5d313b4_l3.png)
Berechnen wir nun den Rang der Matrix A, indem wir die Determinante der 3×3-Matrix mithilfe der Sarrus-Regel berechnen:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-713c634fbc3e1b1cb228e3891c9bff1c_l3.png)
Die Matrix hat eine von 0 verschiedene Determinante der Ordnung 3, die Matrix A hat den Rang 3:
![]()
Folglich hat die Matrix A‘ auch den Rang 3, da sie mindestens den gleichen Rang wie die Matrix A haben muss, und sie kann nicht den Rang 4 haben, da es sich um eine Matrix der Dimension 3×4 handelt.
![]()
Daher folgern wir mithilfe des Rouché-Frobenius-Theorems, dass es sich um ein determiniertes kompatibles System (SCD) handelt, da der Bereich von A gleich dem Bereich von A‘ und der Anzahl der Unbekannten ist.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Sobald wir wissen, dass das System ein SCD ist, müssen wir die Cramer-Regel anwenden, um das System zu lösen.
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die erste Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a290479c69ff806f19dcf29f96e1228_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die zweite Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bba0765fbcbcebf0585520af25b4a30_l3.png)
Berechnung
![]()
Mit der Cramer-Regel ändern wir die dritte Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bc157a8c4dfe8ee4651affac68ef878_l3.png)
Die Lösung des linearen Gleichungssystems lautet daher:
![]()
Übung 5
Lösen Sie das folgende lineare Gleichungssystem mit der Cramer-Regel:
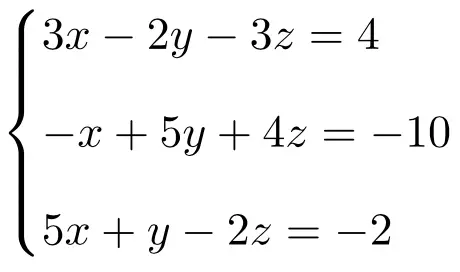
Wir erstellen zunächst die Matrix A und die erweiterte Matrix A‘ des Systems:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5153b5951b768cc3cafa2bb2567ba92_l3.png)
Wir berechnen den Umfang der Matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3778c9499e2a44ea3834dfed1523163_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03d70742b14ced92f33963df0c86e92f_l3.png)
![]()
Sobald wir die Ausdehnung der Matrix A kennen, berechnen wir die der Matrix A‘. Die Determinante der ersten 3 Spalten ergibt 0, also probieren wir die anderen möglichen 3×3 Determinanten in der Matrix A‘ aus:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bed93d532ae4ccd4649a73662f55f0f_l3.png)
Alle Determinanten der Ordnung 3 ergeben 0. Aber offensichtlich hat die Matrix A‘ die gleiche Determinante der Ordnung 2 außer 0 wie die Matrix A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-858d95d7d252b16706b66c0e6aba09c4_l3.png)
Daher hat die Matrix A‘ auch den Rang 2:
![]()
Der Rang der Matrix A ist gleich dem Rang der Matrix A‘, aber diese beiden sind kleiner als die Anzahl der Unbekannten des Systems (3), sodass wir anhand des Rouché-Frobenius-Theorems wissen, dass es sich um ein unbestimmtes kompatibles System (SCI) handelt. :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Da es sich um ein ICS-System handelt, müssen wir eine Gleichung eliminieren. In diesem Fall streichen wir die letzte Gleichung aus dem System:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e10bd826663dff41c4272610cbc07b1_l3.png)
Nun wandeln wir die Variable z in λ um:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2502be450040b38761c08e5d6beaf379_l3.png)
Und wir setzen die Terme mit λ mit den unabhängigen Termen zusammen:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80a43d98e6be30965d554e8a89aa5d89_l3.png)
So dass die Matrix A und die Matrix A‘ des Systems bestehen bleiben:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3451ce571163983cf41794d4998283d6_l3.png)
Sobald wir das System transformiert haben, wenden wir schließlich die Cramer-Regel an . Wir lösen daher die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e7a7d6208ea5e762f5c74a44e6838cf_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die erste Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8c30fcc0526c2d4112eb4f60a3d8847f_l3.png)
Um das Unbekannte zu berechnen
![]()
Mit der Cramer-Regel ändern wir die zweite Spalte der Determinante von A durch die Spalte der unabhängigen Terme und dividieren sie durch die Determinante von A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdb22a54274e019c811c9051502c474a_l3.png)
Somit ist die Lösung des Gleichungssystems eine Funktion von λ, da es ein SCI ist und das System daher unendlich viele Lösungen hat:
![]()