Haben Sie sich jemals gefragt, wie sich rationale Zahlen von anderen Zahlen unterscheiden? In diesem Artikel werden wir rationale Zahlen eingehend untersuchen, einschließlich ihrer einzigartigen Eigenschaften und Klassifizierung. Machen Sie sich bereit, das Konzept besser zu verstehen!
Was sind rationale Zahlen?
Rationale Zahlen (ℚ) sind eine Unterklasse der reellen Zahlen , die alle Zahlen umfasst, die als Bruch ausgedrückt werden können. Dies bedeutet, dass rationale Zahlen diejenigen sind, die als Verhältnis zweier ganzen Zahlen a/b geschrieben werden können, wobei b ≠ 0 ist.
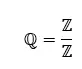
Rationale Zahlen können auch als wiederholte oder endliche Dezimalzahlen ausgedrückt werden, da sie aus einer Reihe wiederholter Ziffern bestehen. Einige Beispiele für rationale Zahlen sind 1/2, 3/4, 10/3, 2/3 und π (pi).
Teilmengen von Rationalen
Rationale Zahlen können in zwei Teilmengen unterteilt werden:
- Ganze Zahlen , zu denen 0, alle natürlichen Zahlen und alle negativen Zahlen gehören.
- Dezimalzahlen oder Bruchzahlen , das sind alle Zahlen, die Werte ausdrücken, die aus einem ganzzahligen Teil und einem Dezimalteil bestehen. Letzterer ermöglicht die Darstellung von Werten kleiner als Eins.

Eine weitere Unterkategorie der Menge der reellen Zahlen sind die irrationalen Zahlen , die etwas komplexer sind.
Beispiele für rationale Zahlen
Rationale Zahlen sind solche, die sich als Bruch, also als Quotient zweier ganzer Zahlen, ausdrücken lassen. Hier sind einige Beispiele für rationale Zahlen:
-23
-4/5
-1/2
-7/9
Alle Brüche, die eine ganze Zahl darstellen, sind gleichermaßen rational. Zum Beispiel:
-1/1
-2/2
-3/3
Eigenschaften rationaler Zahlen
Das Hauptmerkmal rationaler Zahlen ist, dass sie immer einen Nenner ungleich Null haben.
Die zweite Eigenschaft dieser Menge besteht darin, dass jede rationale Zahl durch unendlich viele äquivalente Brüche dargestellt werden kann. Beispielsweise kann die rationale Zahl 3,5, die 7/2 entspricht, auch als 14/4, 28/8… und als unendlich viele andere Brüche geschrieben werden.
Rationale Zahlen erfüllen auch die Verteilungseigenschaft . Das bedeutet, dass die Multiplikation oder Division eines Bruchs mit einem anderen keinen Einfluss auf das Ergebnis hat:
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
Darstellung rationaler Zahlen
Rationale Zahlen können auf verschiedene Arten dargestellt werden, die gebräuchlichste ist jedoch die Darstellung als Bruch . Ein Bruch besteht aus zwei Zahlen: dem Zähler und dem Nenner.
Der Zähler gibt an, wie viele Teile des Ganzen betrachtet werden, während der Nenner angibt, wie viele gleiche Teile im Ganzen sind. Wenn beispielsweise ein Kuchen in acht gleiche Stücke geteilt wird und drei dieser Stücke gegessen werden, beträgt der Bruchteil, der die Menge des gegessenen Kuchens darstellt, 3/8.
Eine andere Möglichkeit, rationale Zahlen darzustellen, sind Dezimalzahlen . Dezimalzahlen sind eine Abkürzung für einen Bruch, bei dem der Nenner eine Zahl von 10, 100, 1000 usw. ist. Wenn Sie beispielsweise 1/4 eines Kuchens haben, kann dies als 0,25 ausgedrückt werden (was „0 Ganzes und 25/100“ bedeutet).
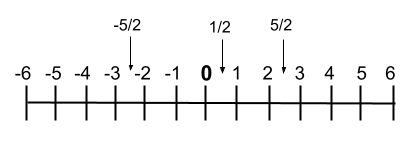
Wenn wir sie jedoch grafisch darstellen wollen, können wir sie auch auf den Zahlenstrahl schreiben, in dem man die Reihenfolge der Zahlen sehr gut erkennen kann. Als nächstes zeigen wir Ihnen ein Beispiel dieser Zeile :
Rationale Operationen
Die grundlegenden Operationen rationaler Zahlen sind die gleichen wie die der ganzen Zahlen: Addition, Subtraktion, Multiplikation und Division. Wenn Sie erfahren möchten, wie Sie diese Art von Operationen lösen können, empfehlen wir Ihnen, unseren Artikel über Operationen mit Brüchen zu lesen.
Wenn Sie jedoch mit rationalen Zahlen auf Dezimalbasis arbeiten, müssen Sie die Vorgehensweise zum Lösen von Operationen befolgen, die Sie beim Umgang mit Dezimalwerten verwenden.
Fazit zur Menge der rationalen Zahlen
Nach dieser ausführlichen Erklärung können wir schlussfolgern, dass die Menge der rationalen Zahlen eine der wichtigsten in der Mathematik ist. Es enthält alle Zahlen, die sich als Bruch darstellen lassen, wodurch wir Mengen sehr präzise ausdrücken können.