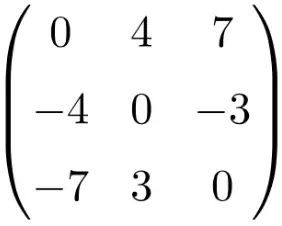Quadratische Matrix

Auf dieser Seite erklären wir, was eine quadratische Matrix ist und Sie finden Beispiele für quadratische Matrizen. Darüber hinaus erfahren Sie, welche Eigenschaften quadratische Matrizen haben, welche Operationen mit ihnen durchgeführt werden können und welche verschiedenen Typen es gibt.

Was ist eine quadratische Matrix?

Eine quadratische Matrix ist a Matrix, die die gleiche Anzahl an Zeilen wie Spalten hat.

Beispiele für quadratische Matrizen

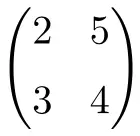
quadratische Matrix der Ordnung 2

Beispiel einer quadratischen Matrix der Ordnung 2

quadratische Matrix der Ordnung 3

Beispiel einer quadratischen Matrix der Ordnung 3

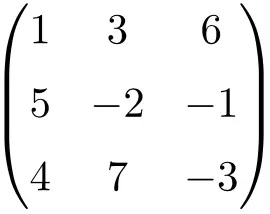
quadratische Matrix der Ordnung 4

Beispiel einer quadratischen Matrix der Ordnung 4

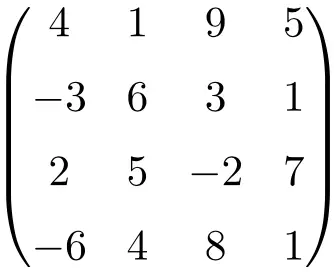
Wie Sie sehen, werden quadratische Matrizen normalerweise nach ihrer Ordnung benannt, d. h. eine quadratische Matrix der Ordnung 2 bedeutet, dass es sich um eine Matrix der Dimension 2×2 (2 Zeilen und 2 Spalten) handelt, oder wir sprechen von einer quadratischen Matrix der Ordnung 3 was darauf hinweist, dass es eine Größe von 3×3 (3 Zeilen und 3 Spalten) hat.

Diagonalen einer quadratischen Matrix

Die Diagonalen quadratischer Matrizen haben bestimmte Namen, es gibt die Hauptdiagonale und die Nebendiagonale:

Die Hauptdiagonale einer quadratischen Matrix besteht aus den Elementen, die von der oberen linken Ecke zur unteren rechten Ecke verlaufen:

Hauptdiagonale einer quadratischen Matrix

Die sekundäre Diagonale einer quadratischen Matrix entspricht den Elementen, die von der unteren linken Ecke zur oberen rechten Ecke verlaufen:

Sekundärdiagonale einer quadratischen Matrix

Eigenschaften einer quadratischen Matrix

Quadratische Matrizen werden in der linearen Algebra häufig verwendet und sind daher so wichtig. Sehen wir uns also an, welche Merkmale diese Matrizenklasse so relevant machen:

Jede quadratische Matrix kann in eine Summe aus einer symmetrischen Matrix und einer antisymmetrischen Matrix zerlegt werden.

Wenn zwei quadratische Matrizen die gleiche Ordnung haben, können sie voneinander addiert oder subtrahiert werden:

$\begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}$

Zwei quadratische Matrizen können in beide möglichen Richtungen multipliziert werden . Allerdings ist das Produkt quadratischer Matrizen nicht kommutativ, d. h. das Ergebnis der Multiplikation ändert sich je nachdem, mit welcher Seite es multipliziert wird. Beachten Sie im folgenden Beispiel, wie das Ergebnis von den Positionen der Matrizen abhängt:

$\begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}$

$\begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}$

Quadratische Matrizen sind die einzigen, die die Determinante berechnen können. Daher kann eine Determinante nur gelöst werden, wenn es sich um eine quadratische Matrix handelt. Um beispielsweise die Determinante einer quadratischen 3×3-Matrix zu ermitteln, müssen Sie die Regel von Sarrus anwenden:

$\displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}$

Denken Sie auch daran, dass, wenn die Determinante der Matrix von 0 verschieden ist, dies bedeutet, dass es sich um eine reguläre Matrix handelt, das heißt, sie ist invertierbar. Wenn andererseits die Determinante Null ist, handelt es sich um eine singuläre Matrix (die keine Umkehrung hat).

Schließlich können quadratische Matrizen diagonalisiert werden . Somit kann ein Basiswechsel durchgeführt werden, um die Eigenwerte (oder Eigenwerte) und die Eigenvektoren (oder Eigenvektoren) einer quadratischen Matrix zu berechnen.

Operationen mit quadratischen Matrizen

Wie wir gesehen haben, kann die Determinante einer Matrix nur berechnet werden, wenn die Matrix quadratisch ist. Ebenso gibt es bestimmte Operationen, die nur ausgeführt werden können, wenn die Matrix eine quadratische Dimension hat:

Spur einer Matrix

Die Spur einer Matrix ist die Summe der Elemente, die die Hauptdiagonale einer quadratischen Matrix bilden.

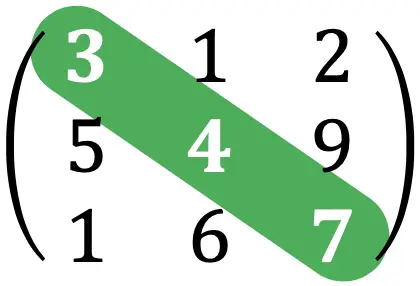
Die Spur der Matrix aus der obigen Übung wäre beispielsweise:

$\text{tr}(A)=3+4+7=\bm{14}$

Arten von quadratischen Matrizen

Dann haben Sie die wichtigsten Arten quadratischer Matrizen, die es gibt. Klicken Sie auf den Matrizentyp, um herauszufinden, was ihn besonders macht.