Quadrat einer Summe (oder Summe im Quadrat)

Auf dieser Seite finden Sie die Formel für das Quadrat einer Summe, also der notenbaren Identität (a+b) ² . Außerdem können Sie sich Beispiele und gelöste Übungen zum Thema Quadratsummen ansehen. Und darüber hinaus werden Sie die geometrischen Eigenschaften entdecken, die in diesem bemerkenswerten Produkt verborgen sind.

Was ist das Quadrat einer Summe?

Das Quadrat einer Summe ist eine der bemerkenswerten Identitäten (oder bemerkenswerten Produkte), es handelt sich also um eine mathematische Regel, mit der Sie schnell die Potenz eines Binomials mit zwei quadrierten positiven Termen berechnen können.

Somit besteht das Quadrat einer Summe aus zwei verschiedenen Termen, die addiert und quadriert werden, d. h. der algebraische Ausdruck für das Quadrat einer Summe ist (a+b) ² .

Formel für das Quadrat einer Summe

Angesichts der mathematischen Definition dieser bemerkenswerten Art von Identität werden wir nun sehen, wie die Formel für das Quadrat einer Summe lautet:

Damit ist das Quadrat einer Summe gleich dem Quadrat des ersten Termes plus dem doppelten Produkt des ersten mit dem zweiten plus dem Quadrat des zweiten.

Um eine quadrierte Summe zu lösen, reicht es also nicht aus, jede Addition auf zwei zu erhöhen, sondern zusätzlich müssen die beiden Additionen miteinander und mit 2 multipliziert werden.

Dies ist wichtig zu beachten, da ein sehr häufiger Fehler beim Addieren der Quadrate darin besteht, das Produkt zwischen den beiden Termen zu vergessen und nur die Quadrate zu berechnen:

Denken Sie daran, keine Begriffe aus der Formel wegzulassen!

Denken Sie andererseits daran, dass die Formel für eine quadrierte Subtraktion (oder das Quadrat einer Subtraktion) der gerade gesehenen sehr ähnlich ist, aber einen Unterschied aufweist, der das Ergebnis völlig verändert. Wenn Sie nicht sicher sind, wie das aussieht, können Sie hier nachsehen, was die quadrierte Subtraktionsformel ist und wie sie angewendet wird.

Beispiele für Summenquadrate

Hier sind einige praktische Beispiele, damit Sie sehen können, wie man eine Summe quadriert:

Beispiel 1

Berechnen Sie die folgende Quadratsumme, indem Sie die Formel anwenden:

$(x+5)^2$

Die Formel für eine quadrierte Summe lautet:

$(a+b)^2=a^2+2ab+b^2$

Wir müssen zunächst die Parameter identifizieren

$a$

Und

$b$

der Formel. In diesem Fall,

$a$

repräsentiert die

$x$

des Paares und

$b$

entsprechen Nummer 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Nun, da wir jetzt die Werte kennen

$a$

und von

$b,$

Wir können die Formel anwenden, um das Ergebnis des Quadrats der Summe zu ermitteln:

Quadrat einer Summe bemerkenswerter Produkte

Beispiel 2

Lösen Sie den folgenden Ausdruck nach dem Quadrat einer Summe auf:

$(3x+4)^2$

Die Formel für das Quadrat einer Summe lautet:

$(a+b)^2=a^2+2ab+b^2$

Also in diesem Problem

$a$

ist das Monom

$3x$

Und andererseits,

$b$

ist der unabhängige Term 4:

$\begin{array}{c} a=3x \\[2ex] b=4 \end{array}$

Sobald wir endlich die Werte von identifiziert haben

$a$

und von

$b$

, wenden wir die Quadratsummenformel an, um das bemerkenswerte Produkt zu lösen:

$\begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}$

Beweis der Formel für das Quadrat einer Summe

Dann werden wir die Formel, die wir gerade gesehen haben, aus dem Quadrat einer Summe ableiten, damit Sie verstehen, woher sie kommt.

Ausgehend von einem auf 2 angehobenen positiven Binomial:

$(a+b)^2$

Die obige Potenz entspricht offensichtlich dem Faktor

$(a+b)$

mit sich selbst multipliziert:

$(a+b)^2=(a+b)\cdot (a+b)$

Also multiplizieren wir die beiden Klammern mit der Verteilungseigenschaft:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Abschließend gruppieren wir aus den resultierenden Begriffen diejenigen, die ähnlich sind:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

Und wir sind bereits beim polynomialen Ausdruck der Formel angekommen, also ist es bewiesen:

$(a+b)^2= a^2+2ab+b^2$

Obwohl man es kaum glauben mag, funktioniert die Quadrat-Summenformel auch für die Faktorisierung quadratischer Polynome . Falls Sie nicht wissen, was es ist: Polynomfaktorisierung ist ein Verfahren, das in der Mathematik häufig verwendet wird, um den Ausdruck eines Polynoms zu vereinfachen. Erfahren Sie, wie es geht, indem Sie auf den Link oben klicken.

Geometrische Interpretation des Quadrats einer Summe

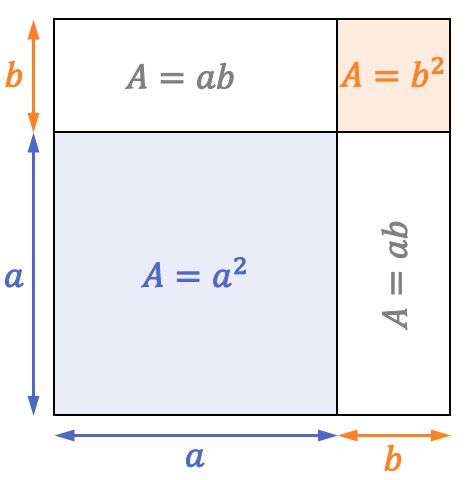
Bisher haben wir gesehen, wie das Quadrat einer Summe mathematisch berechnet wird, aber dieses bemerkenswerte Produkt kann auch geometrisch interpretiert werden.

Schauen Sie sich das folgende Quadrat an, dessen Seiten messen

$a+b:$

quadratische geometrische Interpretation einer Summe

Die Fläche eines Quadrats ist gleich der Länge einer seiner Seiten im Quadrat. Daher wie die Seite des vorherigen Quadrats ist

$a+b,$

seine Fläche (oder Oberfläche) ist gleich

$(a+b)^2.$

Nun, wie Sie in der quadratischen Darstellung sehen können, ein Quadrat mit einer Fläche von

$a^2,$

Rechtecke mit zwei Flächen

$ab,$

und ein weiteres Quadrat der Oberfläche

$b^2.$

Daher ist die Formel für die Summe eines Quadrats auch aus geometrischer Sicht erfüllt:

$(a+b)^2=a^2+2ab+b^2$

Probleme des Quadrats einer Summe gelöst

Dann überlassen wir Ihnen Schritt für Schritt mehrere gelöste Quadratsummenübungen, damit Sie üben und so das Konzept vollständig verstehen können. Sie können uns alle Ihre Fragen in den Kommentaren schreiben, wir beantworten sie gerne. 💭💭💭

Übung 1

Bestimmen Sie die folgenden Summen im Quadrat:

$\text{A)} \ (x+3)^2$

$\text{B)} \ (2+6x)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

siehe Lösung

Um alle wesentlichen Identitäten des Problems zu lösen, reicht es aus, die Formel für das Quadrat einer Summe anzuwenden:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Übung 2

Lösen Sie die folgenden Summenquadrate zweier Terme, indem Sie die Formel anwenden:

$\text{A)} \ \left(4x^2+2y^3\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}+\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

siehe Lösung

Um alle nennenswerten Produkte des Problems zu berechnen, müssen Sie die Formel für eine quadrierte Summe verwenden:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

In Abschnitt B) müssen Sie bedenken, dass das Quadratieren einer Wurzel vereinfacht wird:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}$

Die Monome des letzten Summenquadrats haben Bruchkoeffizienten, daher müssen wir zur Lösung auch die Eigenschaften von Brüchen verwenden:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

Übung 3

Finden Sie die folgende Potenz, indem Sie die Formel für das Quadrat einer Summe anwenden, ohne den Taschenrechner zu verwenden:

$17^2$

siehe Lösung

Zunächst lässt sich die Zahl siebzehn in die Summe von 10 plus 7 zerlegen:

$17^2=(10+7)^2$

Also haben wir die Potenz in eine quadrierte Summe umgewandelt. Daher können wir nun die entsprechende Formel anwenden:

$\begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}$

Kurz gesagt ist das Ergebnis der Potenzierung:

$17^2=\bm{289}$

Wie Sie in dieser Übung gesehen haben, ist die Summenquadratformel auch nützlich, um Potenzen großer Zahlen zu berechnen, ohne einen Taschenrechner zu verwenden.

Quadrat einer Summe von 3 Termen

Manchmal stellen wir möglicherweise fest, dass wir das Quadrat von drei addierten Termen lösen müssen, z. B. (a+b+c) ² . Logischerweise können wir in diesen Fällen die von uns erläuterte Formel nicht verwenden, da wir in den Klammern ein Trinom anstelle eines Binomials haben. Daher muss eine andere Formel verwendet werden.

Die Formel für das Quadrat der Summe von 3 Termen lautet wie folgt:

$\definecolor{blauquadreejemplo}{HTML}{ff5733} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=blauquadreejemplo, boxrule=1.2pt, boxsep=2.5mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2.5mm}{-2.5mm}{0mm}{blauquadreejemplo!20!white,} ]}]{equation*} (a+b+c)^2 = a^2+2a(b+c)+b^2+2bc+c^2 \end{empheq}$

Sehen wir uns anhand eines Beispiels an, wie diese Formel angewendet wird:

$\begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}$

Wie Sie sehen, wird das Ergebnis durch das Hinzufügen eines Elements zur Formel viel komplizierter.

Quadrat einer summe (oder summe im quadrat)

Was ist das Quadrat einer Summe?

Formel für das Quadrat einer Summe

Beispiele für Summenquadrate

Beispiel 1

Beispiel 2

Beweis der Formel für das Quadrat einer Summe

Geometrische Interpretation des Quadrats einer Summe

Probleme des Quadrats einer Summe gelöst

Übung 1

Übung 2

Übung 3

Quadrat einer Summe von 3 Termen

Kommentar verfassen Kommentieren abbrechen