Quadrat einer differenz (oder subtraktion)

Hier erklären wir, was die bemerkenswerte Identitätsformel des Quadrats einer Differenz (oder Subtraktion) ist, das heißt, wir zeigen Ihnen, wie der Ausdruck (ab) ² gelöst wird. Darüber hinaus können Sie Beispiele sehen und mit Übungen üben, die zum Quadrat der Differenz gelöst werden. Und schließlich zeigen wir die Formeldemonstration und geometrische Interpretation dieses bemerkenswerten Produkttyps.

Was ist das Quadrat einer Differenz (oder Subtraktion)?

Das Quadrat einer Differenz oder das Quadrat einer Subtraktion ist eine der bemerkenswerten Identitäten (oder bemerkenswerten Produkte), das heißt, es besteht aus einer mathematischen Regel, die die Berechnung der Quadratur eines Binomials mit zwei Termen erleichtert: einem positiven und das andere negativ.

Daher ist der algebraische Ausdruck für das Quadrat einer Differenz (ab) ² .

Formel für das Quadrat einer Differenz (oder Subtraktion)

Sobald wir die Definition dieser Art bemerkenswerter Identität gesehen haben, werden wir sehen, wie man das Quadrat einer Differenz mit ihrer Formel löst:

Damit ist das Quadrat einer Differenz gleich dem Quadrat des ersten Termes, minus dem doppelten Produkt des ersten mit dem zweiten, plus dem Quadrat des zweiten.

Um also eine Differenz oder eine quadrierte Subtraktion zu berechnen, müssen Sie nicht nur jeden Term auf zwei erhöhen, sondern sie auch miteinander und mit 2 multiplizieren.

Dies ist wichtig zu beachten, da ein sehr häufiger Fehler beim Subtrahieren von Quadraten darin besteht, nicht das Produkt zwischen den beiden Termen zu bilden und nur das Quadrat der Abnahme und die Subtraktion der Subtraktion zu lösen:

Vergessen Sie nicht das Produkt zwischen a und b!

Beispiele für Differenzquadrate (oder Subtraktionsquadrate).

Da wir nun die Formel für das Quadrat einer Differenz kennen, können wir damit Berechnungen durchführen. Und damit Sie sehen können, wie das geht, haben wir mehrere gelöste Beispiele für das Quadrat einer Differenz (oder Subtraktion) vorbereitet.

Beispiel 1

• Lösen Sie die folgende Differenz im Quadrat:

Da es sich um eine quadrierte Subtraktion handelt, müssen Sie die Formel anwenden:

Wir müssen also die Werte der Unbekannten ermitteln

Und

der Formel. In diesem Fall,

ist die Variable

Und

entsprechen Nummer 3:

Beachten Sie, dass das negative Vorzeichen nicht Teil von ist

Sie müssen jedoch immer die Zahl ohne Vorzeichen nehmen, um die Formel richtig anzuwenden.

Wir kennen daher bereits die Werte von

und von

Daher müssen wir nur diese Werte in die Formel einsetzen:

Beispiel 2

• Berechnen Sie das folgende Binomial einer quadrierten Subtraktion:

Die Formel für die quadrierte Differenz lautet:

Wir müssen also zunächst die Werte von identifizieren

und von

der Formel. Bei diesem Problem gilt:

stellt das Monom dar

Und

ist äquivalent zum unabhängigen Term des Binomials, also 2:

Schließlich kennen wir den Wert der Parameter

Und

, wenden wir einfach die Binomialformel für die quadrierte Subtraktion an:

Beweis der Formel für das Quadrat einer Differenz

Wir werden dann ableiten, woher die Formel für das Quadrat einer Subtraktion kommt. Obwohl Sie sich den Beweis nicht merken müssen, ist es dennoch schön, die Mathematik dahinter zu verstehen.

Wenn wir vom Ausdruck des Binomials aller Subtraktionen ausgehen:

Offensichtlich ist die vorherige Potenz gleich dem Produkt des Faktors

mit sich selbst multipliziert:

Jetzt multiplizieren wir die beiden Klammern, indem wir die Verteilungseigenschaft anwenden:

Und wir müssen nur noch ähnliche Begriffe zusammenfassen, um den Beweis der Formel abzuschließen:

Damit die Formel für das Quadrat einer Subtraktion mathematisch bewiesen werden kann:

Kurioserweise wird die Entwicklung des Binomialausdrucks einer quadrierten Subtraktion auch als perfektes quadratisches Trinom bezeichnet.

Geometrische Interpretation des Quadrats einer Differenz

Um den Begriff des Quadrats einer Differenz vollständig zu verstehen, werden wir sehen, wie wir diese bemerkenswerte Gleichheit geometrisch interpretieren können.

Schauen Sie sich das folgende Quadrat mit Seitenlänge an

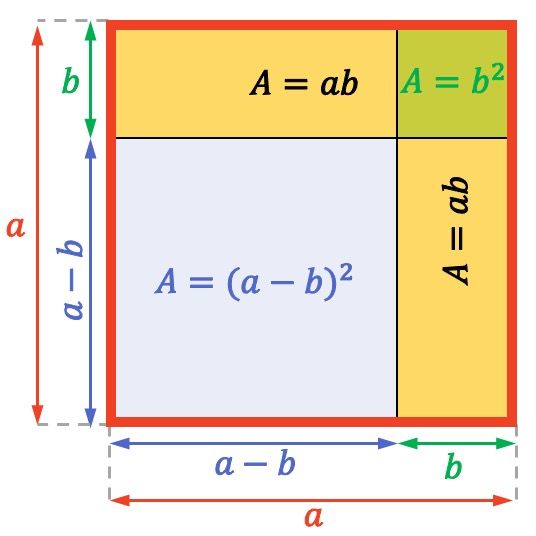
Die Fläche (oder Oberfläche) eines Quadrats oder Rechtecks wird durch Multiplikation zweier benachbarter Seiten berechnet. Daher beträgt die Fläche des gesamten ganzzahligen Quadrats oben

Ebenso ist die Fläche jedes gelben Rechtecks gleich

Und schließlich hat das kleine Quadrat oben rechts eine Fläche von

Dies bedeutet, dass ein Quadrat eine Seite hat

deren Oberfläche ist

kann in die Fläche eines Dimensionsquadrats zerlegt werden

minus 2 mal die Fläche eines Rechtecks mit Abmessungen

Und

, plus der Fläche eines Seitenquadrats

Kurz gesagt, die Formel für das Quadrat einer Differenz lässt sich auch geometrisch verifizieren:

Gelöste Probleme des Quadrats einer Differenz (oder Subtraktion)

Damit Sie üben können, stellen wir Ihnen mehrere Übungen zur Verfügung, die Schritt für Schritt zum bemerkenswerten Produkt des Quadrats einer Differenz gelöst werden. Denken Sie daran, dass Sie uns alle Fragen, die Sie haben, unten in den Kommentaren schreiben können.

Übung 1

Lösen Sie die folgenden Subtraktionen im Quadrat:

Um alle bemerkenswerten Identitäten des Problems zu finden, reicht es aus, die Formel für das Quadrat einer Differenz anzuwenden, die lautet:

Übung 2

Bestimmen Sie die folgenden Quadrate der Differenzen zweier Größen, indem Sie die Formel anwenden:

Um alle nennenswerten Produkte des Problems zu bestimmen, muss die Formel für eine quadrierte Subtraktion verwendet werden:

Um Abschnitt B) zu lösen, müssen Sie bedenken, dass das Quadratieren einer Wurzel vereinfacht wird:

Die Monome der letzten quadrierten Subtraktion haben Bruchkoeffizienten, daher müssen wir zur Lösung die Eigenschaften von Brüchen verwenden: