Auf dieser Seite wird erklärt, wie man einen Vektor numerisch und grafisch mit einer reellen Zahl (oder einem Skalar) multipliziert. Darüber hinaus finden Sie auch Beispiele und gelöste Aufgaben zum Produkt eines Vektors mit einem Skalar. Abschließend werden auch die Eigenschaften dieser Art der Operation mit Vektoren erläutert.
Wie multipliziert man einen Vektor mit einer reellen Zahl?
Um das Produkt eines Vektors und einer Zahl (oder eines Skalars) numerisch zu berechnen, muss jede Komponente des Vektors mit der Zahl multipliziert werden.
![]()
![]()
Somit ergibt das Ergebnis der Multiplikation eines Vektors mit einer Zahl einen neuen Vektor mit den folgenden Eigenschaften:
- Das Ergebnis des Produkts eines Vektors mit einem Skalar ergibt einen neuen Vektor mit derselben Richtung wie der ursprüngliche Vektor.
- Außerdem hat der neue Vektor die gleiche Richtung, wenn die Zahl positiv ist.
- Oder es hat die gegenteilige Bedeutung, wenn die Zahl negativ ist.
- Der Betrag des resultierenden Vektors entspricht dem Betrag des ursprünglichen Vektors multipliziert mit dem Skalar.
In der folgenden Grafik können Sie sehen, wie die Richtung des Vektors unabhängig vom Vorzeichen des Skalars beibehalten wird. Andererseits hängt die Richtung des Vektors vom Vorzeichen der Zahl ab, die er multipliziert.

Darüber hinaus ist in der folgenden Grafik deutlich zu erkennen, dass der Betrag des resultierenden Produktvektors gleich dem Betrag des ursprünglichen Vektors multipliziert mit dem Skalar ist.
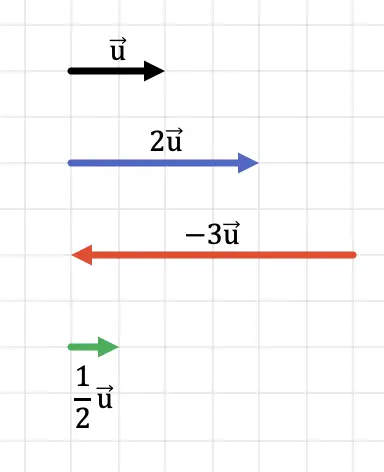
Wenn wir den Vektor mit einer Zahl größer als 1 multiplizieren, ist das Ergebnis offensichtlich ein Vektor mit größerer Länge (mit größerem Modul). Wenn wir andererseits den Vektor mit einer Zahl kleiner als 1 multiplizieren, ist das Ergebnis ein Vektor kürzerer Länge (kleinerer Modul).
Hinweis: Verwechseln Sie das Produkt eines Vektors und eines Skalars nicht mit dem Skalarprodukt von Vektoren . Obwohl sie einen ähnlichen Namen haben, handelt es sich um zwei völlig unterschiedliche Konzepte.
Beispiel für das Produkt eines Vektors mit einem Skalar
Als nächstes sehen wir uns ein numerisches Beispiel an, wie das Produkt eines Vektors und einer Zahl berechnet wird:
- Multiplizieren Sie den folgenden Vektor mit 4:
![]()
![]()
Wie Sie gesehen haben, ist diese Art der Vektoroperation nicht sehr kompliziert, da Sie nicht viele Berechnungen durchführen müssen.
Es gibt jedoch kompliziertere Vektoroperationen wie Vektoraddition und Vektorsubtraktion. Wenn Sie bereits verstanden haben, wie man das Produkt eines Vektors und eines Skalars berechnet, empfehlen wir Ihnen, zur nächsten Ebene überzugehen und zu sehen, wie man Vektoraddition und Vektorsubtraktion löst, da es sich dabei um etwas schwierigere Operationen handelt und tatsächlich sie werden viel häufiger genutzt (sie sind wichtiger).
Eigenschaften der Multiplikation eines Vektors mit einer Zahl
Das Produkt eines Vektors und einer Zahl hat die folgenden Eigenschaften:
- Assoziative Eigenschaft : Wenn der Vektor mit mehr als einer Zahl multipliziert wird, spielt die Reihenfolge der Multiplikationen keine Rolle.
![]()
- Verteilungseigenschaft bezüglich der Addition und Subtraktion von Vektoren:
![]()
![]()
- Verteilungseigenschaft bezüglich der Addition von Skalaren:
![]()
- Neutrales Element : Offensichtlich ergibt jeder mit 1 multiplizierte Vektor den Vektor selbst:
![]()
Probleme der Multiplikation eines Vektors mit einem Skalar gelöst
Übung 1
Berechnen Sie analytisch das Ergebnis des Produkts des folgenden Vektors mit 3:
![]()
Um das Produkt zu finden, müssen Sie jede Koordinate des Vektors mit 3 multiplizieren:
![]()
Übung 2
Multiplizieren Sie den folgenden Vektor mit 6 und ermitteln Sie seinen Modul:
![]()
Wir multiplizieren zunächst den Vektor mit dem Skalar:
![]()
Es gibt nun zwei Möglichkeiten, den Betrag des erhaltenen Vektors zu berechnen. Die erste besteht darin, den Betrag des ursprünglichen Vektors zu ermitteln und ihn dann mit 6 zu multiplizieren:
![]()
![]()
Und die zweite Möglichkeit besteht darin, die Größe des bei der Multiplikation erhaltenen Vektors direkt zu berechnen:
![]()
Damit zeigt sich bei beiden Verfahren, dass das Ergebnis nicht von der Methode abhängt, mit der der Modul berechnet wird.
Übung 3
Aus dem folgenden Vektor:
![]()
Berechnen Sie die folgenden Operationen algebraisch:
![]()
![]()
![]()
![]()
Bestimmen Sie als Nächstes, ob die resultierenden Vektoren dieselbe Richtung und Richtung wie der ursprüngliche Vektor haben, und ordnen Sie sie vom kürzesten zum längsten.
Wir berechnen zunächst die Multiplikationen:
![]()
![]()
![]()
![]()
Daher haben Vektoren, die mit positiven Zahlen multipliziert werden, die gleiche Richtung und Richtung wie der ursprüngliche Vektor. Und mit negativen Zahlen multiplizierte Vektoren haben die gleiche Richtung, aber die entgegengesetzte Richtung zum ursprünglichen Vektor.
Vektoren gleicher Richtung und gleicher Richtung:
![]()
Und
![]()
Vektoren mit gleicher Richtung, aber unterschiedlicher Bedeutung:
![]()
Schließlich müssen wir die Vektoren nach ihrer Länge oder äquivalent ihrem Modul ordnen. Der Vektor mit der längsten Länge (oder dem größten Modul) ist derjenige, der mit einer größeren Zahl (im Absolutwert) multipliziert wurde, und der Vektor mit der kürzesten Länge (oder dem kleinsten Modul) ist derjenige, der mit einer kleineren Zahl multipliziert wurde Zahl (im absoluten Wert). Die Reihenfolge der Längen ist also:
![]()
Beachten Sie, dass die Länge oder der Modul nicht vom Vorzeichen des multiplizierten Skalars abhängt, da die Richtung des Vektors seinen Modul nicht ändert.
Übung 4
Betrachten Sie die folgenden zwei Vektoren:
![]()
Berechnen Sie die folgende Operation:
![]()
Wir lösen zunächst die Multiplikationen von Vektoren mit Zahlen:
![]()
![]()
![]()
Und dann subtrahieren wir die Vektoren:
![]()
![]()
Übung 5
Führen Sie die folgenden Multiplikationen von Vektoren mit Skalaren durch und stellen Sie die Ergebnisse grafisch dar:
![]()
![]()
![]()
![]()
![]()
Wir multiplizieren zunächst die Vektoren mit den reellen Skalaren:
![]()
![]()
![]()
![]()
![]()
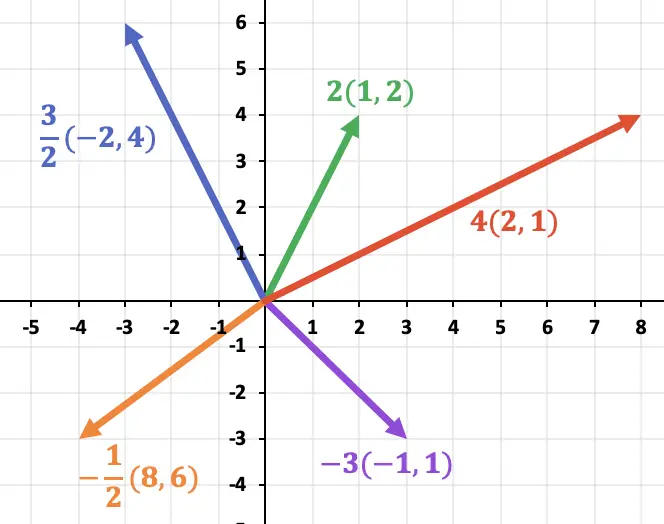
Nachdem wir schließlich die Vektoren berechnet haben, stellen wir sie im Diagramm dar: