Matrixkräfte

Auf dieser Seite werden wir sehen, wie man Potenzen von Matrizen berechnet. Außerdem finden Sie Beispiele und Schritt für Schritt gelöste Übungen zu Matrizenpotenzen, die Ihnen helfen, es perfekt zu verstehen. Außerdem erfahren Sie, was die n-te Potenz einer Matrix ist und wie Sie sie finden.

Wie wird die Potenz einer Matrix berechnet?

Um die Potenz einer Matrix zu berechnen, müssen Sie die Matrix so oft mit sich selbst multiplizieren, wie der Exponent angibt. Zum Beispiel:

A^4 = A \cdot A \cdot A \cdot A

Um die Potenz einer Matrix zu erhalten, müssen Sie daher wissen, wie man die Matrixmultiplikation löst. Andernfalls können Sie keine Potenzmatrix berechnen.

Beispiel für die Berechnung der Potenz einer Matrix:

Beispiele für Potenzen von 2x2-Matrizen

Daher wird die Potenz einer quadratischen Matrix berechnet, indem die Matrix mit sich selbst multipliziert wird. Ebenso ist eine kubische Matrix gleich der quadratischen Matrix der Matrix selbst. Um die Potenz einer auf vier erhöhter Matrix zu ermitteln, muss die auf drei erhöhte Matrix mit der Matrix selbst multipliziert werden. Und so weiter.

Es gibt eine wichtige Eigenschaft der Matrixleistung, die Sie kennen sollten: Die Leistung einer Matrix kann nur berechnet werden, wenn sie quadratisch ist , das heißt, wenn sie die gleiche Anzahl von Zeilen wie Spalten hat.

Was ist die Potenz n einer Matrix?

Die n-te Potenz einer Matrix ist ein Ausdruck, der es uns ermöglicht, jede Potenz einer Matrix einfach zu berechnen.

Oftmals folgen die Potenzen von Matrizen einem Muster . Wenn wir also die Reihenfolge, der sie folgen, entschlüsseln können, können wir jede Potenz berechnen, ohne alle Multiplikationen durchführen zu müssen.

Das bedeutet, dass wir eine Formel finden können, die uns die n-te Potenz einer Matrix liefert, ohne alle Potenzen berechnen zu müssen.

Tipps zum Entdecken des Musters, dem die Kräfte folgen:

  • Die Parität des Exponenten . Es kann sein, dass gerade Potenzen das eine und ungerade Potenzen das andere sind.
  • Variation von Zeichen. Beispielsweise könnte es sein, dass Elemente gerader Potenzen positiv und Elemente ungerader Potenzen negativ sind oder umgekehrt.
  • Wiederholung: ob dieselbe Matrix bei jeder bestimmten Anzahl von Potenzen wiederholt wird oder nicht.
  • Wir müssen auch prüfen, ob ein Zusammenhang zwischen dem Exponenten und den Elementen der Matrix besteht.

Beispiel für die Berechnung der Potenz n einer Matrix:

  • Sei

    A

    Berechnen Sie die folgende Matrix

    A^n

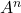
    Und

    A^{100}

    .

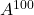
\displaystyle A = \begin{pmatrix} 1 & 1 \\[1.1ex] 1 & 1 \end{pmatrix}

Wir berechnen zunächst mehrere Potenzen der Matrix

A

, um zu versuchen, das Muster zu erraten, dem die Kräfte folgen. Also rechnen wir

A^2

,

A^3

,

A^4

Und

A^5:

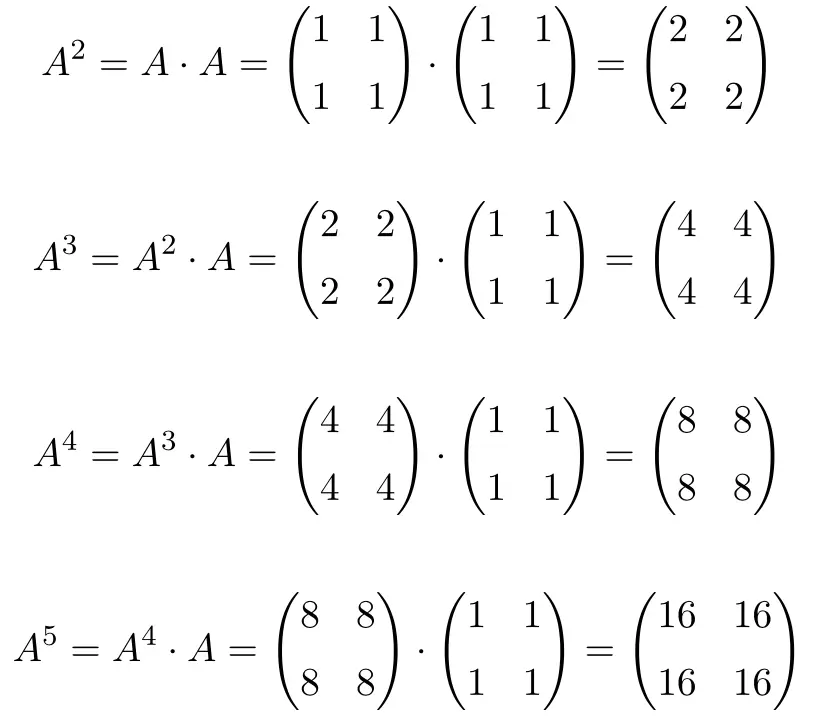
Schritt für Schritt gelöste Übung zu den Potenzen von 2x2-Matrizen

Bei der Berechnung bis

A^5

, sehen wir, dass die Potenzen der Matrix

A

Sie folgen einem Muster: Bei jeder Leistungssteigerung wird das Ergebnis mit 2 multipliziert. Daher sind alle Matrizen Potenzen von 2:

\displaystyle A^2= \begin{pmatrix} 2 & 2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 2^1 & 2^1 \\[1.1ex] 2^1 & 2^1 \end{pmatrix}

\displaystyle A^3= \begin{pmatrix} 4 & 4 \\[1.1ex] 4 & 4 \end{pmatrix}=\begin{pmatrix} 2^2 & 2^2 \\[1.1ex] 2^2 & 2^2 \end{pmatrix}

\displaystyle A^4= \begin{pmatrix} 8 & 8 \\[1.1ex] 8 & 8 \end{pmatrix}=\begin{pmatrix} 2^3 & 2^3 \\[1.1ex] 2^3 & 2^3 \end{pmatrix}

\displaystyle A^5= \begin{pmatrix} 16 & 16 \\[1.1ex] 16 & 16 \end{pmatrix}=\begin{pmatrix} 2^4 & 2^4 \\[1.1ex] 2^4 & 2^4 \end{pmatrix}

Wir können daher die Formel für die n-te Potenz der Matrix ableiten

A:

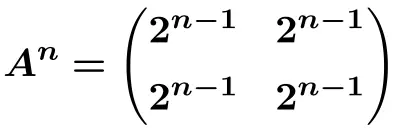
n-te Potenz einer 2x2-Matrix

Und aus dieser Formel können wir berechnen

A^{100}:

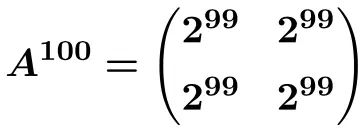
Übung Schritt für Schritt gelöst Potenz einer 2x2-Matrix

Probleme mit der Matrixleistung gelöst

Übung 1

Betrachten Sie die folgende Matrix der Dimension 2×2:

\displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix}

Berechnung:

\displaystyle A^4

Um die Potenz einer Matrix zu berechnen, müssen Sie die Matrix einzeln multiplizieren. Deshalb rechnen wir zunächst

\displaystyle A^2 :

\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1\end{pmatrix}

Jetzt rechnen wir

\displaystyle A^3 :

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} =\begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix}

Und schließlich rechnen wir

\displaystyle A^4 :

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} \bm{-7} & \bm{-8} \\[1.1ex] \bm{4} & \bm{-7} \end{pmatrix}

Übung 2

Betrachten Sie die folgende Matrix der Ordnung 2:

\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}

Berechnung:

\displaystyle A^{35}

\displaystyle A^{35}

ist eine zu große Potenz, um sie manuell zu berechnen, daher müssen die Matrixpotenzen einem Muster folgen. Also lasst uns rechnen

\displaystyle A^5

um zu versuchen, die Reihenfolge zu verstehen, der sie folgen:

\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}

Auf diese Weise können wir das Muster erkennen, dem die Potenzen folgen: Bei jeder Potenz bleiben alle Zahlen gleich, mit Ausnahme des Elements in der zweiten Spalte der zweiten Zeile, das mit 3 multipliziert wird. Daher bleiben alle Zahlen immer gleich. und das letzte Element ist eine Potenz von 3:

\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^1 \end{pmatrix}

\displaystyle A^2=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^2 \end{pmatrix}

\displaystyle A^3=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^3 \end{pmatrix}

\displaystyle A^4=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^4 \end{pmatrix}

\displaystyle A^5=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^5 \end{pmatrix}

Also die Formel für die n-te Potenz der Matrix

\displaystyle A

Ost:

\displaystyle A^n=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^n\end{pmatrix}

Und aus dieser Formel können wir berechnen

\displaystyle A^{35}:

\displaystyle\bm{A^{35}=}\begin{pmatrix} \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{3^{35}}\end{pmatrix}

Übung 3

Betrachten Sie die folgende 3×3-Matrix:

\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Berechnung:

\displaystyle A^{100}

\displaystyle A^{100}

ist eine zu große Potenz, um sie manuell zu berechnen, daher müssen die Matrixpotenzen einem Muster folgen. Also lasst uns rechnen

\displaystyle A^5

um zu versuchen, die Reihenfolge zu verstehen, der sie folgen:

\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Auf diese Weise können wir das Muster erkennen, dem die Potenzen folgen: Bei jeder Potenz bleiben alle Zahlen gleich, mit Ausnahme von Brüchen, die im Zähler um eins wachsen:

\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^2= \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^3= \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^4= \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^5= \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Also die Formel für die Potenz der n-ten Matrix

\displaystyle A

Ost:

\displaystyle A^n= \begin{pmatrix} 1 & \frac{n}{5} & \frac{n}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Und aus dieser Formel können wir berechnen

\displaystyle A^{100}:

\displaystyle A^{100}= \begin{pmatrix} 1 & \frac{100}{5} & \frac{100}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} \bm{1} & \bm{20} & \bm{20} \\[1.1ex] \bm{0} & \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{1} \end{pmatrix}

Übung 4

Betrachten Sie die folgende Matrix der Größe 2×2:

\displaystyle A=\begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}

Berechnung:

\displaystyle A^{201}

\displaystyle A^{201}

ist eine zu große Potenz, um sie manuell zu berechnen, daher müssen die Matrixpotenzen einem Muster folgen. In diesem Fall ist eine Berechnung erforderlich

\displaystyle A^{8}

Um die Reihenfolge zu kennen, folgen sie:

\displaystyle A^2= A \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}

\displaystyle A^6= A^5 \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}

\displaystyle A^7= A^6 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}

\displaystyle A^8= A^7 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}

Mit diesen Berechnungen können wir sehen, dass wir alle 4 Potenzen die Identitätsmatrix erhalten. Das heißt, dass es uns als Ergebnis die Identitätsmatrix der Mächte liefert

\displaystyle A^4

,

\displaystyle A^8

,

\displaystyle A^{12}

,

\displaystyle A^{16}

,… Also zum Berechnen

\displaystyle A^{201}

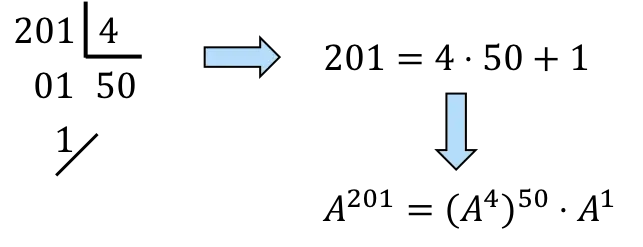
wir müssen 201 in Vielfache von 4 zerlegen:

Schritt für Schritt gelöste Übung zu den Potenzen von 2x2-Matrizen und der Potenz n

\displaystyle 201= 4 \cdot 50 +1

,Noch,

A^{201}

es wird 50 Mal sein

\displaystyle A^{4}

und einmal

\displaystyle A^{1}:

\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1

Und woher wissen wir das?

\displaystyle A^4

ist die Identitätsmatrix

\displaystyle I :

\displaystyle A^4 =I

\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1 = I^{50}\cdot A

Darüber hinaus ergibt die auf eine beliebige Zahl erhöhte Identitätsmatrix die Identitätsmatrix. Noch:

\displaystyle A^{201}= I^{50}\cdot A = I \cdot A

Und schließlich ergibt jede mit der Identitätsmatrix multiplizierte Matrix dieselbe Matrix. ALSO:

\displaystyle A^{201}= I \cdot A = A

Wofür

A^{201}

ist gleich

A:

\displaystyle A^{201}= A =\begin{pmatrix} \bm{0} & \bm{-1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}

Übung 5

Betrachten Sie die folgende Matrix der Ordnung 3:

\displaystyle A=\begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}

Berechnung:

\displaystyle A^{62}

Berechnen Sie natürlich die Potenz der Matrix

\displaystyle A^{62}

Dies ist eine zu umfangreiche Berechnung, um sie manuell durchzuführen, daher müssen die Matrixpotenzen einem Muster folgen. In diesem Fall ist eine Berechnung erforderlich

\displaystyle A^{6}

Um die Reihenfolge zu kennen, folgen sie:

\displaystyle A^2= A \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}

\displaystyle A^6= A^5 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Mit diesen Berechnungen können wir sehen, dass wir alle 3 Potenzen die Identitätsmatrix erhalten. Das heißt, dass es uns als Ergebnis die Identitätsmatrix der Mächte liefert

\displaystyle A^3

,

\displaystyle A^6

,

\displaystyle A^{9}

,

\displaystyle A^{12}

,… Also das zu berechnen

\displaystyle A^{62}

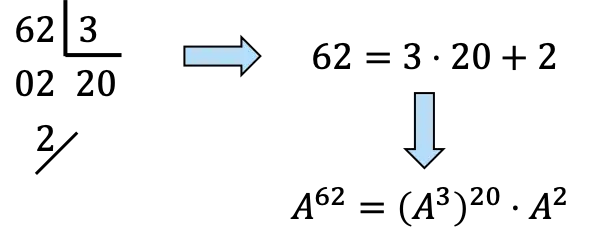
Wir müssen 62 in Vielfache von 3 zerlegen:

Übung Schritt für Schritt einer Potenz einer 3x3-Matrix gelöst, n-te Potenz

\displaystyle 62= 3 \cdot 20 +2

,Noch,

\displaystyle A^{62}

es wird 20 Mal sein

\displaystyle A^{3}

und einmal

\displaystyle A^{2}:

\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2

Und woher wissen wir das?

\displaystyle A^3

ist die Identitätsmatrix

\displaystyle I :

\displaystyle A^3 =I

\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2 = I^{20}\cdot A^2

Darüber hinaus ergibt die auf eine beliebige Zahl erhöhte Identitätsmatrix die Identitätsmatrix. Noch:

\displaystyle A^{62}= I^{20}\cdot A^2 = I \cdot A^2

Schließlich ergibt jede mit der Identitätsmatrix multiplizierte Matrix dieselbe Matrix. Noch:

\displaystyle A^{62}= I \cdot A^2 = A^2

Wofür

A^{62}

wird gleich sein

A^{2}

, für den wir zuvor das Ergebnis berechnet haben:

\displaystyle A^{62}= A^2=\begin{pmatrix} \bm{3} & \bm{3} & \bm{1} \\[1.1ex] \bm{-2} & \bm{-2} & \bm{-1} \\[1.1ex] \bm{0} & \bm{1} & \bm{-1} \end{pmatrix}

Wenn diese Übungen zu den Potenzen quadratischer Matrizen für Sie hilfreich waren, finden Sie hier auch gelöste Schritt-für-Schritt-Übungen zur Addition und Subtraktion von Matrizen , einer der am häufigsten verwendeten Operationen mit Matrizen.

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen