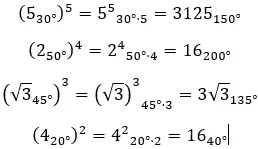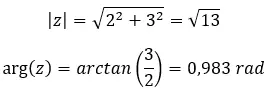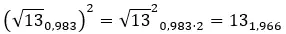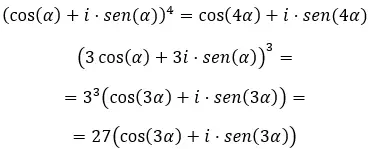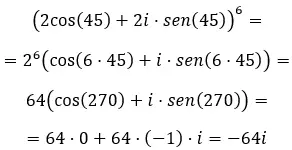Das Lösen der Potenzen komplexer Zahlen ist ziemlich einfach, wenn man die richtige Methode kennt. Daher erklären wir in diesem Artikel, wie man komplexe Potenzen auf drei Arten löst: für komplexe Zahlen in Binomialform, in Polarform und in trigonometrischer Form.
Wie löst man die Potenz einer komplexen Zahl?
Wie bereits in der Einleitung erwähnt, können beim Umgang mit komplexen Befugnissen drei Situationen auftreten. Die erste und einfachste Möglichkeit besteht darin, dass wir die Zahl in Polarform erhalten. Im zweiten Fall erhalten wir die Zahl in Binomialform und im dritten Fall erhalten wir die Zahl in trigonometrischer Form.
Mit anderen Worten: Beim Arbeiten mit Komplexen in polarer Form lässt sich die Aufgabe schneller lösen. Daher empfiehlt es sich, die jeweilige Zahl in die Polarform umzuwandeln. Aber eigentlich sind alle Methoden einfach zu lösen . Wir erklären Ihnen jedoch, wie alle Fälle gelöst werden, und bieten Ihnen eine Übung an.
Potenzen komplexer Zahlen in Polarform
Wenn wir komplexe Potenzen in Polarform lösen wollen, erhöhen wir einfach den Modul auf beliebig und multiplizieren das Argument mit n. Mathematisch ausgedrückt erhalten wir folgende Formel:
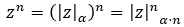
Hier sind einige Beispiele, damit Sie versuchen können, sie selbst zu lösen:
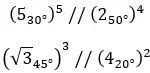
Potenzen komplexer Zahlen in Binomialform
Wenn wir andererseits komplexe Potenzen in Binomialform lösen wollen, können wir zwei verschiedene Methoden verwenden. Der erste befasst sich mit der Lösung der Potenz auf „algebraische“ Weise (die Auflösung erfolgt so, als ob ich eine Variable wäre). Und das zweite System besteht darin, die Binomialform in eine Polarform umzuwandeln und dann dem vorherigen Verfahren zu folgen.
Wenn Sie nicht wissen, wie Sie von der Binomialform zur Polarform gelangen, erklären wir Ihnen das ganz anschaulich in unserem Artikel über komplexe Zahlen . Aber jetzt werden wir es schnell anhand eines Beispiels sehen.
Versuchen Sie, die folgende komplexe Potenz zu lösen: (2 + 3i) 2 .
Potenzen komplexer Zahlen in trigonometrischer Form
Wenn wir schließlich komplexe Potenzen in trigonometrischer Form lösen wollen, müssen wir die bekannte Formel von de Moivre verwenden. Was wie folgt geschrieben ist:
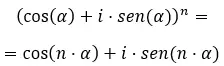
Wenn Sie diese Formel kennen, versuchen Sie, die folgenden Übungen zu lösen:

Erfahren Sie mehr über komplexe Kräfte
- Komplexe Zahlen
- Eigenschaften von Komplexen
- Operationen mit komplexen Zahlen
- komplexe Wurzeln