Polynom

Ein Monom ist ein algebraischer Ausdruck , der durch einen Koeffizienten (numerischen Wert) gebildet wird, der eine Variable mit einem Exponenten multipliziert. Beispielsweise ist der Ausdruck 4x² ein Monom. Aus diesem mathematischen Konzept gelangen wir zum Polynom, einem Satz von Additionen und Subtraktionen mehrerer Monome. Im Bild oben sehen Sie ein Beispiel für die Struktur eines Polynoms, das aus mehreren Monomen besteht.

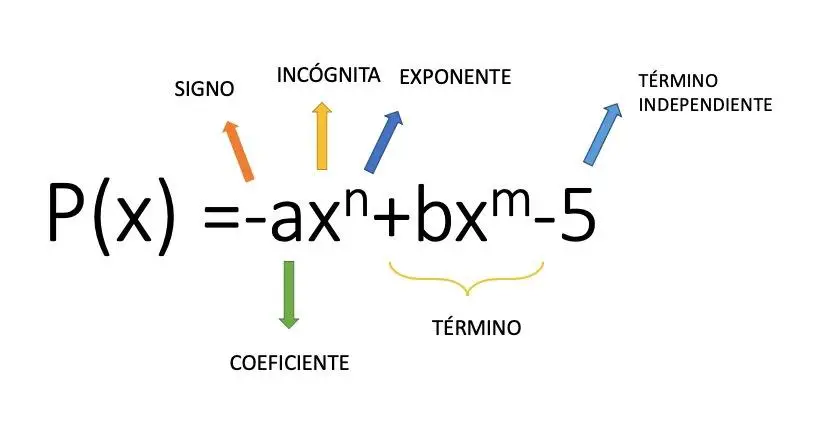
Arten von Polynomen

Durch den Exponenten eines bestimmten Monoms können wir Polynome in verschiedene Typen einteilen. Wir können diese Ausdrücke in Kategorien einteilen wie: Polynom ersten Grades, Polynom zweiten Grades, Polynom dritten Grades usw. Grundsätzlich müssen Sie das Monom identifizieren, das den größten Exponenten hat und den Grad des Polynoms darstellt. Und sobald Sie es wissen, können Sie es einem der Typen zuordnen, über die wir gerade gesprochen haben.

Polynom mehrerer Variablen

Darüber hinaus gibt es noch eine andere Möglichkeit, Polynome zu organisieren, nämlich nach der Anzahl der Monome, aus denen sie bestehen. Wenn wir beispielsweise ein Binomial haben, entspricht dies einem Polynom mit zwei Termen. Wenn wir ein Trinom haben, entspricht dies einem Polynom mit drei Termen usw. Alle diese Arten der Katalogisierung von Polynomen haben unendlich viele Unterkategorien. Denn diese Ausdrücke können aus beliebigen Monomen zusammengesetzt sein und auch beliebige Grade haben.

Eigenschaften und Eigenschaften von Polynomen

• Absoluter Grad eines Polynoms: Im vorherigen Abschnitt haben wir die Definition des relativen Grades besprochen. Bei Polynomen, die aus mehr als einer Variablen bestehen, haben wir jedoch den absoluten Grad, der der maximalen Summe der Exponenten aller Variablen dieses Monoms entspricht. Beispielsweise ist im Monom 5x²y³ der absolute Grad gleich 2 + 3 = 5.
• Geordnetes Polynom: Wir definieren ein geordnetes Polynom in Bezug auf eine Variable, wenn die Exponenten dieser Variablen in aufsteigender oder absteigender Reihenfolge angeordnet sind. Wenn wir beispielsweise dieses Polynom P(x) = 3x + 4x³ – x² finden, wird es in diesem Fall nicht geordnet sein. Also sollten wir es korrigieren und wir würden dieses Ergebnis erhalten: P(x) = 4x³ – x² + 3x.
• Vollständiges Polynom: Wenn wir ein Polynom finden, das Monome mit allen möglichen Exponenten hat (vom höchsten Grad bis zum unabhängigen Term), sagen wir, dass es ein vollständiges Polynom ist. Beispielsweise ist der folgende Ausdruck: P(x) = 3 x² + 2x – 4 von diesem Typ, da zwischen 2 und 0 kein Exponent fehlt.
• Homogenes Polynom: ist das Polynom, das in jedem seiner Monome den gleichen absoluten Grad hat. Variablen können im Exponenten unterschiedliche Werte haben, die Summe der Exponenten der Variablen in allen Monomen muss jedoch unbedingt gleich sein. Zum Beispiel: P(x) = x²y³z + 3 x ⁴ yz, die beiden Summen ergeben sechs 2 + 3 + 1 = 4 + 1 + 1 = 6.
• Identische Polynome: Wenn wir zwei oder mehr Polynome finden, die die Koeffizienten derselben Terme teilen, dann werden wir sagen, dass es sich um identische Polynome handelt. Unten sehen Sie ein Beispiel zwischen zwei Polynomen: P(x) = 2x + 27 und Q(x) = 5 (x + 3) – 3 (x – 4). Sie sind identisch, da sie die Koeffizienten jedes Exponenten gemeinsam haben : 2x = 5x – 3x und 27 = 15 + 12.
• Nullpolynom: Dieses Polynom hat nur Nullkoeffizienten (gleich Null), daher ist der Gesamtwert des Polynoms ebenfalls Null. Das Polynom P(x) = 0x³ + 0x² – 0x – 0 ist ein klares Beispiel für diese Art von Polynom, es sollte jedoch nicht mit Q(x) = 0 verwechselt werden, da Sie in diesem Fall eine Gleichung bilden und dies nicht der Fall ist bedeutet nicht, dass alle Koeffizienten von Q(x) 0 sind.

Numerischer Wert eines Polynoms

Der numerische Wert eines Polynoms ist das Ergebnis, das wir erhalten, wenn wir die Variable dieses Ausdrucks durch eine Zahl ersetzen. Wir müssen dieses Polynom einfach so lösen, als wäre es eine kombinierte Operation . Als Nächstes erklären wir die drei Methoden, mit denen Sie den numerischen Wert eines solchen Ausdrucks ermitteln können.

• Direkter Ersatz: Wenn wir direkt die Werte erhalten, die jeder Variablen des Polynoms entsprechen, ersetzen wir diese Zahlen einfach durch diese Variablen. Wenn wir also das Polynom P(x) = 2x² – x + 4 haben und uns gesagt wird, dass x = 3, dann ist der numerische Wert des Polynoms gleich 2 · 3² – 3 + 4 = 19.
• Variablenauflösung: Wir werden diesen Fall anwenden, wenn sie uns nicht direkt den Wert der Variablen, sondern eine Äquivalenz liefern. Wenn zum Beispiel P(2) P(x – 1) = x³ – 2x + 1 wahr ist, dann lösen wir zuerst die Gleichung 2 = x – 1 und erhalten x = 3. Schließlich müssen wir 3 durch ersetzen x, so dass 3³ – 2 · 3 + 1 = 22.
• Änderung der Variablen: wenn wir ein Polynom P(x) = 4x – 2 haben und diesen Wert für P(x + 2) wissen wollen. Als nächstes müssen wir alle x im Ausdruck in a(x+2) ändern. Schauen wir uns jedoch an, wie dieses letzte gelöste Beispiel aussehen würde: P (x + 2) = 4 (x + 2) – 2.

Operationen mit Polynomen

Im Folgenden erklären wir, wie man die vier Grundrechenarten mit Polynomen löst, immer der Hierarchie der Operationen folgend. In jedem Abschnitt finden Sie eine kleine Theorie, die Ihnen zeigt, wie Sie im jeweiligen Fall vorgehen müssen, sowie einige praktische Beispiele.

Addition von Polynomen

Um Polynome hinzuzufügen, müssen wir die Tatsache berücksichtigen, dass sie nur nach ähnlichen Termen gruppiert werden können, wenn wir also die Polynome P(x) = 3x³ – x² + 2x – 4 und Q(x) = 2x² + 3x – 2 haben. Um also P(x) + Q(x) zu erhalten, addieren wir die Koeffizienten der beiden Polynome zusammen mit demselben Exponenten: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. Zusammenfassend können wir sagen, dass wir die Koeffizienten jedes ähnlichen Termes gruppiert und addiert haben und am Ende alle Terme in einem einzigen Polynom ausgedrückt haben .

Subtraktion von Polynomen

Die Subtraktion von Polynomen wird auf die gleiche Weise gelöst wie die Addition, der einzige Unterschied ist offensichtlich das Symbol. Dann gruppieren wir ähnliche Begriffe, subtrahieren sie und wandeln alles in einen einzigen Ausdruck um. Nachfolgend zeigen wir Ihnen anhand eines Beispiels: P(x) = 5x³ – 2x² + x – 3 und Q(x) = 3x² + 5x + 4, dann P(x) – Q(x) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.

Polynommultiplikation

Bei der Lösung dieser Art von Multiplikation kann es etwas kompliziert werden, aber wenn Sie alle Schritte befolgen, die wir Ihnen erklären, ist alles in Ordnung. Bei dieser mathematischen Operation werden alle Monome mit allen anderen operieren, das heißt, wir werden nicht nur ähnliche Terme multiplizieren. Darüber hinaus ändern sich nicht nur die Koeffizienten , sondern auch die Exponenten . Anhand dieses Beispiels werden Sie alles viel besser verstehen: P(x) = 2x² + 3x – 1 und Q(x) = 2x + 3:

P(x) Q(x) = ( 2x² + 3x –1 ) · ( 2x + 3 ) = 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3

Im Grunde multiplizieren wir die Koeffizienten jedes Termes eines Polynoms mit denen des zweiten und wenden dann die Potenzeigenschaft a ⁿ · a ^m = a ^n+m an.

Division von Polynomen

Abschließend müssen wir nur noch erklären, wie man die Division von Polynomen löst. Im Grunde müssen wir die Verteilungseigenschaft der Division anwenden: (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷ d). Und wir werden auch die folgende Potenzierungseigenschaft auf ⁿ ÷ a ^m = a ^nm anwenden. Wir werden dies nun anhand eines einfachen Beispiels sehen: P(x) = 3x³ – 6x² + 9x und Q(x) = 3x.

P(x) ÷ Q(x) = ( 3x³ – 6x² +9x ) ÷ 3x = ( 3x³ ÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = x² – 2x + 3

Nachdem Sie nun gesehen haben, wie Sie alle diese Operationen mit Polynomen lösen können, hoffen wir, dass Sie wissen, wie Sie es in der Praxis anwenden können. Wenn Sie jedoch der Meinung sind, dass dies nicht der Fall ist und Sie noch ein wenig üben möchten, empfehlen wir Ihnen, sich einige gelöste Übungen auf dieser Seite anzusehen. Diese werden Ihnen dabei helfen, all diese mathematischen Konzepte vollständig zu verinnerlichen.

Faktorisierung von Polynomen

Um Polynome zu faktorisieren, können Sie dies manuell tun, wie im Artikel in diesem letzten Link beschrieben, oder Sie können es mit einem Ruffini-Rechner tun. Wir empfehlen, diese zweite Option zu verwenden, wenn Sie es schnell erledigen möchten. Wenn Sie jedoch nur das Faktorisieren lernen, ist es besser, manuell zu üben. Die Art und Weise, dies zu tun, sollte basierend auf Ihrer Situation gewählt werden.

Lösen Sie Polynome mit dem wissenschaftlichen Taschenrechner

Heutzutage gibt es viele verschiedene wissenschaftliche Taschenrechner auf dem Markt. Wenn Sie jedoch auf der Suche nach einem günstigen Taschenrechner sind , der Polynome lösen kann , empfehlen wir Ihnen den Casio FX-991SPX II . Es ist einfach zu bedienen, sehr leistungsstark und funktional und eignet sich daher perfekt für jeden Mathematikschüler der Mittel- und Oberstufe. Im Folgenden erklären wir kurz, wie mathematische Ausdrücke dieses Stils mit diesem oder einem ähnlichen Casio-Modell gelöst werden.

Sie müssen zuerst den numerischen Wert der Variablen eingeben, ihn schreiben und dann „STO“ + Buchstaben der Variablen drücken, zum Beispiel x. Wenn also alle Variablen definiert sind, müssen Sie nur noch den Polynomausdruck so schreiben, wie er für alle Variablen und alle Zahlen gilt. Und schließlich müssen Sie die Gleichheitstaste drücken, um das Ergebnis zu erhalten, das dem numerischen Wert des Polynoms entspricht.