Die Zahl Pi ist eine mathematische Konstante , die das Verhältnis zwischen dem Umfang eines Kreises und seinem Durchmesser darstellt. Es ist eine irrationale Zahl. Mit anderen Worten, es handelt sich nicht um einen exakten Bruch . Daher kann sie nicht als endliche Dezimalzahl dargestellt werden. Der Wert von Pi beträgt ungefähr 3,14159 und wird durch den griechischen Buchstaben π dargestellt.
Pi ist eine wichtige Zahl in der Mathematik. Daher gibt es viele Anwendungen in verschiedenen Bereichen. Beispielsweise wird es in der Geometrie zur Flächenberechnung verwendet. Auch der Umfang von Kreisen und anderen kreisförmigen Figuren. Andererseits in der Trigonometrie zur Berechnung von Winkeln und Längen von Bögen. Schließlich dient es in den Ingenieurwissenschaften und der Physik der Berechnung von Größen wie Volumen und Kapazität.
Der Pi-Tag wird jedes Jahr am 14. März gefeiert, da das Datum nahe am Wert von Pi (3,14) liegt. Dieses Datum wird gefeiert, um Pis Rolle in der Mathematik zu würdigen und das Interesse an dieser Grundkonstante zu fördern.
Wer hat die Zahl Pi entdeckt?
Die Zahl Pi ist seit der Antike bekannt und wurde vom griechischen Mathematiker Archimedes (287-212 v. Chr.) genau beschrieben . Tatsächlich berechnete er damit die Fläche und das Volumen geometrischer Figuren.
Im 18. Jahrhundert bewies der Schweizer Mathematiker Johann Lambert, dass Pi eine irrationale Zahl ist. Später, im 19. Jahrhundert, erklärte der deutsche Mathematiker Ferdinand von Lindemann, dass Pi eine transzendente Zahl sei. Das heißt, es kann nicht als exakte Lösung einer Polynomgleichung mit rationalen Koeffizienten ausgedrückt werden.
Im Laufe der Geschichte haben verschiedene Mathematiker zum Verständnis der Zahl Pi beigetragen und Techniken entwickelt, um sie genauer zu berechnen. Auch heute noch ist Pi eine der wichtigsten und bekanntesten mathematischen Konstanten der Welt und wird in der Mathematik weiterhin untersucht.
Warum ist die Zahl Pi unendlich?
Der Wert von Pi beträgt ungefähr 3,14159, aber in Wirklichkeit handelt es sich um eine Zahl, die nach dem Dezimalpunkt auf unbestimmte Zeit weiterläuft . Das bedeutet, dass Pi eine unendliche Zahl ist und nicht vollständig durch eine Dezimalzahl dargestellt werden kann.
Obwohl der Wert von Pi unendlich ist, können in der Praxis Näherungswerte von Pi mit großer Präzision berechnet werden. Mittlerweile wurden Millionen Stellen von Pi berechnet und es hat sich gezeigt, dass die Dezimalstellen keine regelmäßigen Muster aufweisen. Allerdings geschah dies über Supercomputer, da wir nicht so viele Zahlen berechnen können.
Welche Methoden gibt es, um den Näherungswert der Zahl Pi zu berechnen?
Es gibt mehrere praktische Methoden, um den Wert von Pi zu berechnen. Als nächstes erklären wir Schritt für Schritt die drei von Mathematikern am häufigsten verwendeten Methoden.
1. Methode von Archimedes
Der griechische Mathematiker Archimedes verwendete eine geometrische Methode, um einen Näherungswert von Pi zu berechnen. Um diese Methode zu verwenden, führen Sie die folgenden Schritte aus:
1. Zeichnen Sie einen Kreis und ziehen Sie eine Linie durch den Mittelpunkt des Kreises und schneiden Sie diese an zwei gegenüberliegenden Punkten, wie unten gezeigt:
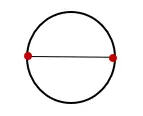
2. Messen Sie die Länge der Linie, die den Kreis schneidet, und beschriften Sie sie mit „D“. Dieses Maß ist der Durchmesser des Kreises.
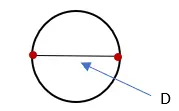
3. Messen Sie die Länge der Linie, die den Kreis bildet, und beschriften Sie sie mit „C“. Dieses Maß ist der Umfang des Kreises.
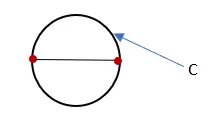
4. Teilen Sie den Umfang des Kreises (C) durch den Durchmesser des Kreises (D). Das Ergebnis ist ein Näherungswert von Pi.
Beispiel: Wenn der Durchmesser des Kreises 6 und der Umfang 18 beträgt, dann ist der ungefähre Wert von Pi 18 ÷ 6 = 3. Natürlich ist dieses Beispiel sehr einfach, aber wenn man es mit Werten eines tatsächlichen Umfangs macht , werden Sie sehen, dass die Methode korrekt funktioniert.
Wir empfehlen sogar, es auszuprobieren: Messen Sie eine Tasse oder etwas, das eine runde Form hat, und prüfen Sie, ob es für Sie funktioniert.
2. Monte-Carlo-Methode
Die Monte-Carlo-Methode ist eine probabilistische Methode zur Berechnung von Näherungswerten von Pi. Dazu wird eine große Anzahl von Punkten zufällig auf einer Ebene generiert und die Anzahl der Punkte gezählt, die in einen in ein Quadrat eingeschriebenen Kreis passen. Der Prozess wird wie folgt angewendet:
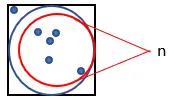
1. Zeichnen Sie einen Kreis in ein Quadrat mit Seite 1, wie unten gezeigt:

2. Generieren Sie zufällig eine große Anzahl von Punkten im Quadrat.
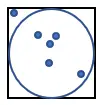
3. Zählen Sie die Anzahl der Punkte, die in den Kreis passen. Nennen wir diese Größe „n“.
4. Zählen Sie die Gesamtzahl der generierten Punkte. Nennen Sie diese Größe „m“.
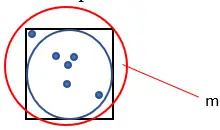
5. Berechnen Sie den ungefähren Wert von Pi mithilfe der folgenden Formel: Pi = (4 · n) ÷ m.
Wenn beispielsweise 380 Punkte generiert wurden und 300 in den Kreis passen, beträgt der ungefähre Wert von Pi (4 · 300) ÷ 380 = 3,16. Dieser Wert ähnelt stark den ersten beiden Dezimalstellen von Pi, aber genau wie bei der vorherigen Methode erhalten Sie durch die Verwendung tatsächlicher Messungen einen noch genaueren Wert .
3. Iterationsmethode
Die Iterationsmethode ist eine mathematische Methode zur Berechnung von Näherungswerten von Pi. Diese Methode verwendet eine Formel, die den Wert von Pi impliziert und iterativ angewendet wird, um die Genauigkeit der Berechnung zu verbessern. Hier sind die Schritte zur Verwendung dieser Methode:
- Wählen Sie einen Anfangswert für Pi. Beispielsweise können Sie den Wert 3 wählen.
- Verwenden Sie eine Formel, die den Wert von Pi berücksichtigt, um einen neuen Näherungswert zu berechnen. Sie können beispielsweise die folgende Formel verwenden: Pi = (Pi + (4 ÷ Pi)) ÷ 2
- Vergleichen Sie den neuen Näherungswert mit dem alten Wert. Wenn der Unterschied zwischen beiden gering genug ist, haben Sie ein genaues Ergebnis erhalten. Wenn der Unterschied immer noch signifikant ist, weisen Sie Pi den neuen Wert zu und wiederholen Sie den Vorgang ab Schritt 2.
Wenn der Anfangswert von Pi beispielsweise 3 ist, wäre der neue Näherungswert (3 + (4 ÷ 3)) ÷ 2 = 2,66666666. Da der Unterschied zwischen beiden jedoch nicht sehr gering ist , können Sie den Vorgang jederzeit mehrmals wiederholen, bevor Sie einen genauen Wert ermitteln.
Welche Anwendungen gibt es für die Zahl Pi?
Pi ist eine wichtige Zahl in der Mathematik und hat viele Anwendungen in verschiedenen Bereichen. Zu den wichtigsten Anwendungen von Pi gehören:
Geometrie
Pi wird in der Geometrie verwendet, um die Fläche und den Umfang von Kreisen und anderen kreisförmigen Figuren zu berechnen:
- Kreise : Berechnen Sie die Fläche und den Umfang der Kreise.
- Kugeln : Bestimmen Sie die Fläche und das Volumen der Kugeln.
- Zylinder : Berechnung der Oberfläche und des Volumens von Zylindern.
- Kegel – Wird zur Berechnung der Oberfläche und des Volumens von Kegeln verwendet.
Trigonometrie
Es ist in der Trigonometrie nützlich zur Berechnung von Winkeln und Bogenlängen. Einige seiner Anwendungen sind:
- Winkel : Berechnung von Winkeln und Bogenlängen.
- Trigonometrische Funktionen – werden zur Berechnung des Werts trigonometrischer Funktionen für bestimmte Winkel verwendet.
- Zirkuläre Trigonometrie : Zur Berechnung der Werte trigonometrischer Funktionen für Winkel von 360 Grad.
Maschinenbau
Im Ingenieurwesen wird Pi zur Berechnung von Größen wie Volumen und Kapazität verwendet. Einige seiner Anwendungen sind:
- Elektronik : Berechnen Sie Größen wie Widerstand und Kapazität.
- Elektrizität : Sie wird zur Berechnung von Größen wie Leistung und elektrischer Energie verwendet.
- Bauingenieurwesen : Berechnen Sie Größen wie die Oberfläche und das Volumen von Bauwerken und Bauelementen.
Körperlich
Die Zahl Pi (π) ist eine mathematische Konstante, die in der Physik viele Anwendungen hat. Hier sind einige Beispiele für die Verwendung von Pi in der Physik:
- Wellen – Wird zur Berechnung der Frequenz und Wellenlänge von Wellen verwendet.
- Mechanik : In der Mechanik ist es nützlich zur Berechnung von Arbeit und Energie in rotierenden Systemen.
- Elektromagnetismus : Im Elektromagnetismus kann damit die in einem Kondensator gespeicherte Energie und die Induktivität in einer Wicklung berechnet werden.
- Kosmologie In der Kosmologie wird Pi zur Berechnung der Krümmung der Raumzeit und der Ausdehnung des Universums verwendet.
Welche Anwendungen hat die Zahl Pi im wirklichen Leben?
Hier sind einige Beispiele, wie Pi im Alltag verwendet wird:
- Geometrie : um die Fläche einer kreisförmigen Matte zu definieren oder um die Länge eines Maßbandes zu messen, das benötigt wird, um den Umfang eines runden Tisches abzudecken.
- Kochen – Bestimmen, wie viel Wasser oder Flüssigkeit benötigt wird, um einen Topf zu füllen, oder wie viele Zutaten in einen runden Behälter passen.
- Astronomie : Kennen Sie die Entfernung zwischen den Planeten und den Sternen, die Umlaufbahn der Planeten und die Position der Himmelskörper am Himmel.
- Gartenarbeit : Ermitteln Sie die Menge an Erde oder Erde, die zum Füllen eines runden Topfes benötigt wird, oder berechnen Sie die Wassermenge, die zum Gießen einer Pflanze in einem runden Garten benötigt wird.