In diesem Artikel erklären wir, was die Periodizität einer Funktion ist. Darüber hinaus sehen Sie einige Beispiele für periodische Funktionen. Abschließend analysieren wir die Periode trigonometrischer Funktionen, da sie eines ihrer wichtigsten Merkmale ist.
Was ist die Periodizität einer Funktion?
Die Periodizität einer Funktion ist ein Merkmal von Funktionen, die ihre Werte zyklisch wiederholen, d. h. eine Funktion ist periodisch, wenn sich ihr Graph in jedem bestimmten Intervall wiederholt. Dieses Intervall wird als Periode bezeichnet.
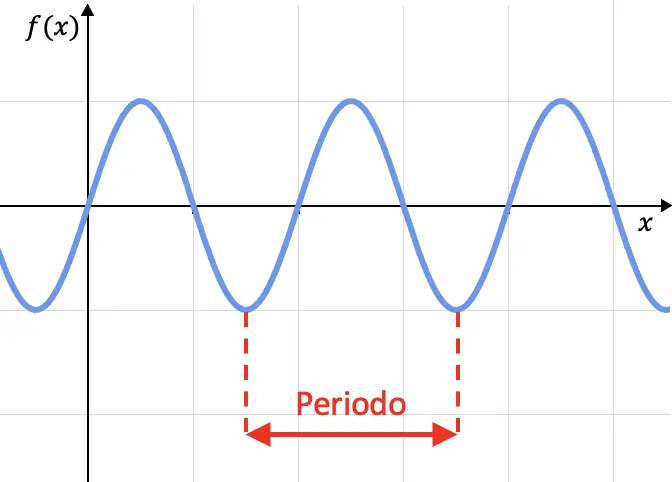
Mathematisch ist eine Funktion nur dann periodisch, wenn sie erfüllt ist
![]()
für jeden Wert der unabhängigen Variablen x.
![]()
Wobei T die Periode der periodischen Funktion i k ganzzahlig ist.
Beispiele für Funktionsperiodizitäten
Sobald wir das Konzept der Periodizität einer Funktion kennengelernt haben, werden wir mehrere Beispiele für die Berechnung der Periodizität einer Funktion sehen.
Beispiel 1
Bestimmen Sie, ob die folgende Funktion periodisch ist:
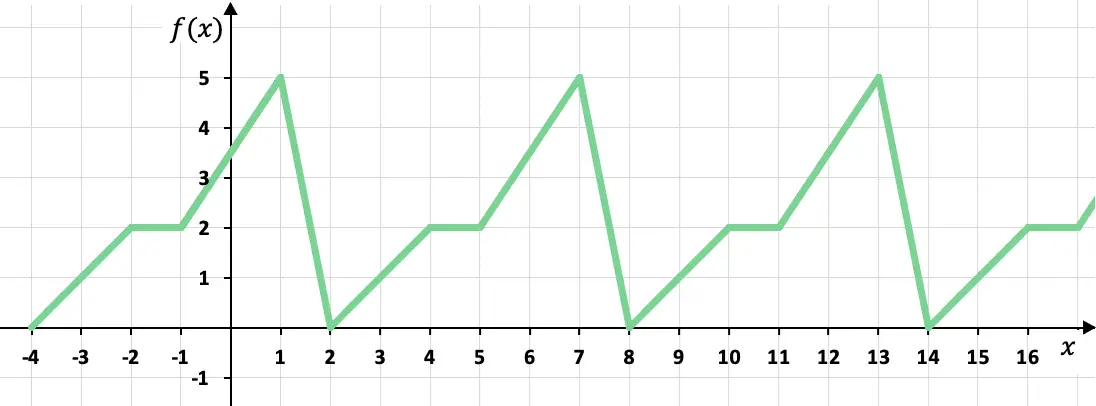
Diese stückweise definierte Funktion ist eine periodische Funktion, da sich die Werte ihres Graphen zyklisch wiederholen. Genauer gesagt nimmt die Funktion alle sechs x den gleichen Wert an, daher ist die Periode der Funktion gleich 6.
![]()
Beispiel 2
Finden Sie die Periodizität der folgenden Funktion:
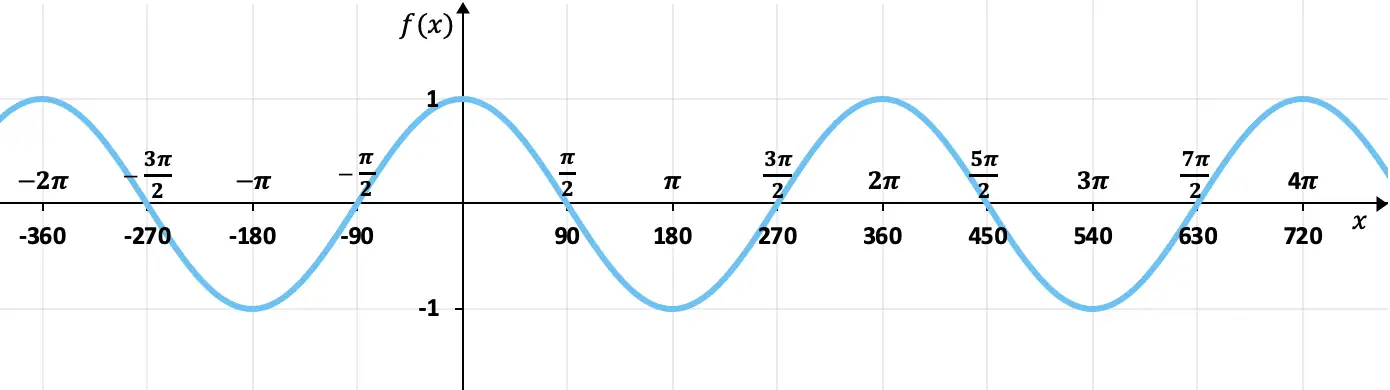
Diese Funktion entspricht der grafischen Darstellung einer trigonometrischen Funktion, genauer gesagt der Kosinusfunktion.
Wie wir der Grafik entnehmen können, wiederholt die Funktion ihre Werte periodisch, es handelt sich also um eine periodische Funktion. Darüber hinaus gibt es zwischen dem Höhepunkt und dem Höhepunkt der Welle einen Abstand von 2π (oder 360°), das ist also die Periode der Funktion.
![]()
Periodizität trigonometrischer Funktionen
Periodizität und trigonometrische Funktionen hängen eng zusammen. Tatsächlich besteht eines der Hauptmerkmale dieser Art von Funktionen darin, dass die meisten trigonometrischen Funktionen periodisch sind.
Als nächstes untersuchen wir die Periodizität der drei wichtigsten trigonometrischen Funktionen: Sinus, Cosinus und Tangens.
Periode der Sinusfunktion
Der Ausdruck für die Sinusfunktion lautet wie folgt:
![]()
In diesem Fall ist es nicht erforderlich, die Funktion grafisch darzustellen, um ihre Periode zu ermitteln, sondern sie kann einfach durch Anwendung der folgenden Formel berechnet werden:
![]()
Darüber hinaus hat die Sinusfunktion die Besonderheit, dass wir, wenn wir ihre Periode ändern, auch die Form ihres Diagramms ändern. Wie sich der Periodenwert auf seine grafische Darstellung auswirkt, können Sie im folgenden Link sehen:
➤ Siehe: Diagramm der Sinusfunktion
Periode der Kosinusfunktion
Der algebraische Ausdruck für die Kosinusfunktion lautet wie folgt:
![]()
Wie beim Sinus lässt sich die Periode der Kosinusfunktion direkt mit der folgenden Formel ermitteln:
![]()
Der Wert der Kosinusperiode bestimmt vollständig ihren Graphen. Klicken Sie auf den folgenden Link und finden Sie heraus, warum:
➤ Siehe: Graph der Kosinusfunktion
Periode der Tangensfunktion
Die Tangensfunktion wird mathematisch beschrieben:
![]()
Die Periode der Tangensfunktion wird nach der gleichen Formel berechnet wie die von Sinus und Cosinus:
![]()
Der Tangensfunktionsgraph unterscheidet sich jedoch von Sinus und Cosinus, da er auch Asymptoten aufweist, die sich periodisch wiederholen. Sie können diese und andere Funktionen dieser trigonometrischen Funktion unter dem folgenden Link sehen:
➤ Siehe: Graph der Tangensfunktion