Auf dieser Seite erklären wir, was ein perfektes quadratisches Trinom ist und wie es erklärt wird. Darüber hinaus können Sie sich mehrere Beispiele ansehen und Schritt-für-Schritt-Übungen zum perfekten quadratischen Trinom üben.
Was ist ein perfektes quadratisches Trinom?
Bevor Sie die Bedeutung eines perfekten quadratischen Trinoms verstehen, müssen Sie natürlich wissen, was Trinome sind. Ich empfehle daher, einen Blick auf diese verlinkte Seite zu werfen (wo alles ausführlich erklärt wird), bevor Sie fortfahren.
Die Definition eines perfekten quadratischen Trinoms lautet also wie folgt:
In der Mathematik ist ein perfektes quadratisches Trinom , auch TCP genannt, das Trinom, das man durch Quadrieren eines Binomials erhält.
Daher besteht ein perfektes quadratisches Trinom aus einem Polynom mit zwei perfekten Quadraten und einem weiteren Term, der das doppelte Produkt der Basen dieser Quadrate ist.

Wie Sie aus den beiden Formeln oben ersehen können, wird das perfekte quadratische Trinom aus zwei bemerkenswerten Identitäten (oder bemerkenswerten Produkten) erhalten, weshalb es so wichtig ist. Insbesondere wird ein perfektes quadratisches Trinom gefunden, wenn das Quadrat einer Addition oder das Quadrat einer Subtraktion gelöst wird.
Beispiele für perfekte quadratische Trinome
Um das Konzept des perfekten quadratischen Trinoms vollständig zu verstehen, erklären wir Schritt für Schritt zwei Beispiele:
Beispiel 1
![]()
Dieses Beispiel ist ein perfektes quadratisches Trinom, da es in seinem algebraischen Ausdruck zwei perfekte Quadrate gibt (d. h. sie haben eine exakte Quadratwurzel), da
![]()
und 9 sind äquivalent zu
![]()
und 3 jeweils zur Zweierpotenz erhoben:
![]()
![]()
Und mehr noch, das letzte verbleibende Glied des Trinoms
![]()
Man erhält es, indem man die Basen der beiden vorherigen Quadrate miteinander multipliziert und mit 2 multipliziert:
![]()
Die gesamte bemerkenswerte Identität in dieser Übung wäre also:
![]()
Beispiel 2
![]()
Auch dieses andere Beispiel ist ein perfektes quadratisches Trinom, da die drei notwendigen Bedingungen erfüllt sind: Zwei Terme entsprechen zwei perfekten Quadraten und ein weiterer Term ist das Ergebnis der Multiplikation der Basen dieser Quadrate miteinander und mit 2.
![]()
![]()
![]()
In diesem Fall hat das perfekte quadratische Trinom ein negatives Monom, es entspricht also der Entwicklung der bemerkenswerten Gleichheit einer quadrierten Differenz:
![]()
So faktorisieren Sie ein perfektes quadratisches Trinom
In der Algebra ist die Faktorisierung eines perfekten quadratischen Trinoms (PCT) ein sehr häufiges Problem. Falls Sie nicht wissen, was das bedeutet: Das Faktorisieren eines Polynoms bedeutet, seinen Ausdruck in ein Produkt von Faktoren umzuwandeln.
Um diese Art von algebraischem Trinom zu faktorisieren, müssen daher die folgenden Regeln beachtet werden:
- Das Trinom muss zwei perfekte Quadrate haben, die wir nennen werden
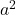
Und
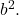
- Der dritte verbleibende Term des Trinoms muss gleich dem doppelten Produkt der Basen der beiden perfekten Quadrate sein, was mathematisch dem Ausdruck entspricht
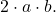
- Das faktorisierte Trinom wird sein
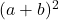
wenn alle Terme des perfekten quadratischen Trinoms positiv sind, andernfalls, wenn das Doppelprodukt der Basen der Quadrate ein negatives Vorzeichen hat, ist das faktorisierte Trinom
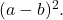
Um die Vorgehensweise vollständig zu verstehen, lösen wir eine Übung Schritt für Schritt:
- Faktorisieren Sie das folgende perfekte quadratische Trinom:
![]()
Als Erstes müssen wir feststellen, ob das Trinom zwei Elemente hat, die perfekte Quadrate sind, oder mit anderen Worten, ob seine Quadratwurzel keine Dezimalzahl ergibt. In diesem Problem
![]()
ist das Quadrat der Variablen
![]()
und 36 ist das Quadrat von 6:
![]()
![]()
Das Trinom hat also zwei perfekte Quadrate.
Zweitens müssen wir prüfen, ob der Zwischenterm dem im vorherigen Schritt berechneten Doppelprodukt der beiden Wurzeln entspricht:
![]()
Auch diese Regel wird eingehalten.
Dann sind alle Bedingungen erfüllt. Daher ist das faktorisierte perfekte quadratische Trinom das Binomial, das aus den beiden gefundenen Wurzeln gebildet wird (
![]()
und die Zahl 6) im Quadrat:
![]()
Da der Zwischenterm negativ ist, müssen wir auch ein Minuszeichen in Klammern setzen. Wenn es hingegen positiv wäre, müssten wir eine Summe hinzufügen:
![]()
Logischerweise ist die Faktorisierung ein komplizierter Vorgang. Daher empfehle ich Ihnen, zusätzlich zu den folgenden Übungen auch die folgenden Beispiele für die Faktorisierung von Polynomen anzusehen. In diesem Link erklären wir auch eine Methode, mit der man nicht nur Trinome, sondern auch jede Art von Polynom faktorisieren kann, und das genauso schnell.
Gelöste Übungen zum perfekten quadratischen Trinom
Wandeln Sie die folgenden Trinome in quadratische Binome um, indem Sie die entsprechende Formel anwenden:
![]()
![]()
![]()
![]()
![]()
Um ein perfektes quadratisches Trinom in die Potenz eines quadratischen Binomials umzuwandeln, müssen Sie die folgenden Formeln für die bemerkenswerten Identitäten des Quadrats einer Summe und des Quadrats einer Differenz verwenden:
![]()
![]()
Noch:
![]()
![]()
![]()
![]()
![]()
⬇⬇⬇ Vergessen Sie nicht, dass Sie uns alle Ihre Fragen unten in den Kommentaren schreiben können! ⬇⬇⬇