Parallele Ebenen

Auf dieser Seite finden Sie alles über parallele Ebenen: Wenn zwei Ebenen parallel sind, die Gleichungen zweier paralleler Ebenen, Beispiele, gelöste Aufgaben, Eigenschaften, …

Was sind zwei parallele Ebenen?

In der analytischen Geometrie sind zwei Ebenen parallel, wenn sie immer den gleichen Abstand voneinander haben. Daher schneiden sich zwei parallele Ebenen nie und haben nichts gemeinsam.

Zwei parallel liegende Ebenen sind nicht die einzig mögliche relative Position zwischen Ebenen, da sich zwei Ebenen im Raum (in R3) auch schneiden oder zusammenfallen können.

Woher wissen Sie, ob zwei Ebenen parallel sind?

Nachdem wir die Definition paralleler Ebenen kennengelernt haben, sehen wir uns nun an, wie Sie feststellen können, ob zwei Ebenen parallel sind oder nicht.

Ausgehend von der allgemeinen (oder impliziten) Gleichung zweier verschiedener Pläne:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

Die beiden Ebenen sind parallel, wenn ihre Koeffizienten A, B und C proportional zueinander und nicht zum Koeffizienten D sind. Mit anderen Worten liegt Parallelität zwischen zwei Ebenen vor, wenn die folgende Gleichung erfüllt ist:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

Beispiel für zwei parallele Ebenen

Beispielsweise sind die folgenden zwei Ebenen parallel:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

Die Pläne sind parallel, da die Koeffizienten der Variablen X, Y, Z zueinander proportional sind, nicht jedoch zu den unabhängigen Termen:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Berechnen Sie den Abstand zwischen zwei parallelen Ebenen

Zwei parallele Ebenen haben immer den gleichen Abstand voneinander. Um den Abstand zwischen zwei parallelen Ebenen zu ermitteln, können wir daher einen Punkt auf einer der beiden Ebenen nehmen und den Abstand von diesem Punkt zur anderen Ebene berechnen. Um den Abstand zwischen zwei parallelen Ebenen zu berechnen, ist es daher notwendig, die Formel für den Abstand von einem Punkt zu einer Ebene zu kennen.

Es ist eine Methode zum Ermitteln des Abstands zwischen zwei parallelen Ebenen. Es geht jedoch noch einfacher, wenn die Koeffizienten A, B und C der Gleichungen der beiden Ebenen übereinstimmen:

Betrachten Sie die allgemeinen (oder impliziten) Gleichungen zweier paralleler Ebenen:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

Die Formel zur Berechnung des Abstands zwischen zwei parallelen Ebenen lautet:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

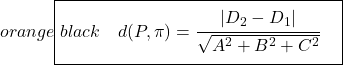
Daher ist es sicherlich einfacher, den Abstand zwischen zwei parallelen Ebenen mithilfe der Formel zu ermitteln, da es nur darum geht, die Formel anzuwenden, und das war’s, aber es kommt auf das Problem an. Darüber hinaus halten wir es für am besten, beide Methoden zur Entfernungsberechnung zu erklären, damit Sie die Methode auswählen können, die Ihnen am besten gefällt.

Beispiel für die Berechnung des Abstands zwischen zwei parallelen Ebenen

Als Beispiel berechnen wir den Abstand zwischen den folgenden zwei Ebenen:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Wir müssen zunächst überprüfen, ob es sich um zwei parallele Ebenen handelt. Somit sind alle Koeffizienten der Ebenengleichungen mit Ausnahme der unabhängigen Terme proportional, sodass es sich effektiv um zwei parallele Ebenen handelt.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In diesem Fall stimmen die Terme A, B und C der Gleichungen der beiden Ebenen nicht überein, aber wir können dies erreichen, indem wir die gesamte Gleichung der zweiten Ebene durch zwei teilen:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Die Gleichungen der beiden Ebenen haben nun also die gleichen Koeffizienten A, B und C. Daher können wir den Abstand zwischen den beiden Ebenen leicht mit der Formel für den Abstand zwischen zwei parallelen Ebenen berechnen:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Wir ersetzen die Werte und lösen die Operationen:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Damit ist der Abstand zwischen einer Ebene und der anderen Ebene gleich Eins.

Eigenschaften paralleler Ebenen

Die Eigenschaften paralleler Ebenen sind wie folgt:

Reflexive Eigenschaft : Jede Ebene ist parallel zu sich selbst.

$\pi_1 \parallel \pi_1$

Symmetrische Eigenschaft : Wenn eine Ebene parallel zu einer anderen ist, ist diese Ebene auch parallel zur ersten. Diese Eigenschaft besitzen auch senkrechte Ebenen.

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

Transitive Eigenschaft : Wenn eine Ebene parallel zu einer anderen Ebene ist und diese zweite Ebene parallel zu einer dritten Ebene ist, ist die erste Ebene auch parallel zur dritten Ebene.

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$