Parabel (Mathematik): Definition, Gleichung, Elemente, Beispiele,…

Auf dieser Seite finden Sie alles über die Parabel: Was sie ist, was sie darstellt, ihre Elemente (Brennpunkt, Leitlinie, Scheitelpunkt usw.), ihre Gleichung (mit den verschiedenen Gleichungstypen der Parabel), Beispiele, gelöste Übungen, seine Eigenschaften, seine Anwendungen, …

Was ist ein Gleichnis?

Die Parabel ist ein Konzept mit sehr unterschiedlichen Bedeutungen, ihre mathematische Definition lautet jedoch wie folgt:

In der Mathematik ist eine Parabel der Ort von Punkten auf der Ebene, die den gleichen Abstand von einem festen Punkt (genannt Fokus) und einer festen Linie (genannt Leitlinie) haben.

Daher hat jeder Punkt einer Parabel den gleichen Abstand von seinem Brennpunkt und seiner Leitlinie.

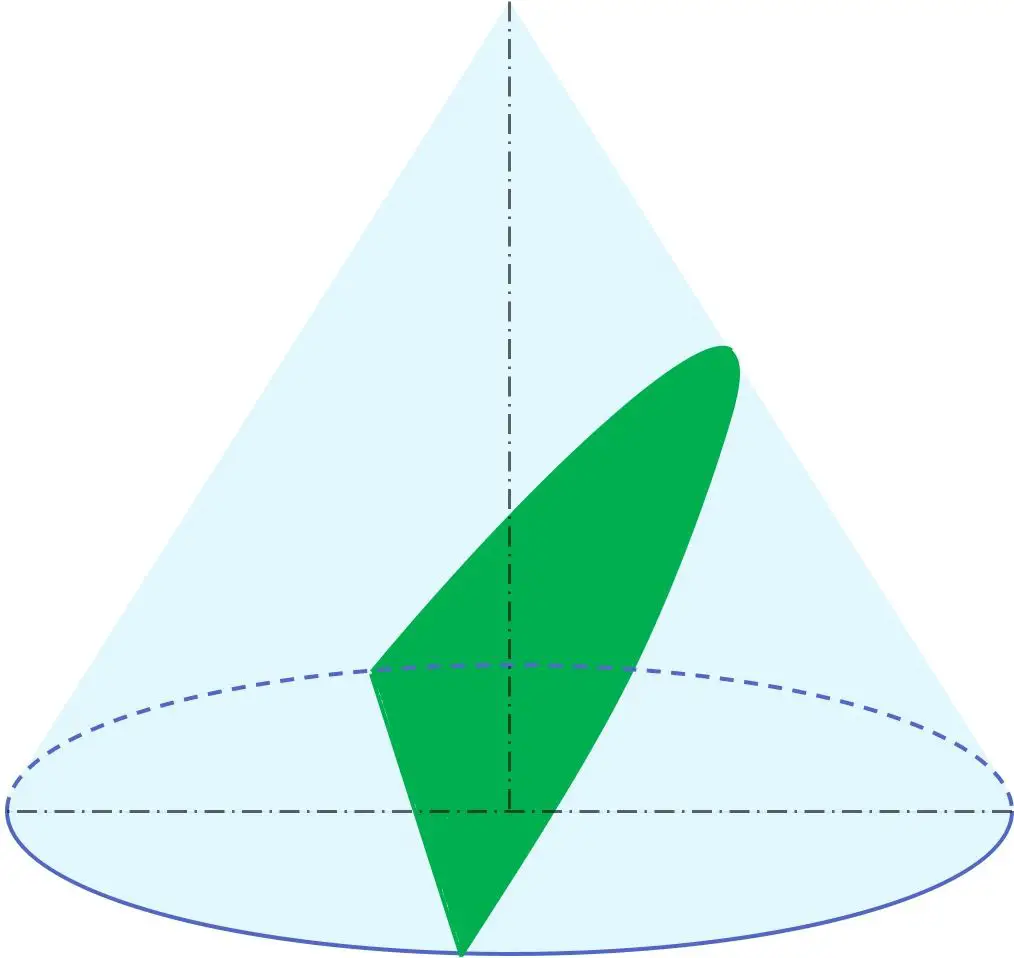
Darüber hinaus gehört die Parabel in der Geometrie neben Umfang, Ellipse und Hyperbel zu den Kegelschnitten. Mit anderen Worten, aus einem Kegel kann eine Parabel erhalten werden.

Insbesondere ergibt sich die Parabel aus dem Schnitt eines Kegels durch eine Ebene mit einem Neigungswinkel relativ zur Rotationsachse, der dem Winkel der Erzeugenden des Kegels entspricht. Daher ist die Ebene, die die Parabel enthält, parallel zum Generator des Kegels.

Elemente einer Parabel

Die Eigenschaften einer Parabel hängen von folgenden Elementen ab:

Fokus (F) : ist ein fester Punkt innerhalb der Parabel. Der Abstand von jedem Punkt der Parabel zum Brennpunkt ist gleich dem Abstand von demselben Punkt zur Leitlinie der Parabel.
Leitlinie (D) : Es handelt sich um eine feste Linie außerhalb der Parabel. Ein Punkt der Parabel hat von der Leitlinie den gleichen Abstand wie vom Brennpunkt der Parabel.
Parameter (p) : ist der Abstand vom Fokus zum Regisseur.
Radiusvektor (R) : ist das Segment, das einen Punkt der Parabel mit dem Fokus verbindet. Sein Wert stimmt mit dem Abstand vom Punkt zur Leitlinie überein.
Achse (E) : ist die Linie senkrecht zur Leitlinie, die durch den Fokus verläuft und die Symmetrieachse der Parabel ist, in der Grafik unten entspricht sie der Computerachse (Y-Achse). Auch Brennachse genannt.
Scheitelpunkt (V) : ist der Schnittpunkt zwischen der Parabel und ihrer Achse.
Brennweite : ist der Abstand zwischen dem Fokus und dem Scheitelpunkt oder zwischen der Leitlinie und dem Scheitelpunkt. Sein Wert ist immer gleich
$\displaystyle \frac{p}{2}.$

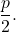
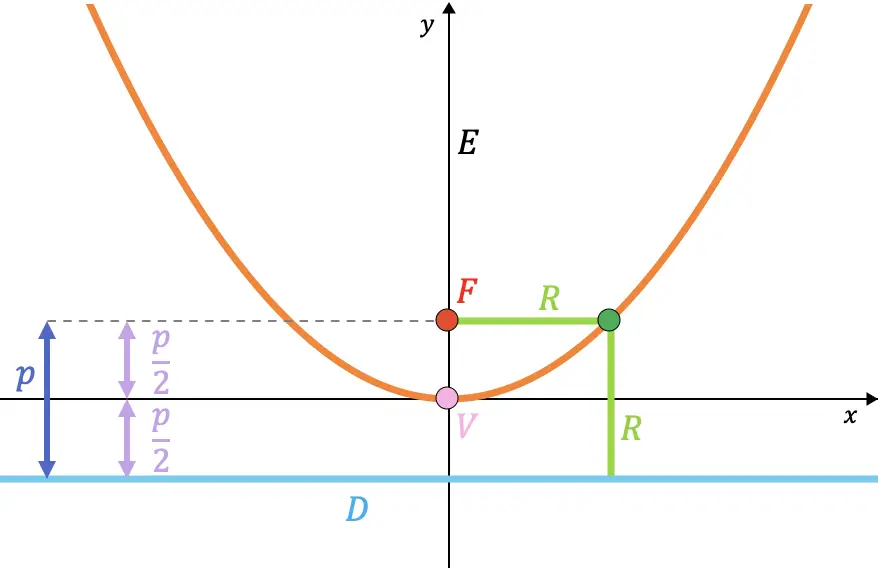
rechte Seite

Die rechte Seite einer Parabel ist die Sehne innerhalb der Parabel, die durch den Brennpunkt verläuft und parallel zur Leitlinie verläuft.

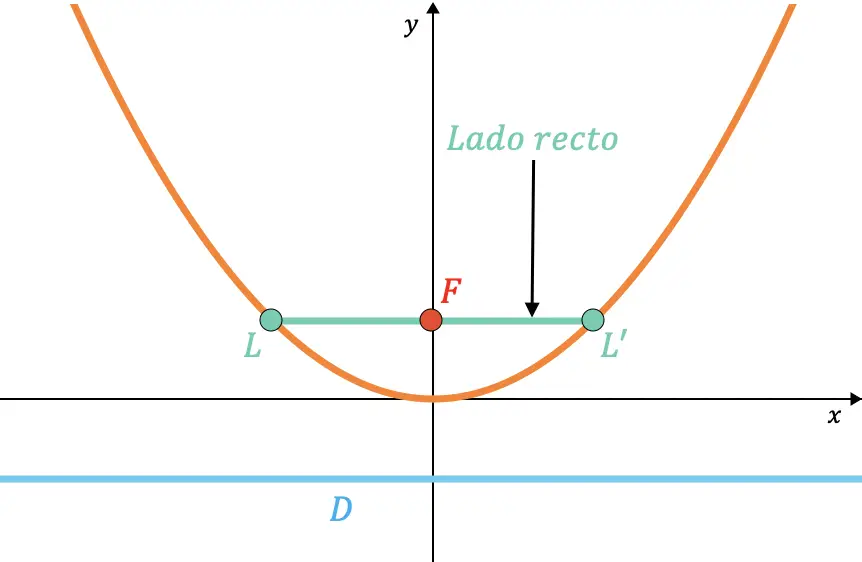
Ebenso lässt sich zeigen, dass die Länge der rechten Seite immer doppelt so groß ist wie der Wert des Parameters

$p.$

$\lvert LL'\rvert = 2p$

Andererseits bilden die beiden Tangenten der Parabel, die durch die Enden der rechten Seite verlaufen, einen 45°-Winkel mit der rechten Seite selbst und schneiden sich auch am oberen Ende der Parabel.

Parabelgleichungen

Die Parabelgleichung ist eine Art quadratische Funktion, da sie immer mindestens einen quadratischen Term haben muss. Darüber hinaus hängt die Gleichung einer Parabel von ihrer horizontalen oder vertikalen Ausrichtung ab.

Daher gibt es in der analytischen Geometrie mehrere Möglichkeiten, eine Parabel mathematisch auszudrücken: die kanonische oder reduzierte Gleichung , die gewöhnliche Gleichung und die allgemeine Gleichung der Parabel.

Reduzierte oder kanonische Gleichung der Parabel

Was die reduzierte oder kanonische Gleichung von anderen parabolischen Gleichungen unterscheidet, besteht darin, dass der Scheitelpunkt der Parabel der Koordinatenursprung ist , also der Punkt (0,0).

Die Form der reduzierten Parabelgleichung hängt davon ab, ob sie horizontal oder vertikal ist. Schauen Sie sich die folgende grafische Darstellung an, in der die 4 möglichen Varianten angegeben sind:

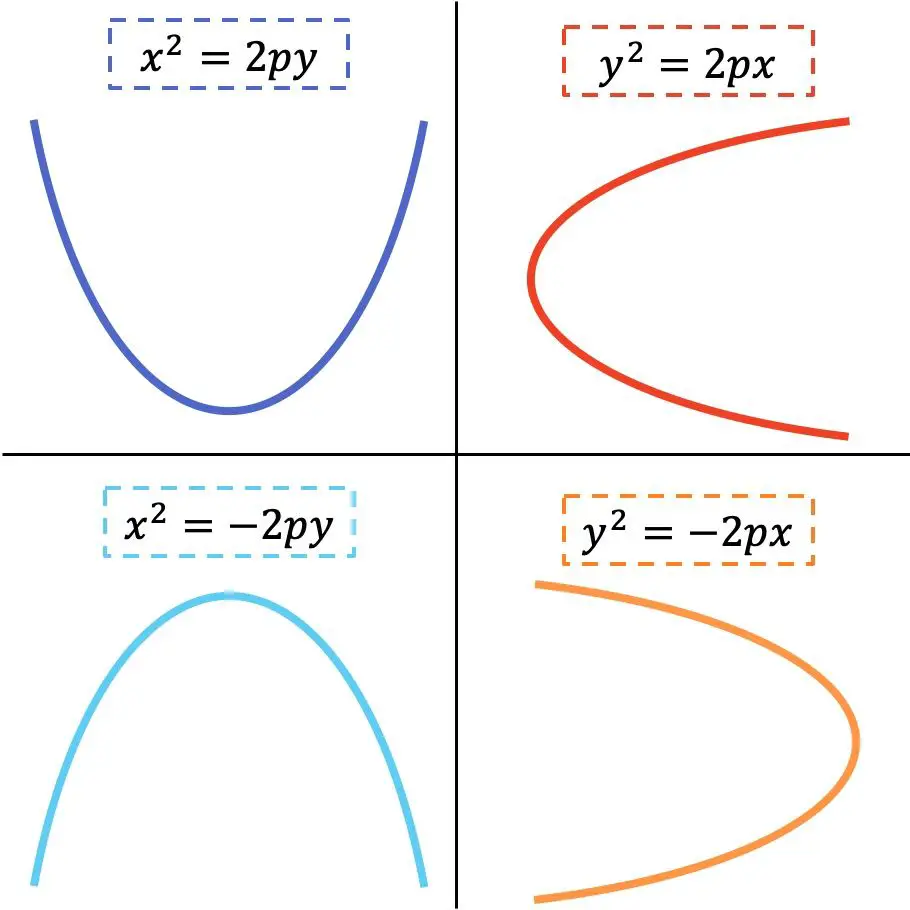
Gold

$p$

ist der charakteristische Parameter der Parabel.

Wie Sie im vorherigen Bild sehen können, ist die Parabel vertikal, wenn die Variable x quadriert wird. Wenn dagegen die Variable y quadriert wird, ist die Parabel horizontal. Andererseits hängt die Richtung der Parabeläste vom Vorzeichen der Gleichung ab.

Gewöhnliche Gleichung der Parabel

Wir haben gerade gesehen, wie die Gleichung der Parabel aussieht, wenn ihr Scheitelpunkt oder Mittelpunkt dem Koordinatenursprung entspricht (die reduzierte oder kanonische Gleichung), aber wie lautet die Gleichung der Parabel, wenn der Scheitelpunkt außerhalb des Ursprungs liegt?

Wenn der Scheitelpunkt der Parabel ein beliebiger Punkt ist, verwenden wir die gewöhnliche Gleichung der Parabel , deren Ausdruck lautet:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

wobei der Mittelpunkt oder Scheitelpunkt der Parabel der Punkt ist

$V(x_0,y_0).$

Die vorherige Gleichung entspricht der vertikal ausgerichteten Parabel, d. h. die Brennachse der Parabel verläuft parallel zur Y-Achse.

Ebenso müssen wir zur Definition einer horizontal ausgerichteten Parabel (ihre Brennachse verläuft parallel zur X-Achse) die folgende Variante der gewöhnlichen Parabelgleichung verwenden:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

Wobei, wie zuvor, der Mittelpunkt oder Scheitelpunkt der Parabel der Punkt ist

$V(x_0,y_0).$

Allgemeine Gleichung der Parabel

Bisher werden alle Parabelgleichungen, die wir analysiert haben, verwendet, um horizontale oder vertikale Parabeln auszudrücken. Aber natürlich kann eine Parabel auch schief oder geneigt sein .

Nun, um diese Art von Parabel auszudrücken, verwenden wir die allgemeine Parabelgleichung , deren Formel wie folgt lautet:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

Die obige Gleichung ist genau dann eine Parabel, wenn die Koeffizienten

$A$

Und

$C$

nicht gleichzeitig Null sind und darüber hinaus folgende Bedingung erfüllt ist:

$B^2-4AC =0$

Beispiel dafür, wie man den Scheitelpunkt, den Fokus und die Leitlinie einer Parabel aus ihrer Gleichung ermittelt

In vielen Parabelübungen und -aufgaben werden Sie gebeten, den Scheitelpunkt, den Fokus und die Leitlinie einer bestimmten Parabel zu berechnen. Sehen wir uns daher anhand eines Beispiels an, wie dies geschieht:

Finden Sie den Scheitelpunkt, den Fokus und die Leitlinie der folgenden Parabel:

$x^2 = 4y$

Die grundlegende Lösung dieses Parabelproblems ist die Bestimmung des Parameters p der Parabel . In diesem Fall entspricht die Gleichung der Parabel der reduzierten oder kanonischen Gleichung (vertikale Parabel):

$x^2 = 2py$

Daher ist der Parameter p :

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

Da die Parabel andererseits der reduzierten oder kanonischen Gleichung folgt, bedeutet dies, dass ihr Scheitelpunkt oder Mittelpunkt im Koordinatenursprung liegt:

$\bm{V(0,0)}$

Sobald wir den Scheitelpunkt und den Parameterwert der Parabel kennen, können wir leicht ihren Fokus und ihre Leitlinie ermitteln.

Der quadratische Term der Gleichung ist die Variable x , so dass die Achse der Parabel parallel zur Achse OY verläuft und tatsächlich, da ihr Scheitelpunkt der Punkt (0,0) ist, die Achse der Parabel die Achse OY sein wird Achse selbst. Dann liegt der Brennpunkt einer Parabel immer auf der Achse der Parabel und im Abstand von

$p/2$

von der Spitze der Parabel, daher sind ihre Koordinaten:

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

Ebenso ist die Hilfslinie die horizontale Linie, die sich in einiger Entfernung befindet

$p/2$

vom Scheitelpunkt der Parabel, dem Ursprung der Koordinaten. Die Geradengleichung lautet daher:

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

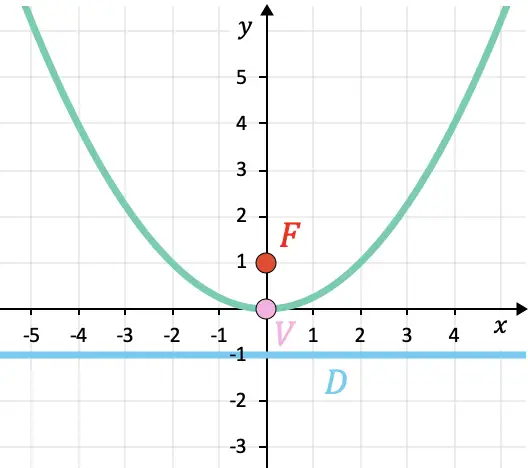
Die Parabel wurde unten grafisch dargestellt, damit Sie die Ergebnisse überprüfen können:

Eigenschaften von Parabeln

Alle Parabeln haben folgende Eigenschaften:

Eine Parabel ist eine offene Kurve, das heißt, sie besteht aus zwei Ästen ohne gemeinsame Punkte, die sich unbegrenzt erstrecken.
Jede Parabel hat eine einzigartige Symmetrieachse, auf der sich der Scheitelpunkt der Parabel befindet.
Eine vertikal ausgerichtete Parabel ist konvex, wenn ihre Äste nach oben zeigen; im Gegenteil, die Parabel ist konkav, wenn ihre Äste nach unten verlaufen.
Die Exzentrizität einer Parabel entspricht Eins (1). Die Exzentrizität ist ein Koeffizient, der in diesem Fall berechnet wird, indem man den Abstand vom Brennpunkt zum Mittelpunkt der Parabel durch den Abstand vom Scheitelpunkt zur Leitlinie dividiert (und die beiden Abstände stimmen in ihrem Wert immer überein).
Aus der vorherigen Eigenschaft folgt, dass alle Parabeln ähnlich oder ähnlich sind.
Eine Parabel hat keine Asymptoten.

parabolische Anwendungen

Da Sie nun mit der Bedeutung eines Gleichnisses bestens vertraut sind, fragen Sie sich vielleicht: „Was ist der Sinn eines Gleichnisses?“

Nun, auch wenn es Ihnen nicht so vorkommt, ist die geometrische Form einer Parabel im wirklichen Leben sehr verbreitet. Beispielsweise führt ein Ball beim Werfen häufig eine parabolische Bewegung aus, insbesondere beim Basketball. Nun, die Parabelgleichung ist sehr nützlich für die analytische Untersuchung der parabelförmigen Bahn, der der Ball folgt.

Eine weitere Anwendung der Schüssel betrifft Antennen (daher der Name Parabolantenne). Da jeder Strahl, der auf ein parabolisch geformtes Objekt parallel zur Symmetrieachse fällt, direkt zum Fokus reflektiert wird, werden alle Strahlen, die zur Parabolantenne gelangen, im Fokus konzentriert, was auf unterschiedliche Weise genutzt werden kann. Deshalb ist der Schwerpunkt eines Gleichnisses so wichtig.

Probleme mit Gerichten behoben

Übung 1

Berechnen Sie den Scheitelpunkt, den Brennpunkt und die Leitlinie der Parabel, deren Gleichung wie folgt lautet:

$y^2 = 8x$

siehe Lösung

Erstens ist die Parabel horizontal, da sie dem folgenden Ausdruck der reduzierten oder kanonischen Gleichung der Parabel folgt:

$y^2 = 2px$

Sein Parameter p ist also:

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

Da die Parabel andererseits der reduzierten oder kanonischen Gleichung folgt, bedeutet dies, dass ihr Scheitelpunkt oder Mittelpunkt im Koordinatenursprung liegt:

$\bm{V(0,0)}$

Sobald wir den Scheitelpunkt und den Parameterwert der Parabel kennen, können wir ihren Fokus und ihre Leitlinie leicht berechnen.

Der quadratische Term der Gleichung ist die Variable und das heißt, die Achse der Parabel wird parallel zur OX-Achse sein und tatsächlich, da ihr Scheitelpunkt der Punkt (0,0) ist, wird l die Achse der Parabel sein die OX-Achse selbst. Dann liegt der Brennpunkt einer Parabel immer auf der Achse der Parabel und im Abstand von

$p/2$

von der Spitze der Parabel, deren Koordinaten sind:

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

Ebenso liegt die Leitlinie auf Distanz

$p/2$

vom Scheitelpunkt der Parabel, der den Koordinatenursprung darstellt und senkrecht zu ihrer Brennachse steht. Die Gleichung der Richtgeraden lautet daher:

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

Übung 2

Finden Sie den Scheitelpunkt, den Fokus und die Leitlinie der Parabel, deren Gleichung wie folgt lautet:

$(x-4)^2 = -16(y+1)$

siehe Lösung

Die Parabel wird gemäß ihrer gewöhnlichen Gleichung (Achse parallel zur Y-Achse) definiert, deren Formel lautet:

$(x-x_0 )^2 = 2p (y-y_0)$

Sein Parameter p ist also:

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

Andererseits impliziert in diesem Fall die gewöhnliche Gleichung der Parabel, dass ihr Mittelpunkt nicht im Koordinatenursprung liegt. Andererseits sind die kartesischen Koordinaten des Scheitelpunkts der Parabel die Zahlen in Klammern mit geändertem Vorzeichen :

$\bm{V(4,-1)}$

Sobald wir den Scheitelpunkt und den Parameterwert der Parabel kennen, können wir ihren Fokus und ihre Leitlinie berechnen.

Der quadratische Term der Gleichung ist die Variable x , sodass die Achse der Parabel parallel zur Achse OY verläuft. Somit liegt der Brennpunkt einer Parabel immer auf der Achse der Parabel und im Abstand von

$p/2$

vom Scheitelpunkt der Parabel, so dass die Brennpunktkoordinaten durch Addition denen des Scheitelpunkts entsprechen

$p/2$

vertikal:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

Ebenso ist die Leitlinie die in einiger Entfernung liegende horizontale Linie

$p/2$

von der Spitze der Parabel. Die Gleichung der Richtgeraden lautet daher:

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

Übung 3

Bestimmen Sie die Parabelgleichung, deren Achse parallel zur Abszissenachse verläuft, deren Scheitelpunkt der Punkt V(5,2) ist und deren Mittelpunkt der Punkt P(8,2) ist.

siehe Lösung

In diesem Fall ist der Scheitelpunkt der Parabel nicht der Ursprung der Koordinaten, daher benötigen wir die gewöhnliche Gleichung, um die Parabel der Aussage zu definieren. Außerdem verläuft die Brennachse der Parabel parallel zur x-Achse, was bedeutet, dass die Parabel horizontal ausgerichtet ist (die Zweige verlaufen nach rechts oder links) und daher der quadratische Term der Gleichung die Variable sein muss y :

$(y-y_0 )^2 = 2p (x-x_0)$