Hier erklären wir, wie Funktionsoptimierungsprobleme schrittweise gelöst werden. Darüber hinaus haben Sie die Möglichkeit, anhand von Übungsaufgaben zu Optimierungsproblemen zu üben.
Was sind Optimierungsprobleme?
Optimierungsprobleme sind Probleme, bei denen es darum geht, das Maximum oder Minimum einer Funktion zu finden. Ein Optimierungsproblem würde beispielsweise darin bestehen, das Maximum einer Funktion zu berechnen, die den Gewinn eines Unternehmens definiert.
So lösen Sie Optimierungsprobleme
Schritte zur Lösung von Funktionsoptimierungsproblemen:
- Legen Sie die Funktion fest , die optimiert werden muss.
- Leiten Sie die zu optimierende Funktion ab.
- Finden Sie die kritischen Punkte der zu optimierenden Funktion. Dazu müssen Sie die Ableitung der Funktion gleich Null setzen und die resultierende Gleichung lösen.
- Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Beispiel für ein Optimierungsproblem
Unter Berücksichtigung der Theorie der Optimierungsprobleme werden wir ein Problem dieser Art Schritt für Schritt lösen, damit Sie sehen können, wie es ausgeführt wird.
- Berechnen Sie unter allen rechtwinkligen Dreiecken, deren Schenkel insgesamt 10 cm lang sind, die Abmessungen des Dreiecks mit der größten Oberfläche.
Um das Problem zu lösen, nennen wir einen Zweig des Dreiecks x und den anderen Zweig y :

Schritt 1: Stellen Sie die zu optimierende Funktion ein.
Wir möchten, dass die Fläche des Dreiecks maximal ist, und die Formel für die Fläche eines Dreiecks lautet:
![]()
In unserem Fall ist die Basis des Dreiecks x und seine Höhe ist y . Noch:
![]()
Wir haben bereits die Funktion zur Optimierung, aber sie hängt von zwei Variablen ab, während sie nur von einer abhängen kann. Allerdings besagt die Aussage, dass die beiden Beine insgesamt 10 cm lang sein müssen. Noch:
![]()
Wir lösen nach y aus dieser Gleichung auf:
![]()
Und wir ersetzen den Ausdruck in der Funktion:
![]()
![]()
Jetzt haben wir die geplante Optimierungsfunktion und sie hängt nur von einer Variablen ab, sodass wir mit dem nächsten Schritt fortfahren können.
Schritt 2: Berechnen Sie die Ableitung der zu optimierenden Funktion.
Da es sich um eine rationale Funktion handelt, wenden wir die Formel für die Ableitung der Division an, um sie abzuleiten:
![]()
![]()
Schritt 3: Finden Sie die kritischen Punkte.
Um die kritischen Punkte der Funktion zu finden, müssen wir die Ableitung gleich Null setzen und die resultierende Gleichung lösen:
![]()
![]()
Die 4 teilt die gesamte linke Seite, sodass wir sie multiplizieren können, indem wir die gesamte rechte Seite multiplizieren:
![]()
![]()
![]()
![]()
![]()
Schritt 4: Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Um die Monotonie der Funktion zu untersuchen, stellen wir den kritischen Punkt rechts dar:
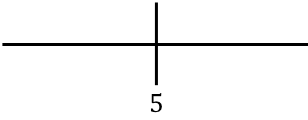
Und jetzt bewerten wir das Vorzeichen der Ableitung in jedem Intervall, um herauszufinden, ob die Funktion zunimmt oder abnimmt. Dazu nehmen wir einen Punkt in jedem Intervall (niemals den kritischen Punkt) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:
![]()
![]()
![]()
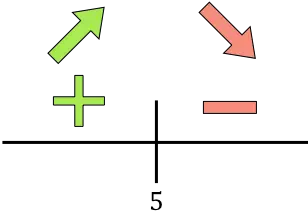
Wenn die Ableitung positiv ist, bedeutet dies, dass die Funktion zunimmt, und wenn die Ableitung negativ ist, bedeutet dies, dass die Funktion abnimmt. Daher sind die Intervalle zum Erhöhen und Verringern der Funktion:
Wachstum:
![]()
Verringern:
![]()
Bei x=5 geht die Funktion von steigender zu fallender Funktion über, sodass x=5 ein relatives Maximum der zu optimierenden Funktion ist .
Daher ist x=5 der Wert des Dreieckszweigs, der die größte Fläche hat. Berechnen Sie einfach den Wert des anderen Beins:
![]()
Zusammenfassend sind die Werte, die die maximale Fläche des Dreiecks maximieren:
![]()
![]()
Optimierungsprobleme behoben
Problem 1
Das Arzneimittel wird einer kranken Person verabreicht und
![]()
Einige Stunden später ist die Blutkonzentration des Wirkstoffs durch die Funktion gegeben
![]()
Milligramm pro Milliliter. Bestimmen Sie den Maximalwert von
![]()
und zeigt an, wann dieser Wert erreicht ist.
Schritt 1: Stellen Sie die zu optimierende Funktion ein.
In diesem Problem geben sie uns bereits die vorgeschlagene Funktion, nämlich
![]()
Schritt 2: Berechnen Sie die Ableitung der zu optimierenden Funktion.
Die Funktion setzt sich aus dem Produkt zweier Funktionen zusammen. Um die Ableitung der Funktion zu berechnen, müssen wir daher die Regel für die Ableitung eines Produkts anwenden:
![]()
![]()
Schritt 3: Finden Sie die kritischen Punkte.
Um die kritischen Punkte der Funktion zu finden, lösen wir
![]()
![]()
![]()
Wir nehmen den gemeinsamen Faktor, um die Gleichung zu lösen:
![]()
Damit die Multiplikation gleich 0 ist, muss eines der beiden Elemente der Multiplikation Null sein. Deshalb setzen wir jeden Faktor gleich 0:
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
Eine Zahl, die auf eine andere Zahl erhöht wird, kann daher niemals 0 ergeben.
![]()
Es gibt keine Lösung.
Schritt 4: Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Um die Monotonie der Funktion zu untersuchen, stellen wir den kritischen Punkt rechts dar:
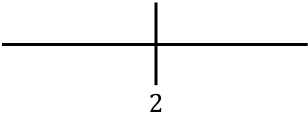
Und jetzt bewerten wir das Vorzeichen der Ableitung in jedem Intervall, um herauszufinden, ob die Funktion zu- oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals den kritischen Punkt) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:
![]()
![]()
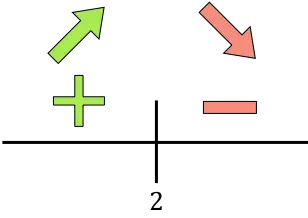
Wenn die Ableitung positiv ist, bedeutet dies, dass die Funktion zunimmt. Ist die Ableitung hingegen negativ, bedeutet dies, dass die Funktion abnimmt. Somit betragen die Wachstums- und Abfallintervalle der zu optimierenden Funktion:
Wachstum:
![]()
Verringern:
![]()
Die Funktion geht bei t=2 vom Ansteigenden zum Absteigenden über, daher ist t=2 ein Maximum der Funktion. Die maximale Konzentration wird daher in t=2 Stunden erreicht.
Schließlich setzen wir den Wert, bei dem das Maximum auftritt, in die ursprüngliche Funktion ein, um den Wert der maximalen Konzentration zu ermitteln:
![]()
Problem 2
Ein Geschäft hofft, 40 Elektroroller zu einem Preis von 1.000 Euro pro Roller verkaufen zu können. Aber laut Marktforschung führt jede Reduzierung des Rollerpreises um 50 Euro zu einem Anstieg der Verkäufe der Top 10 der meistverkauften Roller.
Schreiben Sie zunächst die Umsatzfunktion des Geschäfts basierend auf der Häufigkeit, mit der der ursprüngliche Preis des Rollers von 1.000 US-Dollar um 50 US-Dollar gesenkt wird. Bestimmen Sie als Nächstes den Preis des Rollers, um den maximalen Gewinn und den mit diesem Preis erzielten Umsatz zu erzielen.
Schritt 1: Stellen Sie die zu optimierende Funktion ein.
Die Problemstellung gibt uns einen Hinweis, da sie uns sagt, dass die Funktion davon abhängen muss, wie oft der Anfangspreis um 50 $ reduziert wird. Wir nennen daher x die Häufigkeit, mit der der Preis um 50 € gesenkt wird:
![]()
€
Die Umsatzfunktion ist die Anzahl der verkauften Roller multipliziert mit dem Preis jedes Rollers:
![]()
Die Anzahl der verkauften Roller beträgt 40 plus 10 Roller für jeweils 50 € Preisnachlass. Noch:
![]()
Der Preis für jeden Roller beträgt zu Beginn 1.000 € und sinkt mit jeder Preissenkung um 50 €. Noch:
![]()
Die Funktion zur Optimierung des Problems lautet daher:
![]()
![]()
![]()
![]()
Schritt 2: Berechnen Sie die Ableitung der zu optimierenden Funktion.
Da es sich um eine Polynomfunktion handelt, ist die Ableitung einfacher zu berechnen:
![]()
Schritt 3: Finden Sie die kritischen Punkte der Funktion.
Um die kritischen Punkte der Funktion zu finden, lösen wir
![]()
![]()
![]()
![]()
![]()
Schritt 4: Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Um die Monotonie der Funktion zu untersuchen, stellen wir den auf der Zahlengeraden berechneten kritischen Punkt dar:
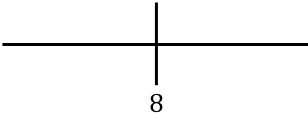
Und jetzt bewerten wir das Vorzeichen der Ableitung in jedem Intervall, um herauszufinden, ob die Funktion zu- oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals den kritischen Punkt) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:
![]()
![]()
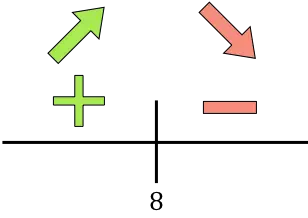
Wenn die Ableitung positiv ist, bedeutet dies, dass die Funktion zunimmt, und wenn die Ableitung negativ ist, bedeutet dies, dass die Funktion abnimmt. Daher sind die Wachstums- und Rückgangsintervalle:
Wachstum:
![]()
Verringern:
![]()
Die Funktion geht bei x=8 vom Ansteigenden zum Absteigenden über, sodass x=8 ein Maximum der Funktion ist . Daher wird das maximale Einkommen durch die 8-fache Ermäßigung von 50 € erzielt.
Wir setzen nun den Wert, bei dem das maximale Einkommen erscheint, in die ursprüngliche Funktion ein, um den Wert des maximalen Einkommens zu ermitteln:
![]()
![]()
€
Und der Preis für jeden Roller beträgt nach achtmaligem Inanspruchnahme des Rabatts von 50 €:
![]()
![]()
€
Problem 3
Die Kostenfunktion (in Tausend Euro) eines Unternehmens kann mit folgendem Ausdruck ermittelt werden:
![]()
Gold
![]()
stellt die Tausenden von produzierten Einheiten eines bestimmten Artikels dar.
Bestimmen Sie, wie viel produziert werden muss, damit die Kosten minimal sind, wie hoch diese Kosten sind und wie hoch die Kosten wären, wenn keiner dieser Artikel produziert würde.
Schritt 1: Stellen Sie die zu optimierende Funktion ein.
Die Problemstellung liefert uns bereits die zu optimierende Funktion
![]()
Schritt 2: Berechnen Sie die Ableitung der zu optimierenden Funktion.
![]()
Schritt 3: Finden Sie die kritischen Punkte.
Um die kritischen Punkte der Funktion zu finden, lösen wir
![]()
![]()
![]()
![]()
![]()
Schritt 4: Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Wir stellen den kritischen Punkt rechts dar:
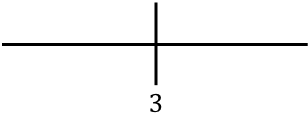
Und jetzt bewerten wir das Vorzeichen der Ableitung in jedem Intervall, um herauszufinden, ob die Funktion zu- oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals den kritischen Punkt) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:
![]()
![]()
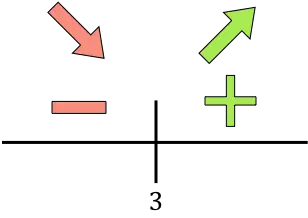
Wenn die Ableitung größer als Null ist, nimmt die Funktion über dieses Intervall zu. Ist die Ableitung hingegen kleiner als Null, nimmt die Funktion in diesem Intervall ab. Somit sind die Intervalle der Zunahme und Abnahme der Funktion:
Wachstum:
![]()
Verringern:
![]()
Die Funktion geht bei x=3 von abnehmend zu steigend über, sodass x=3 ein Minimum der Funktion ist . Daher werden die minimalen Kosten durch die Produktion von 3.000 Einheiten erreicht.
Wir setzen nun den Wert, bei dem die Mindestkosten erreicht werden, in die ursprüngliche Funktion ein, um den Mindestkostenwert zu ermitteln:
![]()
Millionen Euro.
Andererseits fragen sie uns, wie hoch die Kosten wären, wenn nichts produziert würde, also wann
![]()
Daher ist eine Berechnung erforderlich
![]()
![]()
Millionen Euro.
Problem 4
Wir wollen einen rechteckigen Holzrahmen bauen, der eine Fläche von 2 m 2 abgrenzt. Wir wissen, dass der Holzpreis für horizontale Seiten 7,5 €/m und für vertikale Seiten 12,5 €/m beträgt. Bestimmen Sie die Abmessungen, die das Rechteck haben muss, damit die Gesamtkosten des Rahmens so gering wie möglich sind und dass diese Kosten minimal sind.
Schritt 1: Stellen Sie die zu optimierende Funktion ein.
Um das Problem zu lösen, nennen wir die horizontale Seite x und die vertikale Seite y :

Der Kauf einer horizontalen Seite kostet 7,5 € und der Kauf einer vertikalen Seite kostet 12,5 €. Zusätzlich benötigen wir für jeden Rahmen zwei horizontale Seiten und zwei vertikale Seiten. Daher können die Kosten des Rahmens mit der folgenden Funktion ermittelt werden:
![]()
Wir haben bereits die Funktion zur Optimierung. Aber es hängt von zwei Variablen ab, wenn es nur von einer abhängen kann. Allerdings besagt die Aussage, dass die Fläche des Rahmens 2 m 2 betragen muss. Noch:
![]()
Wir löschen die Variable y :
![]()
Und wir ersetzen den Ausdruck, der in der zu optimierenden Funktion gefunden wird:
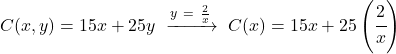
![]()
Schritt 2: Berechnen Sie die Ableitung der zu optimierenden Funktion.
![]()
Schritt 3: Finden Sie die kritischen Punkte.
Um die kritischen Punkte der Funktion zu finden, lösen wir
![]()
![]()
![]()
![]()
![]()
![]()
Wir multiplizieren transversal, um die Gleichung mit Brüchen zu lösen:
![]()
![]()
![]()
![]()
![]()
Schritt 4: Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Wir stellen den kritischen Punkt dar, der zur Analyse der Monotonie der Funktion auf der Geraden gefunden wurde:
Und jetzt bewerten wir das Vorzeichen der Ableitung in jedem Intervall, um herauszufinden, ob die Funktion zu- oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals den kritischen Punkt) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:
![]()
![]()
Wenn die Ableitung positiv ist, bedeutet dies, dass die Funktion zunimmt, und wenn die Ableitung negativ ist, bedeutet dies, dass die Funktion abnimmt. Daher sind die Wachstums- und Rückgangsintervalle:
Wachstum:
![]()
Verringern:
![]()
Die Funktion wechselt bei x=1,83 von fallend zu steigend, sodass x=1,83 ein Minimum der Funktion ist .
Daher ist x=1,83 der Wert der horizontalen Seite, der die minimalen Kosten darstellt. Berechnen wir nun den Wert der vertikalen Seite:
![]()
Somit sind die Werte, die die minimalen Rahmenkosten ausmachen:
horizontale Seite
![]()
vertikale Seite
![]()
Und die mit diesen Werten erreichten Mindestkosten betragen:
![]()
€
Problem 5
Die Tür einer Kathedrale besteht aus einem halb umlaufenden Bogen, der von zwei Säulen getragen wird, wie in der folgenden Abbildung dargestellt:
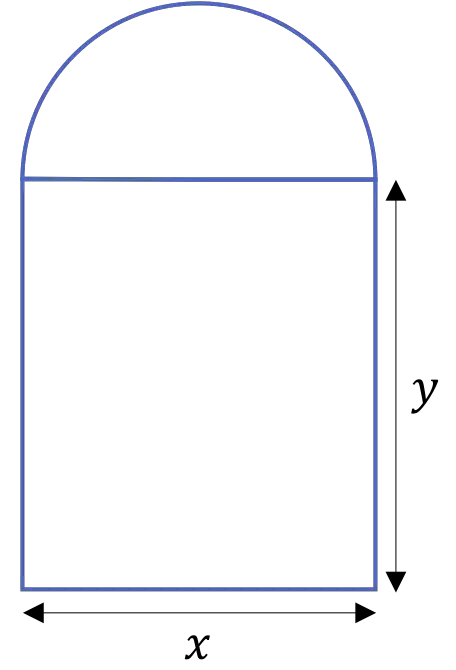
Wenn der Umfang der Tür 20 m beträgt, ermitteln Sie die Maße
![]()
Und
![]()
wodurch die Oberfläche der gesamten Tür maximiert wird.
Schritt 1: Stellen Sie die zu optimierende Funktion ein.
Die Fläche eines Kreises wird mit der Formel berechnet
![]()
Die Fläche der gesamten Tür ist also die Fläche des Rechtecks plus die Hälfte der Umfangsfläche:
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
Wir haben bereits die Funktion zur Optimierung. Aber es hängt von zwei Variablen ab, wenn es nur von einer abhängen kann.
Aus der Pressemitteilung geht jedoch hervor, dass der Umfang des gesamten Tors 20 m beträgt. Der Umfang eines Kreises wird mit der Formel berechnet
![]()
Daher beträgt der Umfang der gesamten Tür:
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
Der Umfang muss 20 m betragen. Wir setzen daher den vorherigen Ausdruck auf 20, um die Beziehung zwischen zu finden
![]()
Und
![]()
![]()
Wir multiplizieren alle Terme mit 2, um Brüche zu eliminieren:
![]()
![]()
Wir klären
![]()
![]()
![]()
Und wir ersetzen den Ausdruck, der in der zu optimierenden Funktion gefunden wird:
![]()
![]()
![]()
Schritt 2: Berechnen Sie die Ableitung der zu optimierenden Funktion.
![]()
![]()
Schritt 3: Finden Sie die kritischen Punkte.
Um die kritischen Punkte der Funktion zu finden, lösen wir
![]()
![]()
![]()
Da es sich um eine Gleichung mit Brüchen handelt, multiplizieren wir jeden Term mit dem lcm der Nenner, um die Brüche zu eliminieren:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Schritt 4: Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Um die Monotonie der Funktion zu untersuchen, stellen wir den kritischen Punkt rechts dar:
Und jetzt bewerten wir das Vorzeichen der Ableitung in jedem Intervall, um herauszufinden, ob die Funktion zu- oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals den kritischen Punkt) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:
![]()
![]()
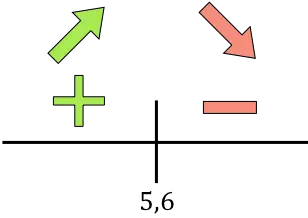
Wenn die Ableitung positiv ist, bedeutet dies, dass die Funktion zunimmt, und wenn die Ableitung negativ ist, bedeutet dies, dass die Funktion abnimmt. Daher sind die Wachstums- und Rückgangsintervalle:
Wachstum:
![]()
Verringern:
![]()
Die Funktion geht bei x=5,6 vom Ansteigenden zum Absteigenden über, sodass x=5,6 ein Maximum der Funktion ist .
Noch,
![]()
ist der Wert, der die maximale Oberfläche ergibt. Jetzt berechnen wir den Wert von
![]()
![]()
Somit sind die Werte, aus denen sich die maximale Oberfläche zusammensetzt:
![]()
![]()
Problem 6
Wir wollen einen zylinderförmigen Tank mit einer Fläche von 54 cm 2 bauen. Bestimmen Sie den Radius der Grundfläche und die Höhe des Zylinders so, dass das Volumen maximal ist.
Schritt 1: Stellen Sie die zu optimierende Funktion ein.
Das Volumen eines Zylinders wird mit der folgenden Formel berechnet:
![]()
Die Grundfläche ist ein Kreis, daher lautet die Formel
![]()
. Die Formel für das Volumen des Zylinders lautet daher:
![]()
Wir haben bereits die Funktion zur Optimierung. Aber es hängt von zwei Variablen ab (
![]()
Und
![]()
), während es nur von einem abhängen kann. Die Aussage sagt uns jedoch, dass die Fläche des Zylinders 54 cm 2 betragen muss, also werden wir diese Bedingung nutzen, um die Beziehung zwischen zu finden
![]()
Und
![]()
Um die Fläche eines Zylinders zu berechnen, müssen Sie seine Seitenfläche mit den Flächen der beiden Grundflächen addieren:
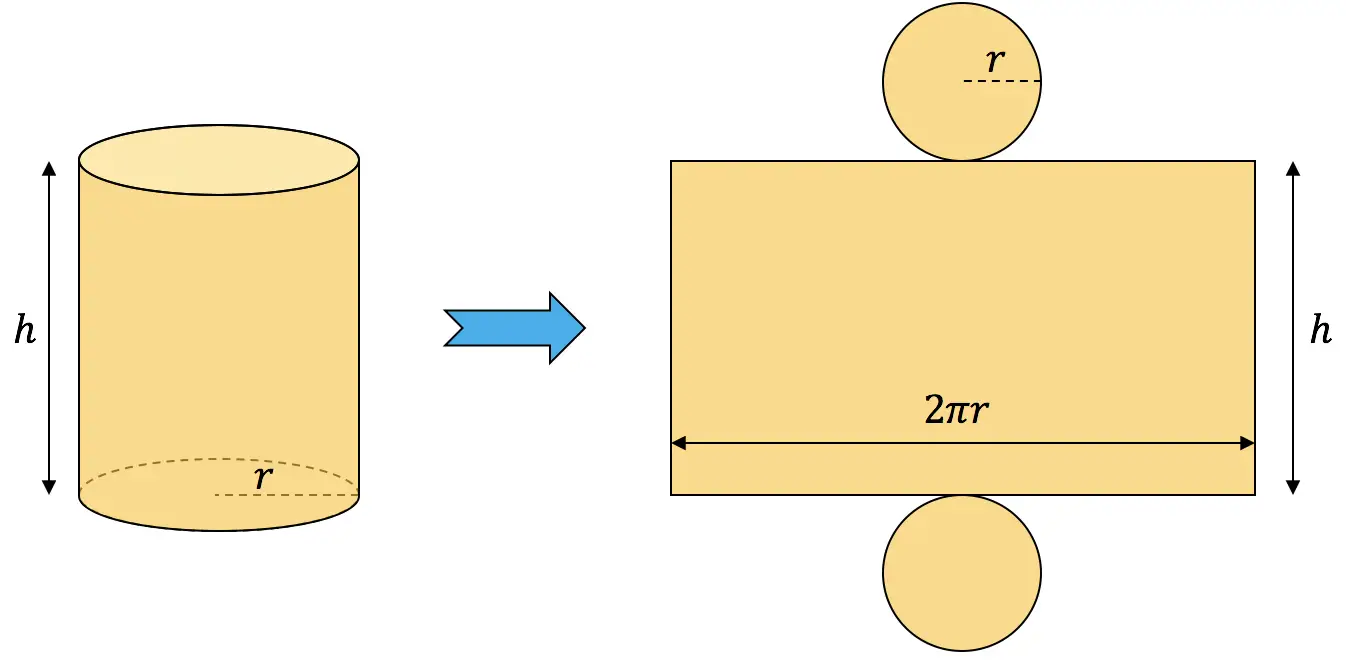
![]()
Die Fläche des Zylinders muss 54 cm 2 betragen, daher setzen wir den vorherigen Ausdruck auf 54, um die Beziehung zwischen zu erhalten
![]()
Und
![]()
![]()
Wir klären
![]()
![]()
![]()
Und wir ersetzen den Ausdruck, der in der zu optimierenden Funktion gefunden wird:
![]()
![]()
![]()
Schritt 2: Berechnen Sie die Ableitung der zu optimierenden Funktion.
![]()
Schritt 3: Finden Sie die kritischen Punkte.
Um die kritischen Punkte der Funktion zu finden, lösen wir
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Schritt 4: Untersuchen Sie die Monotonie der Funktion und bestimmen Sie das Maximum oder Minimum der Funktion.
Um die Monotonie der Funktion zu untersuchen, stellen wir den kritischen Punkt auf der Zahlengeraden dar:
Und jetzt bewerten wir das Vorzeichen der Ableitung in jedem Intervall, um herauszufinden, ob die Funktion zu- oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals den kritischen Punkt) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:
![]()
![]()
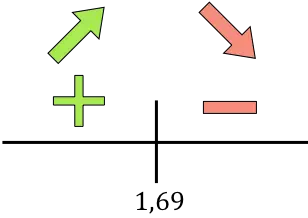
Wenn die Ableitung positiv ist, bedeutet dies, dass die Funktion zunimmt, und wenn die Ableitung negativ ist, bedeutet dies, dass die Funktion abnimmt. Daher sind die Wachstums- und Rückgangsintervalle:
Wachstum:
![]()
Verringern:
![]()
Die Funktion geht bei r=1,69 von ansteigend zu abnehmend über, sodass r=1,69 cm ein Maximum der Funktion ist .
Daher ist r=1,69 der Wert des Radius, der das maximale Volumen ergibt. Jetzt berechnen wir die Höhe:
![]()
Die Werte, die die maximale Lautstärke ergeben, sind also:
Radio
![]()
Höhe
![]()