Operationen mit Funktionen: Addition, Subtraktion, Produkt, Division und Zusammensetzung

In diesem Artikel erklären wir, welche Operationen mit Funktionen durchgeführt werden können. Sie können die Erklärung sowie gelöste Übungen zu Operationen mit Funktionen sehen. Und schließlich finden Sie die Eigenschaften der Operationen mit den Funktionen.

Was sind Operationen mit Funktionen?

Sie können 5 verschiedene Arten von Operationen mit Funktionen ausführen: Addition, Subtraktion, Produkt, Division und Zusammensetzung. Das heißt, zwei Funktionen können addiert, subtrahiert, multipliziert, dividiert oder zusammengesetzt werden.

Als nächstes werden wir sehen, wie jede Art von Operation mit ihren Funktionen und den jeweiligen Eigenschaften ausgeführt wird.

Summe der Funktionen

Der Wert der Summe (oder Addition) zweier Funktionen ist gleich der Summe der Werte jeder Funktion. Mit anderen Worten: Um das Bild einer Summenfunktion zu berechnen, addieren Sie einfach die Bilder der an der Operation beteiligten Funktionen.

$(f+g)(x)=f(x)+g(x)$

Darüber hinaus ist der Bereich der Summe zweier Funktionen der Schnittpunkt des Bereichs jeder summierten Funktion.

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)$

Sehen wir uns anhand eines Beispiels an, wie zwei Funktionen hinzugefügt werden:

$f(x)=x^2+1 \qquad g(x)=\log(x-1)$

Wir fügen zunächst die beiden Funktionen hinzu:

$(f+g)(x)=f(x)+g(x)=x^2+1+\log(x-1)$

Und jetzt finden wir den Definitionsbereich der Summenfunktion. Dazu berechnen wir den Definitionsbereich jeder Funktion separat:

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=(1,+\infty)$

➤ Siehe: So berechnen Sie den Definitionsbereich einer Funktion

Dann ist der Definitionsbereich der aus der Operation resultierenden Funktion:

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)=(1,+\infty)$

Jede Operation mit Funktionen muss von ihrer Domäne begleitet werden, um das Ergebnis vollständig zu definieren.

Subtraktion von Funktionen

Das Bild der Subtraktion (oder Differenz) zweier Funktionen ist die Subtraktion der Bilder jeder an der Operation beteiligten Funktion:

$(f-g)(x)=f(x)-g(x)$

Wie bei der Additionsfunktion entspricht der Subtraktionsbereich zweier Funktionen dem Schnittpunkt des Bereichs jeder Funktion.

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)$

Wenn also eine Funktion bei einem bestimmten Wert der unabhängigen Variablen x nicht definiert ist, ist auch die aus der Subtraktion resultierende Funktion nicht definiert.

Sehen wir uns anhand eines Beispiels an, wie zwei Funktionen subtrahiert werden:

$f(x)=\sqrt{x}\qquad g(x)=\cfrac{3}{x-4}$

Wir subtrahieren zunächst die beiden Funktionen:

$(f-g)(x)=f(x)-g(x)=\sqrt{x}-\cfrac{3}{x-4}$

Und dann bestimmen wir den Definitionsbereich der Subtraktionsfunktion:

$\text{Dom}(f)=[0,+\infty)\qquad\text{Dom}(g)=\mathbb{R}-\{4\}$

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)=[0,4)\cup (4,+\infty)$

Flaggschiffprodukt

Um das Produkt oder (die Multiplikation) zweier Funktionen zu berechnen, müssen Sie lediglich die Ausdrücke jeder Funktion multiplizieren.

$(f\cdot g)(x)=f(x)\cdot g(x)$

Andererseits ist der Definitionsbereich der Produktfunktion die Menge der Schnittpunkte des Definitionsbereichs jeder multiplizierten Funktion.

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)$

Wenn wir zum Beispiel die folgenden zwei Funktionen haben:

$f(x)=\sqrt[3]{x^2-1}\qquad g(x)=\cfrac{2}{3x+6}$

Zunächst führen wir die Bedienung des Produkts mit den beiden Funktionen durch:

$(f\cdot g)(x)=f(x)\cdot g(x)=\sqrt[3]{x^2-1}\cdot\cfrac{2}{3x+6}=\cfrac{2\sqrt[3]{x^2-1}}{3x+6}$

Und schließlich finden wir den Definitionsbereich der Funktion, die sich aus der Operation ergibt:

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}-\{-2\}$

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)=(-\infty,-2)\cup (-2,+\infty)$

Verteilung der Funktionen

Das numerische Ergebnis einer Division (oder eines Quotienten) zweier Funktionen entspricht der folgenden Gleichung:

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}$

Der Divisionsbereich zweier Funktionen ist jedoch die Menge der Schnittpunkte des Definitionsbereichs jeder Funktion abzüglich aller x, wodurch die Funktion, die als Teiler fungiert, aufgehoben wird, da wir sonst eine Unbestimmtheit erhalten würden.

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}$

Als Beispiel teilen wir die folgenden Funktionen auf:

$f(x)=5^x \qquad g(x)=x-3$

Die Funktionsverteilung ist wie folgt:

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\cfrac{5^x}{x-3}$

Andererseits besteht der Definitionsbereich jeder Funktion einzeln aus allen reellen Zahlen

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}$

Da es jedoch im Nenner eines Bruchs keine Null geben kann, müssen wir im Definitionsbereich der resultierenden Funktion alle Werte entfernen, die den Nenner aufheben (x=3).

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}=\mathbb{R}-\{3\}$

Zusammensetzung der Funktionen

Die Zusammensetzung von Funktionen ist die am schwierigsten zu lösende Operation, da es sich um das komplizierteste Konzept handelt.

Die Funktionskomposition besteht aus der aufeinanderfolgenden Anwendung zweier Funktionen. Algebraisch lässt sich die Zusammensetzung zweier Funktionen wie folgt ausdrücken:

$(g\circ f)(x)=g\Bigl(f(x)\Bigr)$

Andererseits der Bereich der Zusammensetzung von Funktionen

$(g\circ f)(x)$

ist äquivalent zur Menge aller Werte von x im Definitionsbereich der Funktion

$f$

wie zum Beispiel

$f(x)$

gehört zum Funktionsbereich

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Zum Beispiel angesichts der folgenden zwei Funktionen:

$f(x)=x^2+1 \qquad g(x)=3x-4$

Um die zusammengesetzte Funktion zu finden

$f$

gefolgt von

$g$

Wir müssen den Ausdruck von ersetzen

$f(x)$

wo es eins gibt

$x$

im Ausdruck von

$g(x):$

$\begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}$

In diesem Fall besteht der Definitionsbereich beider Funktionen vollständig aus reellen Zahlen, sodass auch der Definitionsbereich der zusammengesetzten Funktion aus reellen Zahlen besteht.

$\text{Dom}(g\circ f)=\mathbb{R}$

Wie Sie sehen, ist das Erstellen von Funktionen kein leicht zu verstehender Vorgang. Daher empfehlen wir Ihnen, die folgenden Funktionskompositionsübungen zu praktizieren:

➤ Siehe: gelöste Übungen zur Zusammensetzung von Funktionen

Eigenschaften von Operationen mit Funktionen

Von allen Operationen mit Funktionen zeichnen sich die Summe und das Produkt durch folgende Eigenschaften aus:

Assoziative Eigenschaft : Die Reihenfolge, in der 3 oder mehr Funktionen addiert oder multipliziert werden, ist irrelevant.

$f(x)+\bigl[g(x)+h(x)\bigr]=\bigl[f(x)+g(x)\bigr]+h(x)$

$f(x)\cdot \bigl[g(x)\cdot h(x)\bigr]=\bigl[f(x)\cdot g(x)\bigr] \cdot h(x)$

Kommutative Eigenschaft : Die Reihenfolge der Addition oder Multiplikation zweier Funktionen verändert das Ergebnis nicht.

$f(x)+g(x)=g(x)+f(x)$

$f(x)\cdot g(x)=g(x)\cdot f(x)$

Neutrales Element: Die Summenoperation und die Produktoperation haben konstante neutrale Elementfunktionen
$f(x)=0$

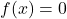
Und

$f(x)=1$

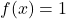
jeweils.

Symmetrisches Element : Die Summenfunktion hat die entgegengesetzte Funktion
$-f(x).$

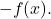
Verteilungseigenschaft : Diese Eigenschaft verknüpft die Summe und das Produkt von Operationen und basiert auf der folgenden Gleichheit:

$f(x)\cdot \bigl[g(x)+h(x)\bigr]=f(x)\cdot g(x)+f(x)\cdot h(x)$

Operationen mit funktionen: addition, subtraktion, produkt, division und zusammensetzung