Obere und untere Dreiecksmatrix

Auf dieser Seite sehen Sie, was eine Dreiecksmatrix ist und welche verschiedenen Arten von Dreiecksmatrizen es gibt, zusammen mit Beispielen. Darüber hinaus erfahren Sie, wie Sie die Determinante einer Dreiecksmatrix berechnen und welche Eigenschaften diese sehr interessante Matrix hat. Abschließend erklären wir auch, was eine Hessenberg-Matrix ist, da es sich um eine mit Dreiecksmatrizen verwandte Matrix handelt.

Was ist eine Dreiecksmatrix?

Definition der Dreiecksmatrix:

Eine Dreiecksmatrix ist eine quadratische Matrix, in der alle Elemente oberhalb oder unterhalb der Hauptdiagonale Null (0) sind.

Dreiecksmatrizen werden häufig in Berechnungen der linearen Algebra verwendet, da das Invertieren einer Dreiecksmatrix, die Berechnung ihrer Determinante oder sogar das Lösen linearer Gleichungssysteme mit dieser Art von Matrizen viel einfacher ist als mit Matrizen, die an allen Positionen andere Elemente als 0 haben. .

obere Dreiecksmatrix

Eine obere Dreiecksmatrix ist eine quadratische Matrix, deren Elemente unterhalb der Hauptdiagonale Null (0) sind.

Beispiel einer oberen Dreiecksmatrix:

untere Dreiecksmatrix

Eine untere Dreiecksmatrix ist eine quadratische Matrix, die in jedem Element, das über der Hauptdiagonale liegt, eine Null (0) hat.

Beispiel einer unteren Dreiecksmatrix:

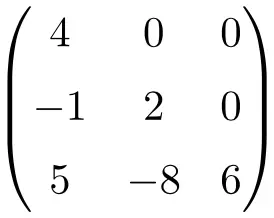
Manchmal werden diese Matrizen auch mit dem Buchstaben U für die obere Dreiecksmatrix und mit dem Buchstaben L für die untere Dreiecksmatrix bezeichnet. Obwohl diese Nomenklatur hauptsächlich im Englischen verwendet wird, steht das U tatsächlich für obere Dreiecksmatrix und das L für untere Dreiecksmatrix .

Beispiele für Dreiecksmatrizen

2 × 2-dimensionale Dreiecksmatrix

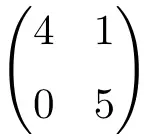
Beispiel einer oberen 2x2-Dreiecksmatrix

Dreiecksmatrix der Ordnung 3×3

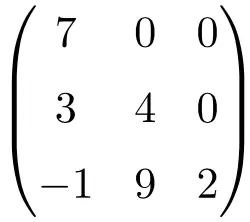
Beispiel einer unteren 3x3-Dreiecksmatrix

Dreiecksmatrix der Größe 4×4

Beispiel einer oberen 4x4-Dreiecksmatrix

Determinante einer Dreiecksmatrix

Die Determinante einer Dreiecksmatrix , egal ob obere oder untere Dreiecksmatrix, ist das Produkt der Elemente auf der Hauptdiagonale.

Schauen Sie sich die folgende Übung an, um herauszufinden, wie es ausreicht, die Multiplikation der Elemente der Hauptdiagonalen der Dreiecksmatrix zu berechnen, um ihre Determinante zu ermitteln:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Dieser Satz lässt sich leicht demonstrieren: Berechnen Sie einfach die Determinante einer Dreiecksmatrix anhand von Blöcken (oder Cofaktoren). Diese Demonstration wird unten anhand einer generischen Dreiecksmatrix detailliert beschrieben:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Andererseits wissen wir, dass eine Matrix invertierbar ist, wenn ihre Determinante von 0 verschieden ist. Wenn also kein Element auf der Hauptdiagonale 0 ist, ist auch die Dreiecksmatrix invertierbar und folglich regulär Matrix.

Eigenschaften der Dreiecksmatrix

Sehen wir uns nun die Eigenschaften von Dreiecksmatrizen an:

Das Produkt zweier oberer Dreiecksmatrizen ist gleich einer oberen Dreiecksmatrix. Und umgekehrt: Die Multiplikation zweier unterer Dreiecksmatrizen ergibt eine weitere untere Dreiecksmatrix.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

Die Transponierte einer oberen Dreiecksmatrix ist eine untere Dreiecksmatrix und umgekehrt: Die Transponierte einer unteren Dreiecksmatrix ist eine obere Dreiecksmatrix.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Eine Dreiecksmatrix ist invertierbar, wenn alle ihre Elemente auf der Hauptdiagonale ungleich Null sind, also von Null verschieden sind. In einem solchen Fall ist die Umkehrung einer oberen (unteren) Dreiecksmatrix auch eine obere (untere) Dreiecksmatrix.

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Darüber hinaus enthält die Hauptdiagonale der invertierten Matrix immer die Umkehrungen der Elemente der Hauptdiagonale der ursprünglichen Dreiecksmatrix.

Jede Diagonalmatrix ist sowohl eine obere Dreiecksmatrix als auch eine untere Dreiecksmatrix, zum Beispiel:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Eine Skalarmatrix ist also auch eine obere und untere Dreiecksmatrix. Zum Beispiel die Identitätsmatrix:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Offensichtlich ist die Nullmatrix auch eine obere und untere Dreiecksmatrix, da die Elemente oberhalb und unterhalb der Hauptdiagonale 0 sind:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Die Eigenwerte (oder Eigenwerte) einer Dreiecksmatrix sind die Elemente der Hauptdiagonale.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Eine obere oder untere Dreiecksmatrix ist immer in der Lage, auf der Basis von Eigenvektoren (oder Eigenvektoren) zu diagonalisieren .

Jede Matrix kann in das Produkt einer unteren Dreiecksmatrix und einer oberen Dreiecksmatrix faktorisiert werden . Das heißt, jede Matrix kann in eine Dreiecksmatrixmultiplikation umgewandelt werden. Wenn die Matrix außerdem invertierbar ist, ist diese Transformation eindeutig. Um eine Matrix zu faktorisieren, wird häufig die LU-Zerlegungsmethode verwendet.

Triangularisieren Sie eine Matrix

Es gibt mehrere Sätze über Matrizen, die durch Ändern der Basis triangularisiert werden können. Hier werden wir jedoch sehen, wie man eine Matrix trianguliert, indem man elementare Transformationen auf die Linien anwendet, wie bei der Gauß-Methode.

Zum Beispiel:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

Und auf diese Weise haben wir die ursprüngliche Matrix bereits triangularisiert.

Denken Sie daran, dass die elementaren Transformationen zwischen Linien in der Gaußschen Methode zulässig sind:

Ersetzen Sie eine Linie durch die lineare Kombination anderer Linien.
Multiplizieren oder dividieren Sie alle Terme in einer Zeile mit einer Zahl ungleich 0.
Bestellzeilen bearbeiten.

Hessenberg-Matrix

Die Definition der Hessenberg-Matrix lautet wie folgt:

Die Hessenberg-Matrix ist eine „fast“ dreieckige Matrix, das heißt, dass alle ihre Elemente ab der ersten Subdiagonalen (obere Hessenberg-Matrix) oder der ersten Superdiagonalen (untere Hessenberg-Matrix) Null sind.

Ich bin sicher, dass man es am besten anhand eines Beispiels einer oberen Hessenberg-Matrix und eines weiteren Beispiels einer unteren Hessenberg-Matrix verstehen kann:

Obere Hessenberg-Matrix

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Untere Hessenberg-Matrix

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Eine Matrix, die sowohl eine obere als auch eine untere Hessenberg-Matrix ist, ist eine tridiagonale Matrix .

Diese Matrix ist nach Karl Hessenberg benannt, einem bekannten deutschen Ingenieur und Mathematiker des 20. Jahrhunderts.

Schließlich weist dieser Matrixtyp die Besonderheit auf, dass bei Multiplikation mit einer Dreiecksmatrix immer eine Hessenberg-Matrix entsteht.

Obere und untere dreiecksmatrix