Auf dieser Seite finden Sie die Erklärung der Nullmatrix, auch Nullmatrix genannt. Anhand von Beispielen werden Sie auch sehen, dass die Werte ihrer Elemente unabhängig von der Dimension der Matrix sind, und schließlich finden Sie alle Eigenschaften dieses Matrixtyps.
Was ist die Nullmatrix?
Die Nullmatrix (oder Nullmatrix) ist eine Matrix, deren Elemente alle gleich Null (0) sind.
Daher kann diese Matrix nach der Definition einer Nullmatrix alle möglichen Dimensionen haben, solange alle ihre Zahlen Null sind. Schauen Sie sich die folgenden Beispiele an:
Beispiele für Nullmatrizen
Beispiel einer 2 × 2-Nullmatrix
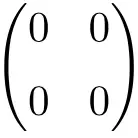
Beispiel einer 3 × 3-Nullmatrix
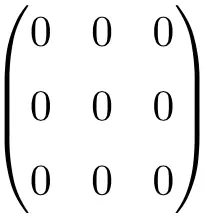
Beispiel einer 4 × 4-Nullmatrix
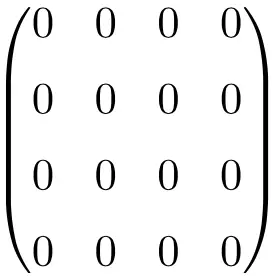
Es mag Ihnen jetzt so vorkommen, als ob diese ganz spezielle Matrix keine Rolle spielt, da es sich lediglich um eine Matrix voller Nullen handelt. In der Mathematik, insbesondere im Bereich der linearen Algebra, ist sie jedoch eine sehr nützliche Matrix, da sie Berechnungen erheblich vereinfacht.
Eigenschaften der Nullmatrix
Null- (oder Null-)Matrizen haben die folgenden Eigenschaften:
- Die Nullmatrix ist das neutrale Element der Matrixadditionsoperation, daher:
![]()
- Die Matrixmultiplikation hat die multiplikative Eigenschaft Null, d. h. das Produkt einer beliebigen Matrix multipliziert mit der Nullmatrix ist gleich 0.
![]()
- Wenn die Matrix quadratisch ist, ist die Nullmatrix sowohl symmetrisch als auch antisymmetrisch .
- Die Nullmatrix ist die einzige Matrix, deren Rang Null ist.
- Die Determinante der Nullmatrix ergibt immer 0, daher hat dieser Matrixtyp keine Umkehrung (es handelt sich um eine singuläre Matrix).
- Offensichtlich ist die Nullmatrix ein Beispiel für eine nilpotente Matrix .