▷ Lösen Sie die Nullunbestimmtheit zwischen Null (0/0)

In diesem Artikel erklären wir, wie man den Grenzwert einer Funktion speichert, wenn sie eine Unsicherheit von 0/0 ergibt. Darüber hinaus können Sie anhand gelöster Aufgaben die Unbestimmtheit von Null zwischen Null üben.

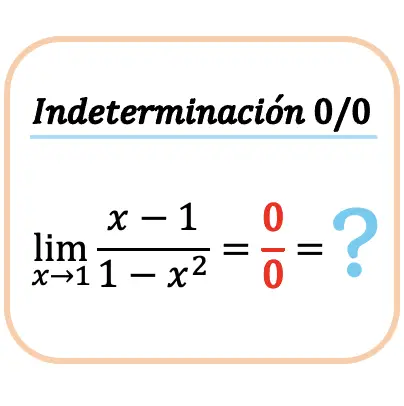
So lösen Sie die Nullunbestimmtheit zwischen Null (0/0)

Wir werden dann sehen, wie man den Grenzwert einer Funktion berechnet, wenn sie eine Nullunbestimmtheit zwischen Null (0/0) ergibt. Dazu berechnen wir Schritt für Schritt ein Beispiel:

$\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}$

Wir versuchen zunächst, den Grenzwert zu berechnen, indem wir den Wert von x in die Funktion einsetzen:

$\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}$

Aber wir erhalten die Unbestimmtheit 0 dividiert durch 0.

Wenn der Grenzwert einer Punktfunktion die Unsicherheit 0/0 ergibt, ist es notwendig, die Polynome des Zählers und des Nenners zu faktorisieren und dann die gemeinsamen Faktoren zu vereinfachen.

Wir müssen daher die Polynome des Zählers und Nenners des Bruchs faktorisieren. Dazu verwenden wir die Ruffini-Regel:

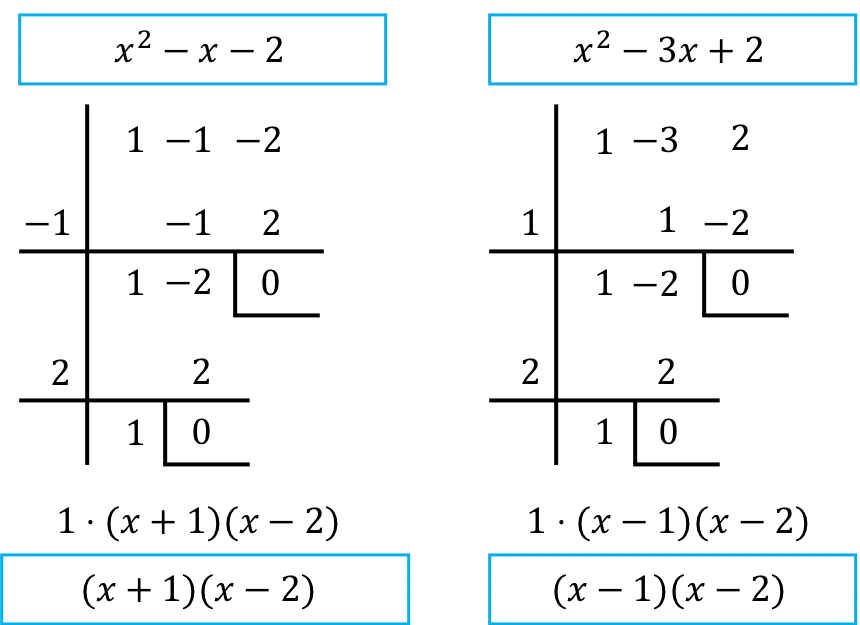
➤ Wenn Sie nicht wissen , wie man ein Polynom faktorisiert , empfehlen wir Ihnen, die Erklärung auf unserer auf Polynome spezialisierten Website zu lesen: www.polinomios.org

Sobald die Polynome faktorisiert sind, ist der Grenzwert wie folgt:

$\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}$

Wir können den Grenzwert nun vereinfachen, indem wir die Faktoren eliminieren, die sich im Zähler und Nenner des Bruchs wiederholen:

$\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}$

Und schließlich berechnen wir den Grenzwert neu:

$\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}$

Wie Sie sehen, ist es sehr einfach, die Lösung im Limes zu finden, sobald wir die Polynome faktorisieren und vereinfachen.

Unbestimmtheit 0/0 mit Wurzeln

Wir haben gerade gesehen, wie die 0/0-Unbestimmtheiten rationaler Funktionen aufgelöst werden. Wenn der Grenzwert jedoch eine irrationale (oder radikale) Funktion ist, wird die 0/0-Unbestimmtheit anders aufgelöst.

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}$

Zunächst versuchen wir, das Limit aufzulösen, indem wir die folgenden Vorgänge ausführen:

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}$

Aber wir erhalten eine Null-über-Null-Unbestimmtheit.

Wenn der Grenzwert einer Funktion mit Wurzeln die Unbestimmtheit 0/0 ergibt , müssen Sie Zähler und Nenner des Bruchs mit dem Konjugat des Wurzelausdrucks multiplizieren.

➤ Denken Sie daran, dass das Konjugat derselbe irrationale Ausdruck ist, jedoch mit geändertem Mittelzeichen.

Als nächstes multiplizieren wir sowohl den Zähler als auch den Nenner des Bruchs mit dem Konjugat des Wurzelausdrucks:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}$

Innerhalb dieser Art von Grenzen erhalten wir durch diesen Schritt immer eine bemerkenswerte Identität, die wir vereinfachen können. In diesem Fall haben wir im Nenner das Produkt aus einer Summe und einer Differenz, also:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}$

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}$

Wir vereinfachen den Faktor, der sich im Zähler und Nenner wiederholt:

$\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)$

Und auf diese Weise können wir das Ergebnis des Grenzwerts finden:

$\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2$

Gelöste Übungen zur Unbestimmtheit 0/0

Nachfolgend haben wir mehrere Schritt-für-Schritt-Übungen zu den Grenzen von Funktionen vorbereitet, die 0/0-Unbestimmtheiten ergeben. Sie können es versuchen und dann die Lösung prüfen.

Vergessen Sie nicht, dass Sie uns in den Kommentaren alle Fragen zur Lösung von Limits stellen können!

Übung 1

Berechnen Sie den Grenzwert der folgenden rationalen Funktion am Punkt x=-2.

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

Sehen Sie sich die Lösung an

Logischerweise versuchen wir zunächst, das Limit zu lösen:

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

Am Ende haben wir jedoch eine 0/0-Unbestimmtheit. Wir müssen daher die Polynome des Zählers und des Nenners faktorisieren:

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

Jetzt vereinfachen wir den Bruch, indem wir die Klammern entfernen, die sich im Zähler und Nenner wiederholen:

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

Und schließlich berechnen wir den Grenzwert mit dem vereinfachten Bruch neu:

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

Übung 2

Lösen Sie den Grenzwert der folgenden Funktion, wenn x sich -1 nähert:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

Sehen Sie sich die Lösung an

Wir versuchen zunächst wie gewohnt, das Limit aufzulösen:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

Aber wir erhalten die Unbestimmtheit 0 zwischen 0. Wir müssen also die 2 Polynome des Bruchs faktorisieren:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

Wir können nun die Polynome vereinfachen:

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

Und wir lösen das Limit:

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

Übung 3

Bestimmen Sie die Lösung des Grenzwertes der folgenden Radikalfunktion:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

Sehen Sie sich die Lösung an

Zuerst prüfen wir, ob der Grenzwert eine Art Unbestimmtheit ergibt:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

Der Grenzwert ergibt die Unbestimmtheit Null dividiert durch Null und wir haben eine Wurzel in der Funktion. Wir müssen daher Zähler und Nenner des Bruchs mit dem Konjugat des Wurzelausdrucks multiplizieren:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

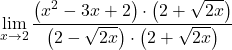
Der Nenner entspricht der Entwicklung der bemerkenswerten Identität des Produkts aus einer Summe und einer Differenz. Wir können ihn daher vereinfachen:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

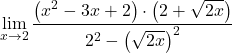
Allerdings können wir die Terme des Bruchs noch nicht vereinfachen. Wir müssen daher die Polynome faktorisieren:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

Auf diese Weise können wir den Bruch vereinfachen:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

Und jetzt können wir das Ergebnis des Grenzwerts ermitteln:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

Übung 4

Berechnen Sie den Grenzwert, wenn x sich 0 der folgenden Wurzelfunktion nähert:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

Sehen Sie sich die Lösung an

Zuerst versuchen wir, wie immer, den Grenzwert der Funktion zu berechnen:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

Aber wir erhalten die unbestimmte Form von 0/0. Daher multiplizieren wir Zähler und Nenner der Funktion mit dem Konjugat des irrationalen Ausdrucks:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

Wir wenden die entsprechende Notable-Identity-Formel an, um den Nenner zu vereinfachen:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

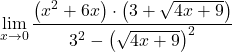
Jetzt faktorisieren wir das Binomial des Zählers, indem wir den gemeinsamen Faktor bilden:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

Wir vereinfachen die Faktoren, die sich im Zähler und Nenner der Funktion wiederholen:

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

Und schließlich lösen wir den Grenzwert der Funktion:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

Übung 5

Lösen Sie den folgenden Grenzwert mit der 0/0-Unbestimmtheitsmethode:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

➤ Siehe: So berechnen Sie die seitlichen Grenzen einer Funktion

Sehen Sie sich die Lösung an

Wir versuchen zunächst, das Limit aufzulösen:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

Aber im Limes erhalten wir eine Null-gegen-Null-Unbestimmtheit. Deshalb faktorisieren wir die Polynome von Zähler und Nenner:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

Jetzt vereinfachen wir den Bruch, indem wir die Faktoren eliminieren, die sich im Zähler und Nenner wiederholen:

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

Und wir berechnen den Grenzwert noch einmal:

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

Aber jetzt haben wir es mit der Unbestimmtheit einer durch 0 dividierten Zahl zu tun. Wir müssen daher die seitlichen Grenzen der Funktion berechnen, wenn x gegen -1 tendiert.

Wir lösen zunächst nach dem seitlichen Grenzwert der Funktion am Punkt x=-1 auf der linken Seite:

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

Und dann berechnen wir die seitliche Grenze der Funktion am Punkt x=-1 rechts:

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

Da die beiden seitlichen Grenzen nicht zusammenfallen, existiert der Grenzwert der Funktion bei x=-1 nicht:

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

Nullunbestimmtheit zwischen null (0/0)

So lösen Sie die Nullunbestimmtheit zwischen Null (0/0)

Unbestimmtheit 0/0 mit Wurzeln

Gelöste Übungen zur Unbestimmtheit 0/0

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Kommentar verfassen Kommentieren abbrechen