Regelmäßige matrix

Auf dieser Seite sehen Sie, was eine Normalmatrix ist, sowie Beispiele für Normalmatrizen. Darüber hinaus finden Sie die Eigenschaften dieser Art von Matrizen und Übungen Schritt für Schritt gelöst.

Was ist eine Normalmatrix?

Die normale Array-Definition lautet:

Eine normale Matrix ist eine komplexe Matrix, die multipliziert mit ihrer konjugierten Transponiertenmatrix gleich dem Produkt der konjugierten Transponierten mit sich selbst ist.

A\cdot A^*=A^*\cdot A

Gold

A^*

ist die konjugierte Transponierungsmatrix von

A

.

Wenn es sich jedoch um reelle Zahlenmatrizen handelt, läuft die vorherige Bedingung darauf hinaus, dass eine Matrix mit ihrer Transponierten kommutiert, das heißt:

A\cdot A^t=A^t\cdot A

Denn offensichtlich ist die konjugierte Transpositionsmatrix einer realen Matrix einfach die Transpositionsmatrix (oder Transpositionsmatrix).

Beispiele für Normalmatrizen

Beispiel mit komplexen Zahlen

Die folgende komplexe quadratische Matrix der Dimension 2×2 ist normal:

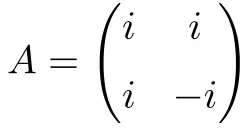
Beispiel einer normalen Matrix mit komplexen Zahlen der Dimension 2x2

Die Demonstration seiner Normalität ist unten beigefügt:

\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}

\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}

Beispiel mit reellen Zahlen

Die folgende quadratische Matrix mit reellen Zahlen der Ordnung 2 ist ebenfalls normal:

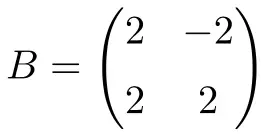
Beispiel einer normalen Matrix mit reellen Zahlen der Dimension 2x2

Da es in diesem Fall nur reelle Zahlen gibt, reicht es zum Beweis, dass es normal ist, zu überprüfen, ob die Matrix mit ihrer Transponierten vertauschbar ist:

\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}

\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}

Eigenschaften normaler Matrizen

Normale Matrizen haben die folgenden Eigenschaften:

  • Alle Normalmatrizen sind diagonalisierbare Matrizen.
  • Ebenso ist eine antihermitesche Matrix eine Normalmatrix.
  • Wenn A eine Normalmatrix ist, sind die Eigenwerte (oder Eigenwerte) der konjugierten transponierten Matrix A* die konjugierten Eigenwerte von A.

\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i

\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i

  • In normalen Matrizen sind die den verschiedenen Eigenwerten zugeordneten Eigenvektoren (oder Eigenvektoren) orthogonal.
  • Besteht eine Matrix nur aus reellen Zahlen und ist symmetrisch , handelt es sich gleichzeitig um eine Normalmatrix.
  • Schließlich ist jede aus reellen Zahlen gebildete orthogonale Matrix auch eine Normalmatrix.

Gelöste Übungen für normale Matrizen

Übung 1

Stellen Sie sicher, dass die folgende komplexe Matrix der Dimension 2 × 2 normal ist:

\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}

Um zu zeigen, dass die Matrix normal ist, müssen wir zunächst ihre konjugierte Transponierte berechnen:

\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}

Und jetzt führen wir die Verifizierung durch, indem wir die Matrix A mit der Matrix A* in beide möglichen Richtungen multiplizieren:

\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}

\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}

Das Ergebnis beider Multiplikationen ist das gleiche, daher ist Matrix A normal.

Übung 2

Zeigen Sie, dass die folgende reelle Matrix der Größe 2 × 2 normal ist:

\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}

Da es sich in diesem Fall um eine Umgebung mit ausschließlich reellen Zahlen handelt, genügt es zu überprüfen, ob das Matrixprodukt zwischen der Matrix A und ihrer Transponierten unabhängig von der Richtung der Multiplikation das gleiche Ergebnis liefert:

\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}

\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}

Das Ergebnis beider Produkte ist das gleiche, daher ist Matrix A normal.

Übung 3

Bestimmen Sie, ob die folgende Matrix komplexer Zahlen der Ordnung 2 normal ist:

\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}

Um zu überprüfen, ob die Matrix normal ist, müssen wir zunächst ihre konjugierte Transponierte berechnen:

\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}

Und jetzt prüfen wir, ob die Matrix A und ihre konjugierte Transponierte umschaltbar sind:

\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}

\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}

Das Ergebnis beider Multiplikationen ist das gleiche, daher ist Matrix A normal.

Übung 4

Stellen Sie sicher, dass die folgende reelle Matrix der Dimension 3×3 normal ist:

\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}

Da die Matrix vollständig aus reellen Elementen besteht, genügt es zu überprüfen, dass das Matrixprodukt zwischen der Matrix A und ihrer Transponierten unabhängig von der Richtung der Multiplikation ist:

\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}

\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}

Das Ergebnis beider Produkte ist das gleiche, daher ist Matrix A normal.

Übung 5

Bestimmen Sie, ob die folgende komplexe Matrix der Ordnung 3×3 normal ist:

\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}

Zuerst berechnen wir die konjugierte Transponierte der Matrix:

\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}

Jetzt müssen wir die Matrixmultiplikationen zwischen der Matrix A und ihrer konjugierten Transponierten in beide möglichen Richtungen durchführen. Allerdings ist die konjugierte Transponierungsmatrix von A gleich der Matrix A selbst, es handelt sich also um eine hermitesche Matrix. Aus den Eigenschaften normaler Matrizen folgt daher, dass A eine normale Matrix ist , da jede hermitesche Matrix eine normale Matrix ist.

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen