Das Newtonsche Binomial ist eine mathematische Formel, die verwendet wird, um die Summe zweier Terme auszudrücken, die mit einer bestimmten Potenz multipliziert werden . Diese nach dem britischen Mathematiker Isaac Newton benannte Formel wird in vielen Bereichen der Mathematik verwendet.
Es ist beispielsweise in der Statistik, der Wahrscheinlichkeitstheorie sowie der Differential- und Integralrechnung nützlich. Mit dem Binomialsatz können wir auf einfache Weise die Potenz eines Binomials berechnen.
Einfach ausgedrückt basiert Newtons Binomial auf einer Formel, mit der jeder algebraische Ausdruck der Form (a+b) n gelöst werden kann. Obwohl diese Formel nach Isaac Newton benannt ist, ist es erwähnenswert, dass es Kontroversen über ihren Ursprung gibt.
Das heißt, einige Untersuchungen deuten darauf hin, dass der Binomialsatz im Nahen Osten Anwendung findet.
Wann wurde Newtons Binomial entwickelt?
Newtons Binomialsatz, auch bekannt als Newtons Binomialsatz, wurde 1665 entwickelt und erstmals 1676 in zwei Briefen des Beamten der Royal Society mitgeteilt .
Diese Briefe waren eine Antwort an den deutschen Mathematiker Gottfried Wilhelm von Leibniz, der mathematische Untersuchungen unendlicher Reihen besser verstehen wollte. Newton teilte die Ergebnisse seines Theorems mit und Leibniz erkannte, dass es sich um eine nützliche Technik handelte, um Ergebnisse in Quadraturen oder Reihen zu erhalten.
Diese Beobachtung ließ Newton zu dem Schluss kommen, dass es möglich sei , mit unendlichen Reihen auf die gleiche Weise zu operieren wie mit endlichen Polynomausdrücken . Obwohl Newton seinen Satz nie veröffentlichte, veröffentlichte ihn der britische Mathematiker John Wallis 1685 in seiner Algebra und schrieb seine Entstehung Newton zu.
Warum heißt es Newtons Binomial?
Das Newtonsche Binomial ist nach dem englischen Mathematiker und Physiker Isaac Newton benannt, der es im 17. Jahrhundert entwickelte . Newton war nicht der Erste, der diesen Satz entdeckte, aber er war der Erste, der seine Gültigkeit für jede positive ganze Zahl n bewies.
Das Newtonsche Binomial ist ein sehr nützliches mathematisches Werkzeug in der Algebra und Analysis und wird häufig in Bereichen wie Physik, Statistik, Ingenieurwesen und Informatik verwendet.
Was ist Newtons Binomialformel?
Wie wir bereits erwähnt haben, ist Newtons Binomial die Formel, mit der die Potenzen eines Binomials ermittelt werden können . Um diese Binomialstärke zu ermitteln, werden „Binomialkoeffizienten“ verwendet. Der vorherige Begriff bezieht sich auf Sequenzen von Kombinationen.
Vor diesem Hintergrund können wir Newtons Binomialformeln wie folgt aufschlüsseln:
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (a + b) 3 = a 3 + 3a 2 b + 3 ab 2 + b 3
Die mathematischen Ausdrücke, die sich auf die Entwicklung von (a+b) n beziehen, werden als bemerkenswerte Einheiten bezeichnet und ermöglichen es, eine allgemeine Formel zu erhalten, die diese Operation für jede natürliche Zahl „n“ darstellt.
Indem wir die Koeffizienten jedes resultierenden Polynoms untersuchen, können wir eine Folge erkennen, die dem sogenannten Pascal-Dreieck folgt.
Die Folge des Pascalschen Dreiecks beginnt mit der Zahl 1, und in jeder folgenden Zeile sind die letzten Ziffern immer 1. Zwischenwerte erhält man durch Addition der beiden Zahlen aus der vorherigen Zeile, die direkt über dem zu berechnenden Wert stehen.
Wie findet man einen Begriff im Newtonschen Binomial?
Um einen bestimmten Begriff im Newtonschen Binomial zu finden, wird die allgemeine Formel verwendet:
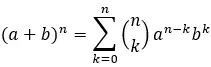
Gold:
a und b sind die Koeffizienten des Binomials.
n ist der Exponent des Binomials.
k ist der spezifische Begriff, den wir finden möchten.
Σ stellt die Summe von k=0 bis n dar.
[nk] ist der Binomialkoeffizient, der nach der folgenden Formel berechnet wird:
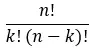
Daher lautet die vollständig erweiterte Formel:
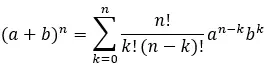
Beispiel eines gelösten Newton-Binoms
Sobald diese Werte gefunden sind, werden sie in die Formel eingesetzt und der Ausdruck wird aufgelöst, um den spezifischen Term zu erhalten. Wenn wir beispielsweise den fünften Term des Binomials (2x + 3) 6 finden wollten, hätten wir:
eins = 2x
b = 3
n=6
k = 5
Also, mit der Formel:
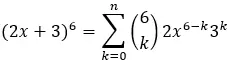
Der fünfte Term entspricht k=5, wir haben also:
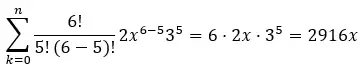
Daher ist der fünfte Term des Binomials (2x + 3) 6 2916x.
Was ist ein Newton-Binom vom Grad 5?
Ein Newton-Binom vom Grad 5 ist ein algebraischer Ausdruck der Form (a + b) 5 , wobei „a“ und „b“ Variablen sind und der Exponent 5 den Grad des Binomials angibt . Wenn wir diesen Ausdruck erweitern, erhalten wir ein quadratisches Polynom mit sechs Termen:
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Jeder Term dieses Polynoms wird durch Kombination der Koeffizienten des Binomials mit den Potenzen „a“ und „b“ erhalten. Beispielsweise erhält man den zweiten Term (5a 4 b), indem man den Binomialkoeffizienten (5 wähle 1 = 5) mit „a“ in der vierten Potenz und mit b in der ersten Potenz multipliziert.
Newtons Binome vom Grad 5 sind in verschiedenen Bereichen der Mathematik und Physik nützlich, beispielsweise in der Statistik, der Wahrscheinlichkeitstheorie und der Quantenmechanik.
Welche Anwendungen gibt es mit dem Newtonschen Binomial?
Das Newtonsche Binomial hat eine Vielzahl von Anwendungen in verschiedenen Bereichen, darunter:
- Berechnung von Wahrscheinlichkeiten : Der Binomialsatz wird verwendet, um die Wahrscheinlichkeiten von Binomialereignissen zu berechnen , beispielsweise dem Münzwurf oder dem Erfolg oder Misserfolg einer Reihe von Tests.
- Zahlentheorie – Newtons Binomial wird verwendet, um Polynome zu erweitern und Gleichungen in der Zahlentheorie zu vereinfachen.
- Statistik : Newtons Binomial wird zur Berechnung von Binomialverteilungen und zur Konstruktion von Konfidenzintervallen verwendet.
- Physik – In der Physik wird der Binomialsatz unter anderem in der Relativitätstheorie und der Quantenmechanik verwendet.
- Wirtschaft und Finanzen : Das Newtonsche Binomial wird zur Berechnung des aktuellen und zukünftigen Werts von Cashflows im Zeitverlauf und bei der Bewertung von Finanzoptionen verwendet.
- Programmierung und Informatik : Newtons Binomial wird in der Algorithmenentwicklung und Computerprogrammierung verwendet.
Warum ist Newtons Binomial wichtig?
Das Newtonsche Binomial ist relevant, weil es ein grundlegendes mathematisches Werkzeug für die Entwicklung der Algebra und der Zahlentheorie ist. Damit können Sie das Ergebnis der Quadrierung oder eine andere Potenz eines Binomials berechnen, was sehr nützlich ist, um Gleichungen zu lösen und algebraische Ausdrücke zu vereinfachen.
Darüber hinaus findet es unter anderem Anwendungsmöglichkeiten in Bereichen wie Statistik, Wahrscheinlichkeitsrechnung und Physik . Zusammenfassend lässt sich sagen, dass das Newtonsche Binomial ein wesentliches Konzept in der Mathematik ist und sein Verständnis für den Fortschritt in vielen Studienbereichen von entscheidender Bedeutung ist.
Gibt es andere Möglichkeiten, Newtons Binomial auszudrücken?
Ja, es gibt andere Möglichkeiten, Newtons Binomial auszudrücken. Beispielsweise kann es mithilfe der kombinatorischen Notation durch Binomialkoeffizienten ausgedrückt werden.
Darüber hinaus kann es mithilfe der Euler-Formel in Form von Exponentialfunktionen und trigonometrischen Funktionen ausgedrückt werden. Ebenso in Bezug auf die Gammafunktion unter Verwendung der Legendre-Formel. Diese alternativen Ausdrücke können in verschiedenen Kontexten und mathematischen Problemen nützlich sein.
Beispiele für Newton-Binomiale
Sehen wir uns dann einige einfache Beispiele für die Anwendung des Newtonschen Binomials an.
Beispiel 1: Berechnen Sie den Term der Ordnung 3 in der Entwicklung von (x + y) 5 .
Lösung: Bei der Entwicklung von (x + y) 5 beträgt der Koeffizient des ersten Termes 1, der Koeffizient des zweiten Termes 5, der Koeffizient des dritten Termes 10 und der Koeffizient des vierten Termes 10 Der Koeffizient des fünften Termes ist 5 und der Koeffizient des sechsten Termes ist 1.
Die Laufzeit der Anordnung 3 lautet daher:
10x 2 und 3
Beispiel 2: Finden Sie den unabhängigen Term in der Entwicklung von (2x – 1) 4 .
Lösung: In der Entwicklung von (2x – 1) 4 findet sich der unabhängige Term in der Kombination (2x) p (-1) (4-p) , wobei p der Wert ist, der den Exponenten von (2x) p und bildet (-1) (4-p) addieren sich zu 4.
Der unabhängige Begriff lautet daher:
(2x) 2 (-1) 2 = 4
Beispiel 3: Finden Sie den Term höchsten Grades in der Entwicklung von (3x – 2y) 6 .
Lösung: Der Term höchster Ordnung in der Entwicklung von (3x – 2y) 6 findet sich in der Kombination (3x) p (-2y) (6-p) , wobei p der Wert ist, der den Exponenten von (3x) p und bildet (-2y) (6-p) entspricht dem Grad des Binomials, der 6 ist.
Daher lautet der höchste Gradbegriff:
(3x) 3 (-2y) 3 = -216x 3 und 3