Seit der Antike ist die Menge der natürlichen Zahlen die Grundlage, auf der viele Zweige der Mathematik aufgebaut sind. Auf diesen Zahlen basieren beispielsweise Arithmetik und Geometrie. Aus diesem Grund werden wir in diesem kurzen Artikel die Definition natürlicher Zahlen und alle mit dieser Menge verbundenen Konzepte sehen.
Was sind die natürlichen Zahlen?
Natürliche Zahlen sind eine Reihe abstrakter Elemente, die wir zum Zählen und Ordnen von Objekten in der physischen Welt verwenden. In der Mathematik wird die Menge der natürlichen Zahlen im Allgemeinen durch den Buchstaben ℕ dargestellt. Diese setzt sich aus allen positiven ganzen Zahlen ohne Dezimalzahl zusammen, die keine Brüche sind: ℕ = {1, 2, 3, 4, 5, 6…}.
Mit anderen Worten: Natürliche Zahlen sind alle positiven ganzen Zahlen , die zum Zählen realer Objekte verwendet werden können. Auf diese Weise können wir sagen, dass die Zahl 1 eine natürliche Zahl ist, weil wir sie zum Zählen realer Objekte verwenden können. Wir können zum Beispiel einen Apfel und zwei Birnen haben, was insgesamt drei Früchte ergeben würde.
Im folgenden Bild zeigen wir Ihnen ein Diagramm, das alle Zahlenmengen zusammenfasst, sodass Sie sehen können, wo sich die Menge ℕ befindet. Und welche Beziehung hat sie zu den anderen, um den Begriff der natürlichen Zahl besser zu verstehen? Bevor Sie mit der Erklärung fortfahren, empfehlen wir Ihnen, einen genauen Blick auf die Concept Map zu werfen und zu versuchen, sie zu verstehen.

Wie erkennt man, ob eine Zahl natürlich ist oder nicht?
Wie wir bereits gesagt haben, sind die natürlichen Zahlen diejenigen, die wir zum Zählen und Ordnen verwenden. Um zu wissen, ob ein Wert natürlich ist oder nicht, müssen wir Folgendes beachten: Eine Zahl ℕ hat kein negatives Vorzeichen, sie hat keine Dezimalstellen, sie hat keine imaginäre Einheit und sie ist kein Bruch. Als nächstes zeigen wir Ihnen eine Liste der ersten 100 natürlichen Zahlen:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 6 4, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75 , 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 und 100 .
Wie werden natürliche Zahlen gelesen und geschrieben?
Die natürlichen Zahlen folgen dem dezimalen Zahlensystem , das heißt, die Werte haben die Zahl Zehn als arithmetische Basis. Alle Zahlen bestehen aus mindestens einer dieser neun Ziffern: 1, 2, 3, 4, 5, 6, 7, 8 und 9. Und denken Sie daran, dass eine natürliche Zahl auf keinen Fall einen Dezimalpunkt oder ein negatives Vorzeichen hat .
Bei allen arithmetischen Operationen werden diese Zahlen nach der mathematischen Notation geschrieben. Wenn Sie Zweifel an einem Symbol oder Ausdruck haben, empfehlen wir Ihnen, auf diesen letzten Link zuzugreifen und den Artikel zu lesen. Dort finden Sie alle Informationen zur mathematischen Sprache und alle Notationen.
Eigenschaften natürlicher Zahlen
Einige der wichtigsten Merkmale natürlicher Zahlen sind:
- Die erste natürliche Zahl ist 1, da 0 keine natürliche Zahl ist.
- Sie dienen zum Messen, Kontrollieren und Berechnen: Mit ihnen können Längen, Gewichte, Kapazitäten usw. gemessen werden.
- Sie können miteinander verglichen werden: Wir können sagen, welche größer oder kleiner als eine andere natürliche Zahl ist.
- Sie haben eine Reihenfolge: Natürliche Zahlen folgen einer logischen Reihenfolge, beginnend bei 1 und endend bei Unendlich.
- Zwei Naturmenschen können weder denselben Nachfolger noch denselben Vorgänger haben.
- Alle natürlichen Zahlen sind ganze Zahlen, da natürliche Zahlen positive ganze Zahlen sind, keine Dezimalzahlen oder Brüche.
Zum Abschluss dieses Abschnitts hinterlassen wir Ihnen eine Reihe von Klarstellungen zu dieser Menge, die bei Schülern oft Zweifel aufkommen lassen: Die Zahl Null ist keine natürliche Zahl, natürliche Zahlen sind ganze Zahlen, natürliche Zahlen können keine negativen Zahlen sein, natürliche Zahlen haben keine Dezimalzahl Orte und natürliche Zahlen sind unendlich.
Darstellung natürlicher Zahlen
Die Menge der natürlichen Zahlen , auch ℕ genannt, besteht aus den positiven ganzen Zahlen: 1, 2, 3, 4… und so weiter. Diese Menge wird durch die folgende Notation dargestellt: ℕ = {1, 2, 3, 4, 5…}. Man kann sie aber auch anschaulicher darstellen, indem man sie auf dem Zahlenstrahl platziert.
Bei dieser zweiten Methode wird eine gerade horizontale Linie gezeichnet und die Werte der natürlichen Zahlen in geordneter Weise entlang der Linie geschrieben. Damit Sie die Reihenfolge der Menge leicht visualisieren können, ist dieses System sehr gut für diejenigen, die diese numerische Menge lernen. Im folgenden Bild können Sie sehen, wie das Zeilenlayout aussehen würde.
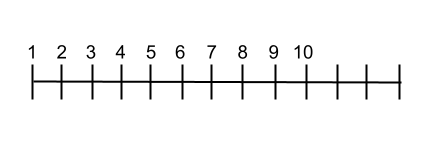
Operationen mit natürlichen Zahlen
Nachdem Sie nun alle Merkmale und Eigenschaften der Menge ℕ kennen, ist es an der Zeit, sie auf arithmetische Operationen anzuwenden, die die Hauptanwendung dieser Zahlen darstellen. Als nächstes erklären wir die vier Grundoperationen (Addition, Subtraktion, Multiplikation und Division) im Detail.
Wenn wir natürliche Werte addieren, erhalten wir eine weitere Zahl ℕ: 3 + 6 = 9 . Wenn wir jedoch zwischen natürlichen Zahlen subtrahieren, kann das Ergebnis eine positive oder negative Zahl sein. Letztere gehören nicht zu der Menge, von der wir sprechen, daher sind nur Subtraktionen, die ein positives Ergebnis haben, Teil der Menge ℕ: 4 – 2 = 2 .
Der Fall der Multiplikation zwischen natürlichen Zahlen ist derselbe wie bei der Addition, da sie nur eine positive Zahl ergeben kann. Wenn wir beispielsweise 3 und 8 multiplizieren möchten, erhalten wir 3 · 8 = 24 . Wenn wir jedoch zwischen den Zahlen in der Menge ℕ dividieren, können wir in bestimmten Fällen eine Dezimalzahl erhalten. In dieser Situation ist das Ergebnis nicht Teil des natürlichen Ganzen.
Daher sind in der Menge der natürlichen Zahlen nur Addition und Multiplikation definiert. Diese beiden Operationen überprüfen die kommutativen und assoziativen Eigenschaften. Wenn also die Anfangszahlen natürlich sind, ergeben sie immer eine natürliche Zahl. Auf diese Weise handelt es sich um Operationen, die stets die Eigenschaften der Menge ℕ berücksichtigen.
Anwendungen natürlicher Zahlen
Natürliche Zahlen werden im Alltag häufig verwendet. Damit lässt sich beispielsweise die Länge eines Tisches messen oder die Zeit, die eine Person benötigt, um zu einem Geschäft zu gehen. Sie können auch zur Durchführung mathematischer Berechnungen wie Addition oder Subtraktion verwendet werden. Ganzzahlen können auch verwendet werden, um die Position von Objekten in einem Raum zu bestimmen, beispielsweise um Bücher auf einem Regal zu platzieren.