Multiplikation (oder produkt) von polynomen

Auf dieser Seite erfahren Sie, wie Polynome multipliziert werden. Außerdem können Sie Beispiele zur Multiplikation von Polynomen und zusätzlich Schritt für Schritt gelöste Aufgaben sehen. Schließlich erfahren Sie, welche Eigenschaften multiplizierende Polynome haben.

Um jedoch das Konzept der Multiplikation von Polynomen vollständig zu verstehen, werden wir vom einfachsten zum kompliziertesten übergehen, das heißt, wir beginnen damit, wie man ein Polynom mit einer Zahl multipliziert, und dann sehen wir, wie man ein Polynom mit multipliziert ein Monom und schließlich erklären wir, wie man zwei oder mehr Polynome miteinander multipliziert.

Ich empfehle Ihnen, diese Reihenfolge einzuhalten. Wenn Sie jedoch glauben, dass Sie die Operationen mit den vorherigen Polynomen bereits beherrschen, können Sie direkt zur Multiplikation zwischen Polynomen übergehen, indem Sie auf den Index klicken:

Multiplizieren Sie ein Polynom mit einer Zahl

Das Produkt eines Skalars (oder einer Zahl) und eines Polynoms lässt sich ganz einfach lösen: Multiplizieren Sie einfach die Zahl mit dem Koeffizienten jedes Termes des Polynoms .

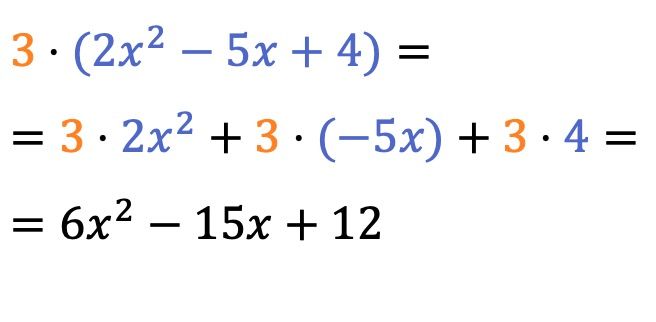
Das Multiplikationszeichen vor den Klammern kann weggelassen werden.

Multiplikation eines Polynoms mit einem Monom

Bevor wir sehen, wie man ein Polynom mit einem Monom multipliziert, erinnern wir uns zunächst daran, wie Monome miteinander multiplizieren, denn Sie müssen es wissen, um diese Art von Polynomoperation durchführen zu können.

Das Produkt zweier Monome besteht aus der Multiplikation ihrer Koeffizienten miteinander und ihrer Literalteile miteinander, das heißt, die Koeffizienten der Monome werden multipliziert und die Exponenten der Variablen mit derselben Basis addiert. Schauen Sie sich das folgende Beispiel an:

Sehen wir uns nun an, wie man ein Monom mit einem Polynom multipliziert:

Um in der Mathematik die Multiplikation eines Monoms mit einem Polynom zu lösen, wird das Monom mit jedem Term im Polynom multipliziert.

Wie bisher kann das Multiplikationszeichen auch weggelassen werden:

Beachten Sie im vorherigen Beispiel, dass Sie bei der Multiplikation von Monomen oder Polynomen auch die Vorzeichenregel berücksichtigen müssen. Tatsächlich besteht ein sehr häufiger Fehler bei der Multiplikation von Monomen und Polynomen darin, dass das Vorzeichen eines Termes falsch ist.

Sicherlich haben Sie sich irgendwann, wenn Sie etwas Neues in der Mathematik gesehen haben, gefragt: Wofür ist es da ? Nun, diese Art der Multiplikation wird verwendet, um den gemeinsamen Faktor eines Polynoms zu erhalten, eine Operation, die es Ihnen ermöglicht, Polynome zu vereinfachen (sehr nützlich). Was es ist und wie der gemeinsame Faktor eines Polynoms berechnet wird, können Sie in diesem Link sehen.

Multiplikation zweier Polynome

Sobald wir wissen, wie man Polynome mit Zahlen und mit Monomen multipliziert, schauen wir uns an, was das ist und wie man Polynome mit Polynomen multipliziert.

Damit Sie genau sehen können, was diese Methode ist, lösen wir die folgende Multiplikation von Polynomen Schritt für Schritt:

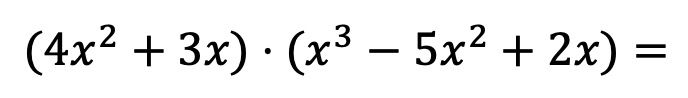
Zunächst müssen wir jedes Element des ersten Multiplikationspolynoms mit jedem Term des zweiten Polynoms multiplizieren:

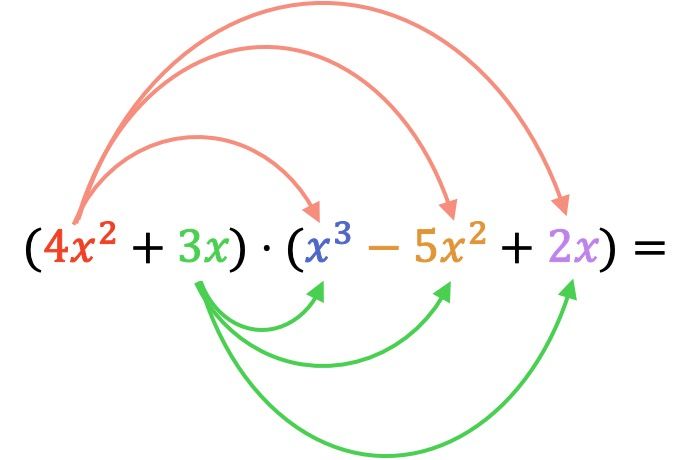
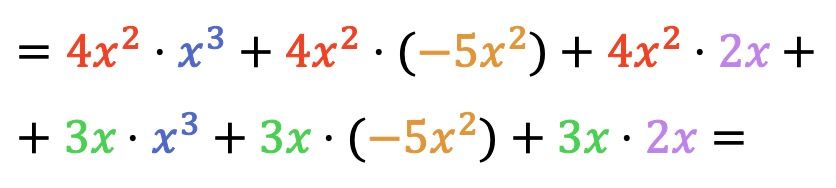
Jetzt machen wir alle Multiplikationen von Monomen:

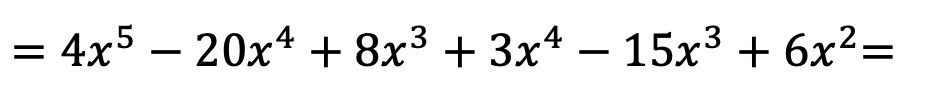
Nachdem wir die Polynome miteinander multipliziert haben, müssen wir nur noch die resultierenden Terme gruppieren, die ähnlich sind, also die Terme mit demselben Buchstaben und demselben Exponenten:

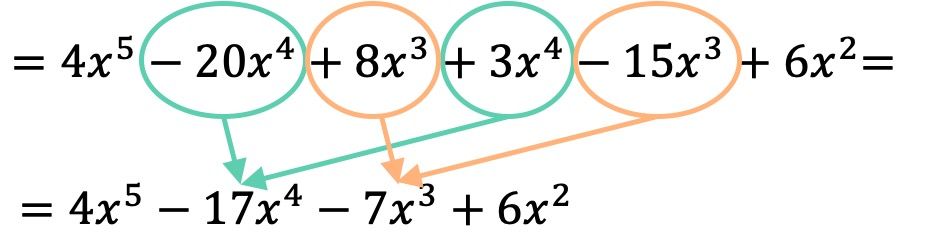
Das Ergebnis der Polynommultiplikation ist daher:

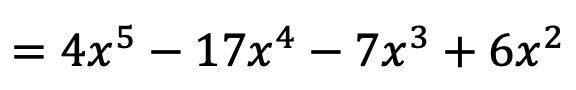
Und auf diese Weise haben wir bereits die Multiplikation von Polynomen berechnet. Vielleicht erscheint es Ihnen jetzt sehr schwierig, aber Sie werden sehen, dass es viel einfacher wird, wenn Sie mit zwei oder drei Übungen üben.

Nachdem Sie nun gesehen haben, wie die Multiplikation zwischen zwei Polynomen gelöst wird, möchten Sie wahrscheinlich wissen , wie man Polynome dividiert . Tatsächlich ist das Dividieren von Polynomen viel komplizierter als das Multiplizieren. Deshalb haben wir das Verfahren (und Tipps😉) Schritt für Schritt erklärt, damit Sie es vollständig verstehen können. Wenn Sie interessiert sind, klicken Sie auf diesen Link, um zu sehen, wie Polynome geteilt werden.

Vertikale Polynommultiplikation

Wir haben gerade gesehen, wie man ein Polynom horizontal mit einem anderen Polynom multipliziert, aber dies kann auch auf klassischere Weise erfolgen: Polynome vertikal multiplizieren. Sehen wir uns an, wie diese Methode verwendet wird, indem wir ein Beispiel einer Polynommultiplikation lösen.

Wenn wir die folgenden zwei Polynome vertikal multiplizieren wollen:

Als erstes müssen wir ein Polynom untereinander platzieren, als algebraische Multiplikation von Polynomen:

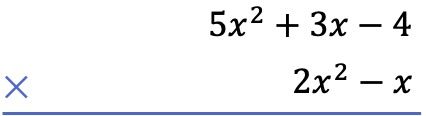
Zweitens multiplizieren wir jeden Term des Polynoms unten mit jedem Term des Polynoms oben und ordnen die Ergebnisse spaltenweise vom höchsten bis zum niedrigsten Grad an:

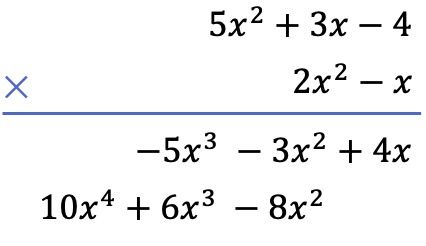
Und schließlich fügen wir die vertikal ausgerichteten Begriffe hinzu:

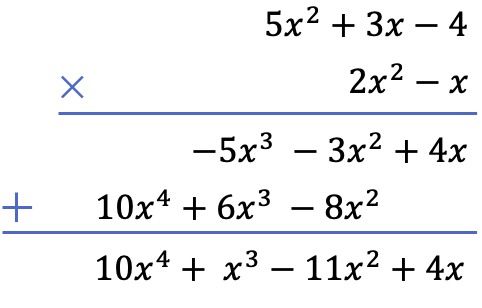
Nachdem Sie nun die beiden Methoden zur Lösung einer Multiplikation von Polynomen kennengelernt haben, wussten Sie, dass Sie auch Brüche mit Polynomen multiplizieren können ? Und nicht nur Multiplikationen, sondern alle Arten von Operationen können mit solchen Brüchen durchgeführt werden. Klicken Sie auf diesen Link und finden Sie heraus, was algebraische Brüche sind.

Eigenschaften der Polynommultiplikation

Die Multiplikation von Polynomen weist folgende Eigenschaften auf:

• Kommutative Eigenschaft : Die Reihenfolge der multiplizierenden Polynome verändert das Ergebnis der Multiplikation nicht.

• Assoziative Eigenschaft : Wenn drei oder mehr Polynome multipliziert werden, ist das Produktergebnis dasselbe, unabhängig davon, wie die Faktoren gruppiert sind:

• Verteilungseigenschaft : Die Summe zweier Polynome multipliziert mit einem dritten ist gleich der Summe jeder Addition multipliziert mit dem dritten Polynom.

• Der Grad des Polynoms , das sich aus einer Multiplikation zwischen zwei Polynomen ergibt, ist gleich der Summe der Grade der beiden multiplizierten Polynome.

Aufgaben zur Multiplikation von Polynomen gelöst

Damit Sie üben können, überlasse ich Ihnen einige gelöste Übungen zur Multiplikation von Polynomen. Sie können versuchen, sie selbst zu lösen und Ihre Ergebnisse anhand der vorgeschlagenen Lösung zu überprüfen. Anschließend können Sie uns alle Ihre Fragen in den Kommentaren stellen, wir helfen Ihnen gerne weiter.

Übung 1

Berechnen Sie die folgenden Produkte zwischen Polynomen und Skalaren:

Um die Multiplikation eines Polynoms mit einer Zahl zu berechnen, müssen Sie die Zahl mit dem Koeffizienten jedes Elements des Polynoms multiplizieren. ALSO:

Übung 2

Lösen Sie die folgenden Multiplikationen zwischen Polynomen und Monomen:

Um die Multiplikation eines Polynoms mit einem Monom zu lösen, müssen Sie das besagte Monom mit jedem Term des Polynoms multiplizieren. ALSO:

Übung 3

Bestimmen Sie das Ergebnis der folgenden Multiplikationen zwischen Polynomen:

Um eine Multiplikation zweier Polynome zu berechnen, müssen wir jedes Element des ersten Polynoms mit jedem Element des zweiten Polynoms multiplizieren und dann ähnliche Terme zusammenfassen. ALSO:

Übung 4

Finden Sie das Ergebnis der folgenden Multiplikationen zwischen Polynomen:

Um eine Multiplikation zweier Polynome zu berechnen, müssen wir jedes Element des ersten Polynoms mit jedem Element des zweiten Polynoms multiplizieren und dann die gleichen Terme addieren. ALSO:

Übung 5

Berechnen Sie die folgenden Multiplikationen von Polynomen:

Um ein Produkt aus zwei Polynomen zu erstellen, müssen Sie jeden Term des ersten Polynoms mit jedem Term des zweiten Polynoms multiplizieren und dann die erhaltenen ähnlichen Monome gruppieren. Noch:

Übung 6

Lösen Sie die folgende Multiplikation von 3 Polynomen:

Die Operation des Problems besteht aus 2 Multiplikationen von Polynomen, genauer gesagt aus zwei Binomialen und einem Trinom. Wir müssen also zunächst nach einem Produkt auflösen und dann das Ergebnis mit dem verbleibenden Polynom multiplizieren.

Wir berechnen daher die erste Multiplikation:

Und nun lösen wir die verbleibende Multiplikation:

Übung 7

Multiplizieren Sie die folgenden Polynome mit rationalen Koeffizienten (mit Brüchen):

Obwohl Polynome Brüche haben, handelt es sich dennoch um eine Multiplikation zwischen zwei Polynomen. Es muss daher wie jedes Polynomprodukt gelöst werden: Multiplizieren Sie alle Elemente miteinander und gruppieren Sie dann ähnliche Monome.

Wir multiplizieren daher die Polynome:

Und schließlich addieren (oder subtrahieren) wir die Begriffe, deren wörtliche Teile identisch sind:

Um diese Übung erfolgreich abzuschließen, war es wichtig, dass Sie die Operationen mit Brüchen beherrschen. Wenn Sie jedoch Fragen zu einem Schritt haben, können Sie diese in den Kommentaren stellen und wir werden sie so schnell wie möglich beantworten.