Auf dieser Seite erfahren Sie, wie Sie Matrizen mit den Dimensionen 2×2, 3×3, 4×4 usw. multiplizieren . Wir erklären Ihnen das Verfahren der Matrizenmultiplikation Schritt für Schritt anhand eines Beispiels, anschließend finden Sie gelöste Aufgaben, damit Sie diese auch üben können. Abschließend erfahren Sie, wann zwei Matrizen nicht multipliziert werden können und welche Eigenschaften diese Matrixoperation hat.
Wie multipliziert man zwei Matrizen?
Sehen wir uns die Vorgehensweise zur Durchführung der Multiplikation zweier Matrizen anhand eines Beispiels an:
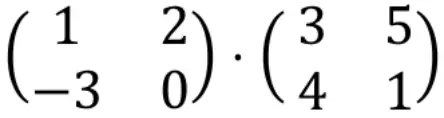
Um eine Matrixmultiplikation zu berechnen, müssen die Zeilen der linken Matrix mit den Spalten der rechten Matrix multipliziert werden.
Zuerst müssen wir also die erste Zeile mit der ersten Spalte multiplizieren. Dazu multiplizieren wir jedes Element in der ersten Zeile nacheinander mit jedem Element in der ersten Spalte und addieren die Ergebnisse. All dies wird also das erste Element der ersten Zeile des resultierenden Arrays sein. Schauen Sie sich das Verfahren an:
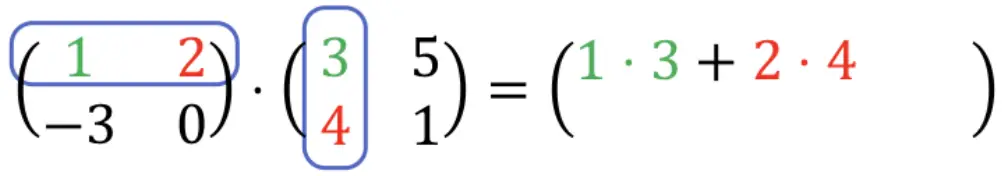
1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. Also:
Jetzt müssen wir die erste Zeile mit der zweiten Spalte multiplizieren. Deshalb wiederholen wir den Vorgang: Wir multiplizieren jedes Element der ersten Zeile einzeln mit jedem Element der zweiten Spalte und addieren die Ergebnisse. Und all dies wird das zweite Element der ersten Zeile des resultierenden Arrays sein:
1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. Also:
Sobald wir die erste Zeile der resultierenden Matrix gefüllt haben, gehen wir zur zweiten Zeile über. Wir multiplizieren daher die zweite Zeile mit der ersten Spalte, indem wir den Vorgang wiederholen: Wir multiplizieren eins nach dem anderen jedes Element der zweiten Zeile mit jedem Element der ersten Spalte und addieren die Ergebnisse:
-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. Noch:
Zum Schluss multiplizieren wir die zweite Zeile mit der zweiten Spalte . Immer mit dem gleichen Verfahren: Wir multiplizieren jedes Element der zweiten Zeile einzeln mit jedem Element der zweiten Spalte und addieren die Ergebnisse:
-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. Noch:
Und hier endet die Multiplikation der beiden Matrizen. Wie Sie gesehen haben, müssen Sie die Zeilen mit den Spalten multiplizieren und dabei immer den gleichen Vorgang wiederholen: Multiplizieren Sie jedes Element der Zeile nacheinander mit jedem Element der Spalte und addieren Sie die Ergebnisse.
Aufgaben zur Matrixmultiplikation gelöst
Übung 1
Lösen Sie das folgende Matrixprodukt:
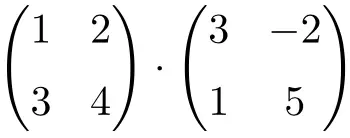
Es ist ein Produkt von Matrizen der Ordnung 2:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-747926b92c1d388c1150613b0f471d7e_l3.png)
Um ein Matrixprodukt zu lösen, müssen Sie die Zeilen der linken Matrix mit den Spalten der rechten Matrix multiplizieren.
Also multiplizieren wir zunächst die erste Zeile mit der ersten Spalte. Dazu multiplizieren wir jedes Element in der ersten Zeile nacheinander mit jedem Element in der ersten Spalte und addieren die Ergebnisse. Und all dies wird das erste Element der ersten Zeile des resultierenden Arrays sein:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eff23eaf91738d6ffb383949e4b70856_l3.png)
Jetzt multiplizieren wir die erste Zeile mit der zweiten Spalte, um das zweite Element der ersten Zeile der resultierenden Matrix zu erhalten:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-558838bcc38efc1aeeaf298d3e7151dc_l3.png)
Wir gehen zur zweiten Zeile, also multiplizieren wir die zweite Zeile mit der ersten Spalte:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-daab54a49cc53c320bb2965f691fd7ed_l3.png)
Zum Schluss multiplizieren wir die zweite Zeile mit der zweiten Spalte , um das letzte Element der Tabelle zu berechnen:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a85e0d62a0db18c7712fd1b354f92bd5_l3.png)
Das Ergebnis der Matrixmultiplikation ist also:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76f1283db0175bc1a95b0a10c8961761_l3.png)
Übung 2
Finden Sie das Ergebnis der folgenden 2×2-Quadratmatrix-Multiplikation:
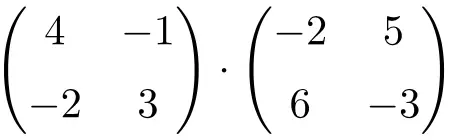
Es ist ein Produkt von Matrizen der Dimension 2×2.
Um die Multiplikation zu lösen, müssen Sie die Zeilen der linken Matrix mit den Spalten der rechten Matrix multiplizieren:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc7217dab49f67df2a9d2abc561baf9d_l3.png)
Übung 3
Berechnen Sie die folgende 3×3-Matrixmultiplikation:
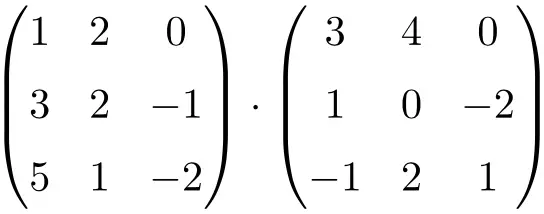
Um eine 3×3-Matrixmultiplikation durchzuführen, müssen Sie die Zeilen der linken Matrix mit den Spalten der rechten Matrix multiplizieren:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef6ee7bb6e4ac095a9fd51a545b163b0_l3.png)
Übung 4
gegeben die Matrix
![]()
:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-27365f9993caf4fcdb747352e4ae539d_l3.png)
Berechnung:
![]()
Wir berechnen zunächst die Transponierungsmatrix von
![]()
um die Multiplikation durchzuführen. Und um die Transponierungsmatrix zu erstellen, müssen wir die Zeilen in Spalten umwandeln. Das heißt, die erste Zeile der Matrix wird zur ersten Spalte der Matrix und die zweite Zeile der Matrix wird zur zweiten Spalte der Matrix. Noch:
![Rendered by QuickLaTeX.com \displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac4785c47f2e48e15b3d98ba426848b6_l3.png)
Die Matrixoperation bleibt daher:
![Rendered by QuickLaTeX.com \displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9513fa8cc6996e18e3cf287f0210817a_l3.png)
Jetzt können wir die Berechnungen durchführen. Wir rechnen zunächst
![]()
(obwohl wir auch zuerst berechnen können
![]()
):
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae5e95f09aedac8f0861bf13fb9c78a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24c003b8da1081d6ca494adc3356b06b_l3.png)
Und schließlich lösen wir das Produkt von Matrizen:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-0eb8f1817f0163a82ae39cc6c81d478e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-33533be747b72497915048e486d16541_l3.png)
Übung 5
Betrachten Sie die folgenden Matrizen:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e26aec2eee6bcae0e344682d20038f2_l3.png)
Berechnung:
![]()
Es handelt sich um eine Operation, die Subtraktion mit Matrixmultiplikationen der Ordnung 2 kombiniert:
![Rendered by QuickLaTeX.com \displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-43f79f2d970bb02caaeddec34d5ad2a1_l3.png)
Wir berechnen zunächst die Multiplikation links:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-05ff586671fb0af274884169c54e5817_l3.png)
![Rendered by QuickLaTeX.com \displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-43c234a2d7aa4f9dcaf3140f617480f1_l3.png)
Nun lösen wir die Multiplikation rechts:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-552309dd1be2f69bb72633539809283b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eeac84965cc522402e869234a841ba67_l3.png)
Und schließlich subtrahieren wir die Matrizen:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-faefbc14fc49439616b3d131243eba79_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50bac6ac99e1cf6e4b77a1a8718f9fe4_l3.png)
Wann kann man zwei Matrizen nicht multiplizieren?
Nicht alle Matrizen können multipliziert werden. Um zwei Matrizen zu multiplizieren, muss die Anzahl der Spalten in der ersten Matrix mit der Anzahl der Zeilen in der zweiten Matrix übereinstimmen.
Beispielsweise kann die folgende Multiplikation nicht durchgeführt werden, da die erste Matrix drei Spalten und die zweite Matrix zwei Zeilen hat:
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8314f9238afb3676bee5c9000c02752_l3.png)
Aber wenn wir die Reihenfolge umkehren, können sie multipliziert werden. Da die erste Matrix zwei Spalten und die zweite Matrix zwei Zeilen hat:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-37d01cc99b578d3756312c3e6ff12cae_l3.png)
Eigenschaften der Matrixmultiplikation
Diese Art von Matrixoperation weist die folgenden Merkmale auf:
- Die Matrixmultiplikation ist assoziativ:
![]()
- Die Matrixmultiplikation hat auch die Verteilungseigenschaft:
![]()
- Das Produkt von Matrizen ist nicht kommutativ:
![]()
Die folgende Matrixmultiplikation liefert beispielsweise ein Ergebnis:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3e780b321b160ad4a612e608199a374b_l3.png)
Das Ergebnis des Produkts ist jedoch ein anderes, wenn wir die Reihenfolge der Multiplikation der Matrizen umkehren:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-177d78a209e5d9e18828617e4913176d_l3.png)
- Darüber hinaus ergibt jede mit der Identitätsmatrix multiplizierte Matrix dieselbe Matrix. Dies wird als multiplikative Identitätseigenschaft bezeichnet:
![]()
![]()
Zum Beispiel:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c1e72173419eb76554256cf6ccd0d2f_l3.png)
- Schließlich ist, wie Sie vielleicht schon erraten haben, jede mit der Nullmatrix multiplizierte Matrix gleich der Nullmatrix. Dies nennt man die multiplikative Eigenschaft von Null:
![]()
![]()
Zum Beispiel:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3152d82054a80d61d548e969290aea4c_l3.png)