In diesem Artikel erklären wir, wie man die Monotonie einer Funktion erkennt, d. h. wie man die Anstiegs- und Abfallintervalle einer Funktion ermittelt. Darüber hinaus können Sie mit Schritt-für-Schritt-Übungen das Wachstum und den Rückgang einer Funktion üben.
Was ist die Monotonie einer Funktion?
Eine Funktion ist in einem Intervall monoton, wenn sie die gegebene Ordnung beibehält. Es gibt fünf Arten von Monotonie:
- Monoton wachsende Funktion: wenn der Wert der Funktion an einem Punkt immer gleich oder größer als der Wert der Funktion an einem vorherigen Punkt ist.
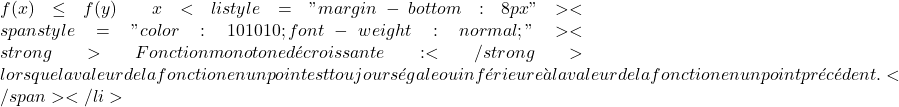Streng monoton steigende Funktion: wenn der Wert der Funktion an einem Punkt immer größer ist als der Wert der Funktion an einem vorherigen Punkt.
Konstante Funktion , wenn der Wert der Funktion an einem Punkt immer gleich dem Wert der Funktion an einem vorherigen Punkt ist.
x^2-4=0x^2=4x=\pm 2
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left( x^2-4\right)^2}f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}
f'(x)=0\cfrac{-6x}{\left(x^2-4\right)^2}=0
\left(x^2-4\right)^2}
-6x=0\cdot \left(x^2-4\right)^2-6x=0x=\cfrac{0}{-6}x=0
f'(x)=0,
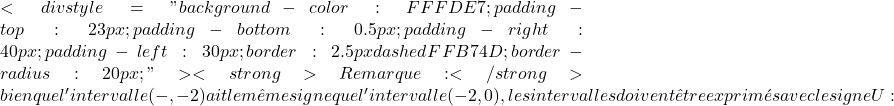
(-\infty,0)
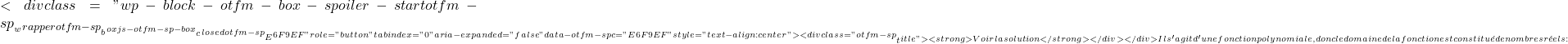
f'(x)=0.
f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9
f'(x)= 03x^2-12x+9=0\begin{aligned}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(- 12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108 }}{6} =\cfrac{12 \pm 6}{6}=\begin{cases} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6} =1 \end{cases} \end{aligned}
f'(x)=0
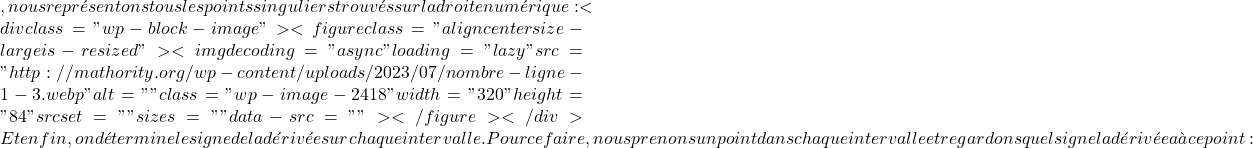
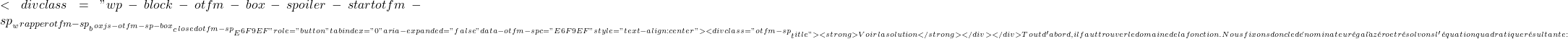
\text{Dom } f= \mathbb{R}-\{+3, -3 \}
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\ left(x^2-9\right)^2}f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}
f'(x)= 0\cfrac{-10x}{\left(x^2-9\right)^2}=0 -10x=0\cdot \left(x^2-9\right)^2 – 10x= 0 x= \cfrac{0}{-10} x=0
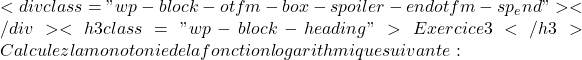
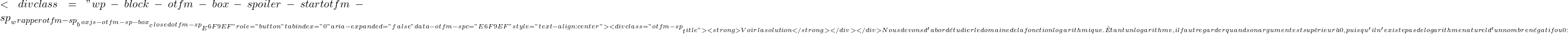
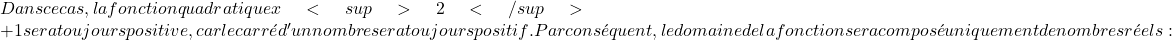
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x) = \cfrac{2x}{x^2+1}
f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \left(x^2+1\right) 2x= 0 x= \cfrac{0}{2} x=0
