Monome – Mathematik

Hier erklären wir Ihnen alles, was Sie über Monome wissen müssen: Was sie sind, was ihre Bestandteile sind (und wie man sie identifiziert), die verschiedenen Arten von Monomen, wie man Operationen mit Monomen berechnet, den numerischen Wert eines Monoms usw. .. Darüber hinaus können Sie Beispiele und Übungen sehen, die Schritt für Schritt von Monomen gelöst werden.

Was sind Monome?

In der Mathematik lautet die Definition eines Monoms wie folgt:

Ein Monom ist ein algebraischer Ausdruck, der aus einer Kombination von Zahlen und Buchstaben besteht. Genauer gesagt besteht ein Monom aus dem Produkt einer Zahl und einer oder mehreren Variablen (Buchstaben), die zu Exponenten erhöht werden.

Beispielsweise wird der Begriff 7x ³ y ² als Monom bezeichnet, weil er eine Zahl (7) und verschiedene Buchstaben (x, y) hat.

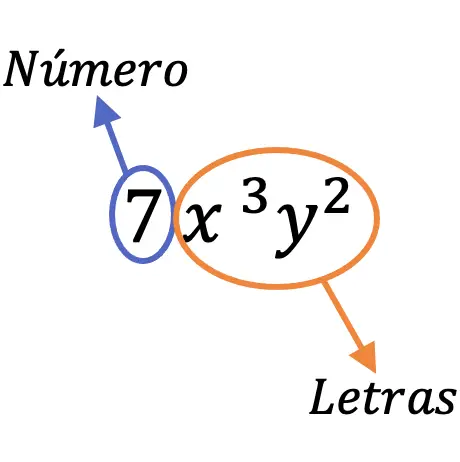
Teile eines Monoms

Nachdem wir nun die Bedeutung eines Monoms kennengelernt haben, sehen wir uns nun an, was alle Teile eines Monoms sind:

Koeffizient : ist die Zahl, die die Variablen (oder Buchstaben) des Monoms multipliziert.
Variable : ist jeder der Buchstaben, die im Monom erscheinen.
Literaler Teil : entspricht allen Variablen, aus denen das Monom besteht, mit allen ihren jeweiligen Exponenten.
Grad : besteht aus der Summe aller Exponenten der Buchstaben, die das Monom bilden.

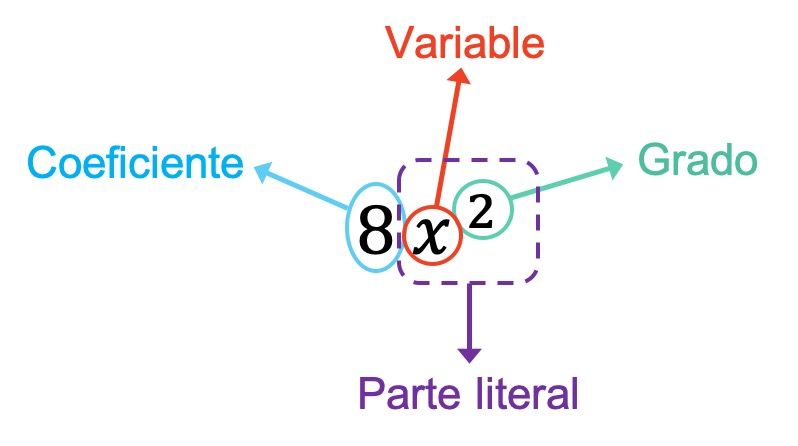
Der Koeffizient des Monoms im obigen Beispiel beträgt 8, da es sich um die Zahl handelt, die die Variablen multipliziert. Außerdem hat das Monom in diesem Fall nur eine Variable, nämlich x. Der Literalteil des Monoms wird also durch diese Variable plus ihrem Exponenten x ² gebildet. Schließlich ist der Grad des Monoms 2, da es der einzige Exponent ist, den es hat.

Versuchen Sie nun, die folgende Aufgabe auf den Teilen eines Monoms zu lösen:

Identifizieren Sie alle Teile des folgenden Monoms:

$5x^4y^2z$

siehe Lösung

Die Bestandteile des Monoms der Aussage sind:

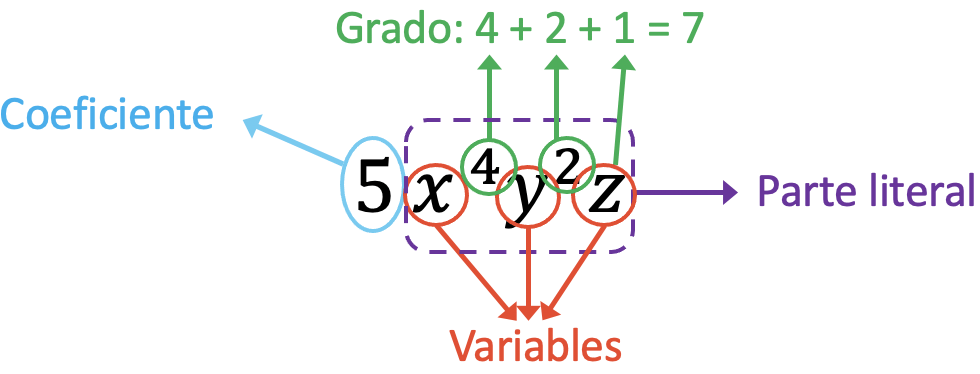
Übungen zu Monomen Schritt für Schritt gelöst

Der Koeffizient des Monoms in der Aufgabe beträgt 5, da es der Term ist, der die Buchstaben multipliziert. Andererseits sind die Variablen dieses Monoms x, y, z. Drittens entspricht der wörtliche Teil des Monoms dem Ausdruck x ⁴ y ² z. Und schließlich ist der Grad des Monoms gleich der Summe aller Exponenten der Variablen, also 7 (4+2+1=7).

Beachten Sie: Wenn ein Buchstabe keinen Exponenten hat, bedeutet dies tatsächlich, dass er eine 1 als Exponenten hat. Um den Grad des Monoms des Problems zu berechnen, fügen wir daher eine Einheit hinzu, die den Exponenten der Variablen z darstellt.

Arten von Monomen

Es gibt verschiedene Arten von Monomen mit jeweils eigenen Eigenschaften. Die wichtigsten Monome sind ähnliche Monome, homogene Monome, heterogene Monome und entgegengesetzte Monome. Als nächstes werden wir die Eigenschaften jedes Typs sehen.

homogene Monome

Zwei Monome sind homogen, wenn ihr absoluter Grad gleich ist.

Beispielsweise sind die folgenden zwei Monome homogen, weil der Grad beider gleich 5 ist:

$2x^5 \qquad \qquad 6x^2y^3$

Das erste Monom hat eine einzelne Variable, die mit 5 potenziert wird, also ist sein Grad 5. Und das zweite Polynom hat eine Variable quadriert und eine andere kubisch, also ist sein Grad ebenfalls 5 (2+ 3 =5).

Wie Sie sehen, müssen zwei Monome, um homogen zu sein, nicht denselben Literalteil haben, sondern nur denselben absoluten Grad.

heterogene Monome

Heterogene Monome sind Monome, die nicht den gleichen absoluten Grad haben. Mit anderen Worten: Heterogene Monome sind das Gegenteil von homogenen Monomen.

Die folgenden 3 Monome sind heterogen, weil jedes einen anderen Grad hat:

$x^8 \qquad 3xy \qquad 7a^9b^2$

Das erste Monom hat den Grad 8, das zweite Monom den Grad 2 und das dritte Monom den Grad 11. Daher sind die drei Monome heterogen zueinander.

Gegensätzliche Monome

Entgegengesetzte Monome sind Monome, die homogen sind (den gleichen Literalteil haben) und darüber hinaus ihre Koeffizienten entgegengesetzt sind, das heißt, ihre Koeffizienten haben den gleichen Wert, aber ein entgegengesetztes Vorzeichen.

Beispielsweise sind die folgenden zwei Monome Gegensätze:

$3x^5y^2 \qquad \qquad -3x^5y^2$

Die beiden vorherigen Monome sind Gegensätze, da sie sich nur im Vorzeichen unterscheiden, das erste hat ein positives Vorzeichen und das zweite ein negatives Vorzeichen.

Nachdem Sie nun mehrere Beispiele für Monome gesehen haben, könnte Sie ein weiterer ähnlicher algebraischer Ausdruck interessieren: das Binomial . Tatsächlich besteht ein Binomial aus der Addition (oder Subtraktion) mehrerer Monome, daher ist es interessant, die Beziehung zwischen diesen beiden Konzepten zu sehen. Sie können sehen, was die Bedeutung von Binomial ist, indem Sie auf diesen Link klicken.

Operationen mit Monomen

Um das Konzept der Monome zu vertiefen, werden wir sehen, welche Operationen mit Monomen durchgeführt werden können. Insbesondere können Monome addiert, subtrahiert, multipliziert, dividiert und potenziert werden. Und jede Art von Operation hat ihre Besonderheiten, daher werden wir sie im Folgenden einzeln analysieren.

Summe der Monome

Zwei oder mehr Monome können nur addiert werden, wenn es sich um ähnliche Monome handelt. Dann ist die Summe zweier ähnlicher Monome gleich einem anderen Monom, das aus demselben Literalteil und der Summe der Koeffizienten dieser beiden Monome besteht.

Beispiele für Summen von Monomen

$2x^4+3x^4 = 5x^4$
$4y^2+y^2 = 5y^2$
$7x^3y+2x^3y = 9x^3y$
$2a^3b^2c^6+6a^3b^2c^6 = 8a^3b^2c^6$
$4x^3+2x^3+5x^3=6x^3+5x^3=11x^3$

Wenn Sie Monomadditionsübungen üben möchten, können Sie diese in der Suchmaschine oben rechts suchen, denn wir haben eine ganze Seite voller gelöster Monomadditionsübungen.

Subtraktion von Monomen

Zwei oder mehr Monome können nur subtrahiert werden, wenn es sich um ähnliche Monome handelt. Somit ist die Subtraktion zweier ähnlicher Monome gleich einem anderen Monom, das aus demselben Literalteil besteht, und der Subtraktion der Koeffizienten dieser beiden Monome.

Beispiele für die Subtraktion von Monomen

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

Sie können mit den gelösten Schritt-für-Schritt-Übungen zur Monomsubtraktion üben, die Sie auf unserer Website finden. Sie finden sie über die Suchmaschine oben rechts.

Multiplikation von Monomen

Das Ergebnis der Multiplikation zweier Monome ist ein weiteres Monom, dessen Koeffizient das Produkt der Koeffizienten der Monome ist und dessen Literalteil durch Multiplikation der Variablen mit derselben Basis, also durch Addition ihrer Aussteller, erhalten wird.

Um das Produkt zwischen zwei verschiedenen Monomen zu lösen, müssen die Koeffizienten miteinander multipliziert und die Exponenten von Potenzen mit derselben Basis addiert werden.

Wenn wir andererseits zwei Monome mit unterschiedlicher Basispotenz multiplizieren, müssen wir einfach ihre Koeffizienten miteinander multiplizieren und die Potenzen gleich lassen:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Beispiele für die Multiplikation von Monomen

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Um mit gelösten Schritt-für-Schritt-Übungen zur Multiplikation von Monomen zu üben, können Sie den Artikel auf dieser Website lesen. Mit der Suchmaschine oben rechts finden Sie es ganz einfach.

Division von Monomen

Das Ergebnis der Division von Monomen ist ein weiteres Monom, dessen Koeffizient dem Quotienten der Koeffizienten der Monome entspricht und dessen Literalteil durch Division der Variablen mit derselben Basis, also durch Subtraktion ihrer Aussteller, erhalten wird.

Um also zwei verschiedene Monome zu dividieren, dividieren wir einfach die Koeffizienten zwischen ihnen und subtrahieren die Exponenten der Potenzen, die dieselbe Basis haben.

Beispiele für die Division von Monomen

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

Die Division von Monomen ist schwieriger als es scheint, daher empfehlen wir Ihnen, die gelösten Übungen zur Division von Monomen Schritt für Schritt durchzuführen. Am schnellsten finden Sie sie über unsere Suchmaschine oben rechts.

Potenz eines Monoms

Um die Potenz eines Monoms zu berechnen, muss jedes Element des Monoms auf den Exponenten potenziert werden . Mit anderen Worten: Die Potenz eines Monoms besteht darin, seinen Koeffizienten und seine Variablen (Buchstaben) auf den Exponenten der Potenz zu erhöhen.

Erinnern Sie sich an die Eigenschaften von Potenzen: Wenn wir einen bereits erhobenen Term erhöhen, werden die beiden Exponenten miteinander multipliziert. Aus diesem Grund wird bei der Potenz eines Monoms der Exponent jedes Buchstabens immer mit dem Exponenten multipliziert, der die Potenz angibt .

Beispiele für Potenzen von Monomen

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Bei dieser Art der Operation mit Monomen kann es recht leicht passieren, dass man einen Fehler macht. Deshalb empfehlen wir Ihnen, mit den Übungen zu üben, die wir auf unserer Website Schritt für Schritt gelöst haben . Sie finden sie schnell, indem Sie oben rechts in der Suchmaschine danach suchen.

Zahlenwert eines Monoms

Der numerische Wert eines Monoms ist das Ergebnis, das man erhält, indem man bestimmte Werte durch die Variablen eines Monoms ersetzt.

Wenn wir zum Beispiel das folgende Monom haben:

$5x^2$

Wenn wir den numerischen Wert des vorherigen Monoms für finden wollen

$x=2$

Sie müssen den Buchstaben ersetzen

$x$

des Monoms durch 2 und lösen Sie die resultierenden Operationen:

$5\cdot 2^2= 5 \cdot 4 = 20$

Also der Zahlenwert des Monoms

$5x^2$

Für

$x=2$

ist gleich 20.

Sie können auch den numerischen Wert einer monomialen Multivariablen bestimmen. Wenn wir zum Beispiel die folgende Bivariable oder mit anderen Worten ein Monom mit zwei Variablen haben:

$3x^4y$

Um den numerischen Wert des oben genannten Monoms zu berechnen, wann

$x$

im Wert von 1 e

$y$

ist -2, wir ersetzen die Buchstaben durch ihre jeweiligen Werte:

$3\cdot 1^4\cdot (-2)= 3 \cdot 1 \cdot (-2) = -6$

Also der numerische Wert des Monoms des Problems für

$x=1$

Und

$y=-2$

gibt -6 zurück.

Monome und Polynome

Schließlich wissen Sie, dass Polynome aus Monomen gebildet werden können:

Ein Polynom ist die Gruppierung von zwei oder mehr Monomen.

$P(x)= 4x^5+3x^2-7x$

Das vorherige Polynom ergibt sich beispielsweise aus der Addition (oder Subtraktion) von 3 heterogenen Monomen.

Wenn ein Polynom nur zwei Monome hat, wird es aus Neugier als Binomial bezeichnet. Und wenn ein Polynom genau drei Monome hat, nennt man es ein Trinom .

Wenn Sie mehr über Polynome erfahren möchten, können Sie die Hauptseite des Internets besuchen, wo wir Ihnen alles erklären, was Sie über Polynome wissen müssen.