So berechnen Sie den Modul eines Vektors

Auf dieser Seite sehen Sie die Erklärung der Größe eines Vektors und wie man ihn mit seiner Formel berechnet. Sie können auch sehen, wie Sie das Modul von zwei Punkten aus finden: seinem Ursprung und seinem Ende. Darüber hinaus erfahren Sie, wie Sie die Komponenten eines Vektors aus seinem Modul und den Eigenschaften des Moduls eines Vektors bestimmen. Sie können sogar mit Beispielen, Übungen und Schritt-für-Schritt-Aufgaben üben.

Was ist der Modul eines Vektors?

Der Betrag eines Vektors stellt den Abstand zwischen seinem Ursprung und seinem Ende dar. Daher ist die Größe eines Vektors gleich der Länge dieses Vektors.

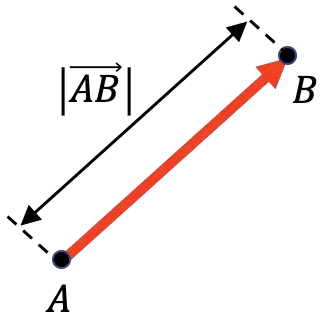
Wie Sie in der grafischen Darstellung oben sehen können, wird die Größe eines Vektors durch einen vertikalen Balken auf jeder Seite des Vektors symbolisiert:

$\lvert \vv{AB}\rvert$

Andererseits ist der Modul eines Vektors derselbe wie die Norm eines Vektors , Sie können ihn also auch so schreiben. Deshalb gibt es Mathematiker, die den Modul eines Vektors auch mit zwei vertikalen Balken auf jeder Seite darstellen:

$\lvert \lvert \vv{AB}\rvert\rvert$

Formel für den Modul eines Vektors

Um den Betrag eines Vektors in der Ebene zu ermitteln, müssen wir die folgende Formel anwenden:

Um die Größe eines Vektors zu bestimmen, müssen wir die (positive) Quadratwurzel der Summe der Quadrate seiner Komponenten berechnen. Mit anderen Worten, wenn wir den folgenden Vektor haben:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Sein Modul ist:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

Wir berechnen beispielsweise den Betrag des folgenden Vektors mit der Formel:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Berechnen Sie die Größe eines Vektors anhand der Koordinaten seines Ursprungs und Endes

Wir haben gerade gesehen, wie die Größe eines Vektors bestimmt wird, wenn wir seine Komponenten kennen, aber was würde passieren, wenn wir nur die Punkte kennen würden, an denen er beginnt und wo er endet?

Um also die Größe eines Vektors aus den Koordinaten seines Ursprungs und seines Endes zu berechnen, müssen Sie diese beiden Schritte befolgen:

Zuerst finden wir die Komponenten des Vektors. Dazu müssen wir das Extremum minus den Ursprung subtrahieren.
Und dann berechnen wir den Modul des erhaltenen Vektors mit der Formel, die wir im vorherigen Abschnitt gesehen haben.

Sehen wir uns anhand eines Beispiels an, wie das geht:

Berechnen Sie den Betrag des Vektors, dessen Ursprung der Punkt ist
$A(2,1)$

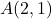
und als letzter Punkt

$B(-1,4).$

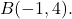
Zuerst müssen wir die Komponenten des Vektors finden, also subtrahieren wir seinen Endpunkt minus seinen Ursprung:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Sobald wir den Vektor kennen, berechnen wir seine Größe mithilfe der Vektorgrößenformel:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

Und wir belassen das Ergebnis als Quadratwurzel, weil es nicht exakt ist.

So berechnen Sie die Komponenten eines Vektors aus seinem Modul

Wir haben gesehen, wie man die Größe eines Vektors aus seinen Komponenten extrahiert, aber der Prozess kann auch umgekehrt werden. Mit anderen Worten: Wir können die Komponenten eines Vektors über seinen Modul berechnen.

Der Prozess, die Komponenten eines Vektors aus seiner Größe zu ermitteln, wird als Vektorzerlegung bezeichnet. Um einen Vektor zu zerlegen, benötigen wir also natürlich seine Größe und den Winkel, den er mit der Abszissenachse (X-Achse) bildet.

Damit die X- und Y-Komponenten des Vektors mit den trigonometrischen Verhältnissen berechnet werden können:

Wie Sie im Bild sehen können, bildet der Betrag eines Vektors mit seinen Komponenten ein rechtwinkliges Dreieck, sodass die Elementarformeln der Trigonometrie angewendet werden können.

Es muss berücksichtigt werden, dass seine Komponenten im Gegensatz zum Modul eines Vektors negativ sein können, da Sinus und Cosinus negative Werte annehmen können.

Als Beispiel lösen wir die Vektorzerlegung des Vektors, dessen Betrag und Winkel mit der OX-Achse sind:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

Die horizontale Komponente des Vektors ist gleich dem Modul multipliziert mit dem Kosinus des Winkels:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

Und die vertikale Komponente des Vektors ist gleich der Multiplikation des Moduls mit dem Sinus des Winkels:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

Der Vektor ist also der folgende:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Moduleigenschaften eines Vektors

Modulus ist eine Art Vektoroperation mit den folgenden Merkmalen:

Der Betrag eines Vektors kann niemals negativ sein , er wird immer gleich oder größer als 0 sein.

$\lvert \vv{\text{u}} \rvert \geq 0$

Tatsächlich ist der einzige Vektor, der mit der Größe Null existiert, der Nullvektor, d. h. der Vektor

$\vv{\text{u}}= (0,0) .$

Der Betrag des Produkts eines Vektors mit einer reellen Zahl (oder einem Skalar) entspricht der Multiplikation des Absolutwerts des Skalars mit dem Betrag des Vektors. Daher gilt folgende Gleichheit:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

Die Dreiecksungleichung ist verifiziert: Der Modul der Summe zweier Vektoren ist kleiner oder gleich der Summe ihrer Module einzeln.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

Darüber hinaus hängt die Größe der Summe zweier Vektoren durch die folgende Gleichung mit dem Skalarprodukt zusammen:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

Einheitsvektor

In der Mathematik ist ein Einheitsvektor ein Vektor, dessen Modul gleich eins ist.

$\lvert \vv{\text{u}} \rvert=1$

Daher beträgt die Länge eines Einheitsvektors eine Einheit.

Es mag für einen Vektor sehr schwierig erscheinen, einen Modul von genau 1 zu haben, aber es ist tatsächlich einfach, diesen Vektortyp zu finden:

Um den Einheitsvektor eines beliebigen Vektors zu finden, dividieren Sie ihn einfach durch seinen Modul:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Gold

$\vv{\text{v}}_u$

ist der Einheitsvektor von

$\vv{\text{v}},$

Und

$\lvert \vv{\text{v}} \rvert$

Ihr Modul.

Der Einheitsvektor wird auch Versor oder normalisierter Vektor genannt.

Darüber hinaus hat der Einheitsvektor die gleiche Richtung und Richtung wie der ursprüngliche Vektor.

Beispielsweise berechnen wir den Einheitsvektor des folgenden Vektors:

$\vv{\text{v}}=(1,-1)$

Um den Vektor zu normalisieren, müssen wir zunächst seinen Betrag berechnen:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

Und schließlich berechnen wir den Einheitsvektor, indem wir den ursprünglichen Vektor durch seinen Modul dividieren:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Übungen zum Vektormodul gelöst

Übung 1

Berechnen Sie den Betrag des folgenden Vektors:

$\vv{a}=(6,8)$

siehe Lösung

Um den Modul des Vektors zu berechnen, müssen wir seine Formel anwenden:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Übung 2

Ordnen Sie die folgenden Vektoren vom kürzesten zum längsten.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

siehe Lösung

Die Länge eines Vektors entspricht seinem Betrag. Daher müssen wir die Moduli aller Vektoren berechnen:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

Somit sind die von der kleinsten zur größten Länge (oder dem größten Modul) geordneten Vektoren:

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Übung 3

Bestimmen Sie den Betrag des Vektors, dessen Ursprung der Punkt ist

$A(-3,2)$

und als letzter Punkt

$B(7,-4).$

siehe Lösung

Um seinen Modul zu berechnen, müssen Sie zunächst den Vektor finden. Dazu subtrahieren wir das Extremum minus den Ursprung:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Sobald wir den Vektor kennen, wird sein Modul mithilfe der Modulformel berechnet:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Übung 4

Zerlegen Sie den folgenden Vektor und finden Sie seine Komponenten:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

siehe Lösung

Die horizontale Komponente des Vektors ist gleich dem Modul multipliziert mit dem Kosinus des Winkels:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

Und die vertikale Komponente des Vektors ist gleich der Multiplikation des Moduls mit dem Sinus des Winkels:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

Der Vektor ist also der folgende:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

In diesem Fall sind die beiden Komponenten identisch, d. h. der Neigungswinkel des Vektors beträgt 45°.

Übung 5

Berechnen Sie den Vektor mit derselben Richtung und Ausrichtung wie der folgende Vektor, jedoch mit Modul 1.

$\vv{a} = (-4,3)$

siehe Lösung

Der Vektor mit gleicher Richtung und gleicher Richtung, aber mit Modul 1 ist der Einheitsvektor. Um es zu berechnen, ermitteln wir zunächst den Modul des Vektors:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$

Und jetzt berechnen wir den Einheitsvektor, indem wir den ursprünglichen Vektor durch seinen Modul dividieren:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(-4,3)}{5}= \bm{\left(-\frac{4}{5},\frac{3}{5} \right)}$

Übung 6

Zerlegen Sie den folgenden Vektor vektoriell und berechnen Sie seinen Einheitsvektor:

$\lvert \vv{a} \rvert =6 \qquad \alpha = 20º$

siehe Lösung

Zuerst zerlegen wir den Vektor und finden seine Koordinaten:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(20º)= 6 \cdot 0,94 = 5,64$

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(20º)= 6 \cdot 0,34 = 2,05$

Der Vektor ist also der folgende:

$\vv{a}= (5,64 \ ,\ 2,05)}$

Und jetzt berechnen wir den Einheitsvektor, indem wir den erhaltenen Vektor durch sein Modul dividieren:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(5,64 \ ,\ 2,05)}{6}= \bm{(0,94 \ , \ 0,34) }$

Beachten Sie, dass die Komponenten eines Einheitsvektors gleich dem Kosinus und Sinus des Winkels sind, den er mit der X-Achse bildet.

So berechnen sie den modul eines vektors

Was ist der Modul eines Vektors?

Formel für den Modul eines Vektors

Berechnen Sie die Größe eines Vektors anhand der Koordinaten seines Ursprungs und Endes

So berechnen Sie die Komponenten eines Vektors aus seinem Modul

Moduleigenschaften eines Vektors

Einheitsvektor

Übungen zum Vektormodul gelöst

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Übung 6

Kommentar verfassen Kommentieren abbrechen