Was ist die methode der kleinsten quadrate?

Die Methode der kleinsten Quadrate ist ein mathematisches Werkzeug zum Finden der besten geraden Linie, die einer Menge von Punkten entspricht . Wir erklären es Ihnen ganz einfach:

Stellen Sie sich vor, Sie haben eine Reihe von Punkten in einem Diagramm, die hier und da verstreut sind. Sie möchten eine gerade Linie finden, die am besten zu diesen Punkten „passt“, um den Abstand zwischen der Linie und den Punkten zu minimieren . Dies ist die Idee hinter der Methode der kleinsten Quadrate.

Die Methode verwendet eine Formel zur Berechnung der Geradengleichung, die die Summe der Quadrate der Differenzen zwischen den Punkten und der Geraden minimiert. Das heißt, es wird nach der Linie gesucht, die die geringste „Abweichung“ von den Punkten aufweist.

Einfach ausgedrückt ist die Methode der kleinsten Quadrate nützlich für die Analyse von Daten, die während einer Untersuchung gewonnen wurden, mit dem Ziel, ihr Verhalten linear auszudrücken und so die Fehler der gestohlenen Informationen zu reduzieren.

Wer hat die Methode der kleinsten Quadrate entwickelt?

Die Methode der kleinsten Quadrate, ein grundlegendes Werkzeug in der Statistik und Datenanalyse, wird dem deutschen Mathematiker Carl Friedrich Gauß zugeschrieben, der sie 1794 vorschlug. Gauß veröffentlichte sie jedoch erst 1809 .

Interessanterweise veröffentlichte der französische Mathematiker Andrien-Marie Legendre 1805 eine ähnliche Version und entwickelte sie unabhängig weiter.

Beide Mathematiker haben an der Entwicklung dieser Methode mitgewirkt, die in verschiedenen Disziplinen weit verbreitet ist, um Modelle an beobachtete Daten anzupassen und genaue Vorhersagen zu treffen.

Formel der kleinsten Quadrate

Um zu verstehen, was diese Methode beinhaltet, ist es zweifellos wichtig, ihre Formel und den Prozess ihrer Umsetzung zu erklären. Hier ist eine detaillierte Erklärung der Formel der kleinsten Quadrate:

definiere das Problem

Nehmen wir an, Sie haben einen Datensatz mit zwei Variablen, einer unabhängigen Variablen (x) und einer abhängigen Variablen (y), und Sie möchten eine gerade Linie an diese Daten anpassen.

Das Ziel besteht darin, die Werte der Koeffizienten der Geradengleichung (Achsenabschnitt und Steigung) zu finden, die die Summe der Quadrate der Differenzen zwischen den realen Werten von y und den von ihr vorhergesagten Werten minimiert angepasste Linie.

Berechnen Sie die Gleichung der Geraden

Die Gleichung einer Geraden hat die Form y = mx + b, wobei m die Steigung und b der y-Achsenabschnitt ist. Die Formel der kleinsten Quadrate zur Berechnung der Myb-Werte lautet:

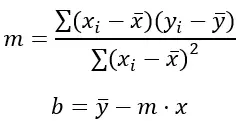
Gold:

Σ stellt die Summe der Werte dar.

x _i und y _i sind die Werte der Variablen x bzw. y für jeden Datenpunkt.

x̄ und ȳ sind die Durchschnittswerte der Werte von x bzw. y.

(x _i – x̄) und (y _i – ȳ) sind die Unterschiede zwischen den Werten von x und y und ihren jeweiligen Mittelwerten.

(x _i – x̄) ² ist das Quadrat der Differenz zwischen dem Wert von x und seinem Mittelwert.

Interpretieren Sie die Ergebnisse

Nachdem Sie die Werte von m und b mithilfe der Formel berechnet haben, können Sie diese verwenden, um die Gleichung der angepassten Linie zu erhalten. Wenn Sie beispielsweise m = 2 und b = 3 haben, lautet die Gleichung der angepassten Linie y = 2x + 3. Dadurch können Sie Vorhersagen oder Schätzungen der y-Werte für verschiedene x-Werte treffen basierend auf dem angepassten Recht.

Wann wird die Methode der kleinsten Quadrate verwendet?

Sie werden sich wahrscheinlich fragen: Wann wird diese Methode angewendet? Es ist in verschiedenen Situationen sehr nützlich! Zum Beispiel, wenn Sie experimentelle oder Forschungsdaten analysieren möchten, um einen Zusammenhang oder Trend zu finden .

Angenommen, Sie untersuchen den Zusammenhang zwischen dem Preis eines Hauses und seiner Größe in Quadratmetern. Sie können die Methode der kleinsten Quadrate verwenden, um die gerade Linie zu finden, die am besten zu den Daten passt und Ihnen eine klare Vorstellung von dieser Beziehung gibt.

Es wird auch in der Wirtschaftswissenschaft verwendet, um Variablen wie Produktnachfrage oder Preisverhalten zu modellieren und vorherzusagen . Darüber hinaus wird im Ingenieurwesen die Methode der kleinsten Quadrate angewendet, um mathematische Modelle an Test- oder Simulationsdaten anzupassen.

Die Methode der kleinsten Quadrate ist ein leistungsstarkes und vielseitiges Werkzeug, das in vielen Studien- und Arbeitsbereichen zur Datenanalyse und zum Auffinden wichtiger Zusammenhänge eingesetzt wird.

Anwendungen der Methode der kleinsten Quadrate in anderen Theoremen

Zusätzlich zu ihrer Verwendung an sich ist die Methode der kleinsten Quadrate auch in anderen Theoremen sehr nützlich. Sehen wir uns weiter unten etwas mehr zu diesem Thema an.

Regressionssatz

Es wird häufig im Regressionssatz verwendet, um die beste Linie zu finden, die zu einem Datensatz passt . Sie können damit beispielsweise die Beziehung zwischen der Höhe einer Pflanze und der Menge an Licht, die sie erhält, analysieren, um zu bestimmen, wie die Pflanze bei unterschiedlichen Lichtverhältnissen wächst.

Satzinterpolation

In diesem Fall wird die Methode der kleinsten Quadrate auch im Interpolationssatz angewendet, um die Polynomfunktion zu finden , die am besten zu einer Menge von Punkten passt. Sie können damit beispielsweise die Flugbahn eines sich bewegenden Objekts anhand von Positions- und Zeitdaten annähern.

Kurvenanpassungssatz

Es wird im Kurvenanpassungssatz verwendet, um eine Kurve zu finden, die zu einem Datensatz passt . Dies ist nützlich bei Anwendungen wie der Modellierung von Klimadaten zur Vorhersage des Klimawandels oder zur Vorhersage der Flugbahn eines Projektils.

Satz der Fourier-Analyse

Im Fourier-Analyse-Theorem wird die Methode der kleinsten Quadrate verwendet, um eine periodische Funktion aus einer Reihe diskreter Daten anzunähern . Dies gilt für die Datensignalisierung sowie die Bild- und Tonkomprimierung.

Nichtlinearer Regressionssatz

Schließlich wird die Methode der kleinsten Quadrate auch im nichtlinearen Regressionssatz angewendet, um die beste Kurve zu finden, die zu einem Datensatz passt , der keiner linearen Beziehung folgt . Sie können damit beispielsweise analysieren, wie sich die Konzentration einer Chemikalie auf die Reaktionsgeschwindigkeit auswirkt.

Beispiel für die Methode der kleinsten Quadrate

Um besser zu verstehen, wie Sie die Methode der kleinsten Quadrate anwenden können, schauen wir uns unten ein Beispiel an.

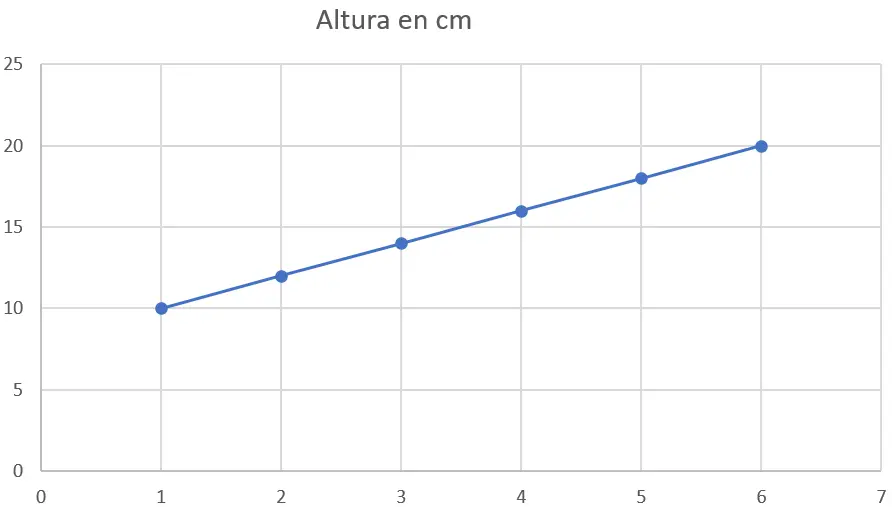
Angenommen, Sie haben die folgenden Höhendaten (in Zentimetern) einer Pflanze in verschiedenen Wochen:

Woche	Höhe in Zentimetern
1	zehn
2	12
3	14
4	16
5	18
6	zwanzig

Sie möchten die beste gerade Linie finden, die zu diesen Daten passt, um eine Vorhersage über die zukünftige Pflanzenhöhe zu treffen.

Schritt 1 : Stellen Sie die Daten grafisch dar

Als erstes müssen Sie die Daten in einem Streudiagramm darstellen. Die x-Achse stellt die Wochen dar und die y-Achse die Körpergröße in Zentimetern. Hier ist die Grafik:

Schritt 2 : Wenden Sie die Methode der kleinsten Quadrate an

Die Methode der kleinsten Quadrate versucht, eine Linie zu finden, die die Summe der Quadrate der Differenzen zwischen den tatsächlichen Daten und den durch die Linie vorhergesagten Werten minimiert. In diesem Fall wird die Linie durch die Gleichung einer Linie dargestellt: y = mx + b, wobei „y“ die Höhe, „x“ die Wochen, „m“ die Steigung der Linie und „b“ ist der y-Achsenabschnitt.

Um die Werte von „m“ und „b“ zu finden, die die Summe der Quadrate der Differenzen minimieren, werden die folgenden Formeln verwendet:

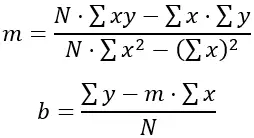
Dabei ist N die Anzahl der Datenpunkte (in diesem Fall 6), Σxy die Summe der Wochen mal den Höhen, Σx die Summe der Wochen, Σy die Summe der Höhen und Σx ² die Summe der Quadrate der Wochen .

Wenn wir diese Formeln auf die Höhendaten anwenden, erhalten wir:

Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630

Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21

Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90

Σx ² = 1 ² + 2 ² + 3 ² + 4 ² + 5 ² + 6 ² = 91

Einsetzen dieser Werte in die Formeln für „m“ und „b“:

m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 ² ) ≈ 2,07

b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24

Daher lautet die Gleichung der geraden Linie, die den Höhendaten entspricht: y.