Nilpotente Matrix

Auf dieser Seite finden Sie eine Erklärung, was eine nilpotente Matrix ist, sowie mehrere Beispiele, damit Sie sie verstehen und keine Zweifel haben können. Darüber hinaus können Sie die Strukturen nullpotenter Matrizen und alle Eigenschaften dieser Matrizentypen sehen.

Was ist eine nilpotente Matrix?

Die Definition einer nilpotenten Matrix lautet wie folgt:

Eine nilpotente Matrix ist eine quadratische Matrix, die auf eine ganze Zahl erhöht die Nullmatrix ergibt.

$N^k =0$

Gold

$N$

ist die nilpotente Matrix und

$k$

der Exponent der Potenz, die die Nullmatrix ergibt.

Diese Bedingung bedeutet nicht, dass die Potenz einer nilpotenten Matrix unabhängig vom Exponenten immer Null ergibt, sondern vielmehr, dass die Matrix nullpotent ist, wenn es mindestens eine Potenz der Matrix gibt, deren Ergebnis eine Matrix voller Nullen ist.

Andererseits ist der Nullpotenzindex einer Nullpotenzmatrix die kleinste Zahl, mit der die Nullpotenzbedingung erfüllt ist. Wir können auch sagen, dass die Nullpotenzmatrix die Ordnung k hat, wobei k ihr Nullpotenzindex ist.

Beispiele für nilpotente Matrizen

Um das Konzept einer nilpotenten Matrix vollständig zu verstehen, sehen wir uns einige Beispiele für diesen Matrixtyp an:

Beispiel einer 2 × 2 nilpotenten Matrix

Die folgende quadratische Matrix der Dimension 2×2 ist nilpotent:

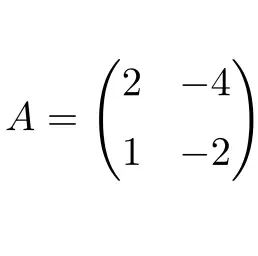
Beispiel einer nilpotenten Matrix der Dimension 2x2

Die Matrix ist nullpotent, da wir durch Quadrieren der Matrix A die Nullmatrix als Ergebnis erhalten:

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

Es handelt sich also um eine nullpotente Matrix und ihr Nullpotenzindex beträgt 2, da die Nullmatrix bis zur zweiten Potenz erhalten wird.

Beispiel einer 3×3 nullpotenten Matrix

Die folgende quadratische Matrix der Ordnung 3 ist nilpotent:

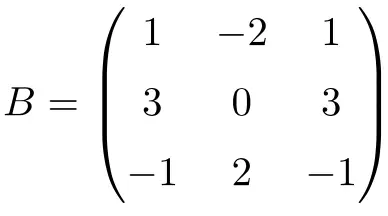
Beispiel einer nilpotenten Matrix der Dimension 3x3

Obwohl wir durch die Erhöhung der Matrix auf 2 nicht die Nullmatrix erhalten:

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Aber wenn wir den Würfel der Matrix berechnen, erhalten wir eine Matrix, bei der alle Elemente gleich 0 sind:

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

Matrix B ist also eine nilpotente Matrix, und da die Nullmatrix hoch 3 erhalten wird, beträgt ihr Nullpotenzindex 3.

Struktur einer 2 × 2 nilpotenten Matrix

Unten sehen Sie die Struktur aller nilpotenten Matrizen. Der Beweis ist etwas mühsam, daher überlassen wir Ihnen direkt die Formel, um eine nilpotente Matrix der Ordnung 2 zu erhalten:

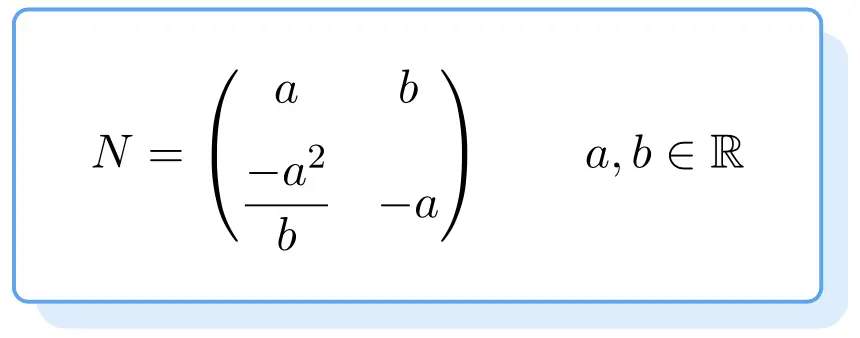
Struktur und Formel einer 2x2 nilpotenten Matrix

Jede Matrix, die die obige Formel erfüllt, ist also eine nilpotente Matrix. Hierzu die Werte

$a$

Und

$b$

Sie können beliebig sein, solange es sich um reelle Zahlen handelt.

Eigenschaften nilpotenter Matrizen

Nilpotente Matrizen haben die folgenden Eigenschaften:

Die Spur einer nilpotenten Matrix ist immer Null.

Ebenso ist die Determinante jeder nilpotenten Matrix immer 0. Das Gegenteil ist jedoch nicht der Fall, dh die Determinante einer Matrix ist Null, was nicht bedeutet, dass die Matrix nilpotent ist.

Die einzige nullpotente Matrix, die diagonalisiert werden kann, ist die Nullmatrix.

Der Nullpotenzindex einer Nullpotenzmatrix der Dimension n×n ist immer gleich oder kleiner als n . Aus diesem Grund beträgt der Nullpotenzindex einer 2 × 2-Nullpotenzmatrix immer 2.

Eine nilpotente Matrix ist nicht invertierbar.

Jede Dreiecksmatrix mit Nullen auf der Hauptdiagonalen ist ebenfalls eine nilpotente Matrix.

Es gibt einen Satz, der besagt, dass wenn die Matrix
$N$

nullpotent ist, dann ist die Matrix

$N+I$

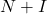
ist invertierbar, wo

$I$

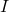
ist die Identitätsmatrix. Darüber hinaus kann die inverse Matrix mit der folgenden Formel ermittelt werden:

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

Äquivalent, wenn
$N$

eine nilpotente Matrix ist, kann die Umkehrung der Matrix berechnet werden

$N-I$

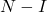
mit der folgenden Gleichung:

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Jede singuläre, also nicht invertierbare Matrix kann in das Produkt nullpotenter Matrizen zerlegt werden.

Alle Eigenwerte (oder Eigenwerte) einer nilpotenten Matrix sind Null.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

Als Kuriosität gibt es schließlich auch das Konzept der nilpotenten Transformation, das eine lineare Anwendung definiert
$L$

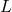
eines Vektorraums, so dass

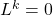
$L^k=0$

.