Magic Squares ist ein Mathe-Puzzlespiel, das unsere Rechenfähigkeiten auf unterhaltsame und spannende Weise trainiert. Deshalb ist es eine der besten Ressourcen für den Mathematikunterricht für junge Schüler.
Was ist ein Magic Array und wie wird es aufgelöst?
Ein magisches Quadrat ist eine Art Tabelle oder Matrix bestehend aus verschiedenen Kästchen, in die ganze Zahlen geschrieben werden. Sie können jedoch unter keinen Umständen installiert werden; Eine Reihe von Regeln müssen eingehalten werden:
- Alle magischen Summen (Summen aller Werte einer horizontalen, vertikalen oder diagonalen Linie) müssen immer den Wert ergeben, der der magischen Konstante entspricht (es ist ein einzelner Wert).
- Keine Zahl kann zweimal wiederholt werden.
- Sie können nur fortlaufende Zahlen (z. B. von 1 bis 9) oder Zahlen verwenden, die einer bestimmten Reihe folgen, z. B. ungerade Zahlen, Vielfache von 5 und andere.
Außerdem ist es wichtig zu betonen, dass wir Quadrate je nach ihrer Struktur unterschiedlich klassifizieren können. Die erste hängt vom Grad des Quadrats ab, der der Anzahl der Zellen entspricht, die sich in einer Zeile oder Spalte befinden. Und die zweite hängt von der Art des Tabellengrades ab ( gerade Zahlen oder ungerade Zahlen). Anhand dieser Unterscheidungen können wir alle Quadrate in verschiedene Kategorien einteilen, obwohl wir später näher darauf eingehen werden.
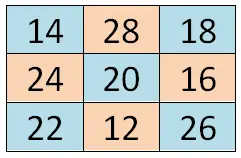
Wie löst man magische Quadrate?
Um dieses Mathe-Spiel zu lösen, können wir zwei verschiedene Methoden verwenden: die Geometrie verwenden oder die magische Konstante berechnen. Beide Vorgehensweisen sind gleichermaßen gültig, obwohl man mit der einen schneller zum Ergebnis kommt, während die andere mehr Zeit und Überlegung erfordert. Als nächstes erklären wir beide Methoden, damit Sie die von Ihnen bevorzugte auswählen und sich besser an die jeweilige Situation anpassen können.
Wie lautet die Formel für magische Quadrate?
Die erste Methode besteht in der Berechnung der magischen Konstante , für die wir die folgende Formel verwenden müssen: n(n 2 +1)/2, wobei n der Grad des Quadrats ist. Und sobald wir diesen Wert haben, müssen wir nur noch die verschiedenen Zahlenkombinationen ausprobieren, die es uns ermöglichen, die magischen Summen des gesamten Quadrats mit der Konstanten auszugleichen. Mit anderen Worten: Wir müssen Zahlenkombinationen bilden, die sich zum Wert der Konstante addieren, damit das Gesamtbild ausgeglichen ist.
Wie löst man magische Quadrate mithilfe der Geometrie?
Zweitens können wir magische Quadrate mithilfe der Geometrie lösen. Allerdings ist zu beachten, dass diese Methode sehr einfach ist und keine Rechenkenntnisse erfordert, da sie rein methodischer Natur ist. Vor diesem Hintergrund erklären wir das Verfahren zum Lösen von Quadraten gerader und ungerader Ordnung.
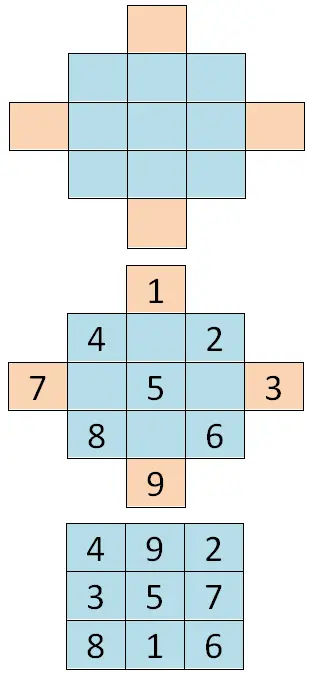
Wie löst man magische Quadrate mit ungeraden Zahlen?
Um diesen ersten Fall zu lösen, müssen Sie Zellen zur Ausgangstabelle hinzufügen, sodass eine Art Raute entsteht. Dann müssen wir alle aufeinanderfolgenden Zahlen schreiben, beginnend mit der ersten Ziffer der Reihe (in unserem Fall 1) und wir werden den Diagonalen der Raute folgen. Schließlich müssen wir die Zahl „verdoppeln“, damit die Werte der äußeren Zellen auf die entgegengesetzte Seite gehen. Also schneiden sich die äußeren Zellen der vertikalen Achse, dann passiert das Gleiche mit den Zellen der horizontalen Achse, unten sehen Sie ein Beispiel:
Wie löst man magische Quadrate gerader Ordnung?
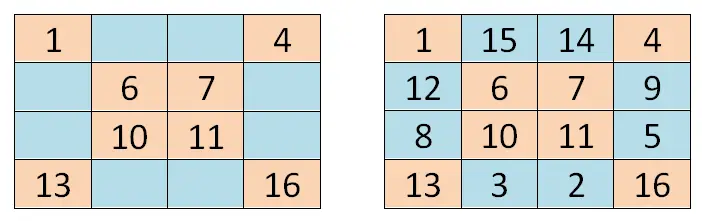
Um ein magisches Quadrat gerader Ordnung (magische Quadrate mit einer geraden Anzahl von Zeilen und Spalten) zu lösen, können wir auf eine Methode zurückgreifen, die sich etwas von der vorherigen unterscheidet, aber ebenfalls auf der Geometrie basiert. Wir beginnen damit, dass wir die erste Zahl der Reihe (in unserem Fall 1) in die obere linke Ecke schreiben. Dann durchlaufen wir die beiden Hauptdiagonalen und schreiben die Werte entsprechend der Position jedes Kästchens.
Sobald wir die beiden Hauptdiagonalen geschrieben haben, müssen wir uns in das erste leere Kästchen setzen, beginnend in der unteren rechten Ecke (in unserem Fall Kästchen 15). Dort schreiben wir den zweiten Wert der Reihe und schreiben die restlichen Werte der Reihe nach (vom kleinsten zum größten), wobei wir die Zellen von rechts nach links und von unten nach oben vervollständigen. Um es klarer zu machen, können Sie sich an dem Bild orientieren, das wir Ihnen unten zeigen:
Wie baut man magische Quadrate?
Um selbst magische Quadrate zu bauen, können wir verschiedene Verfahren befolgen, von denen wir zwei hervorheben möchten. Es ist zu beachten, dass jedes davon zum Erstellen von Quadraten unterschiedlichen Typs verwendet wird. Daher müssen Sie die Methode sorgfältig auswählen, je nachdem, welches Quadrat Sie erstellen möchten:
Siamesische Methode
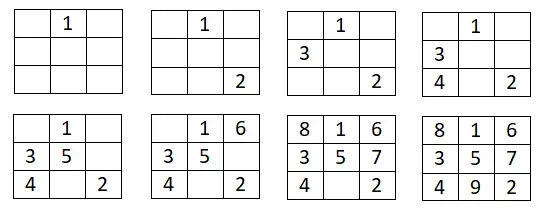
Diese erste Methode ist recht einfach und hilft uns insbesondere dabei , ungerade magische Quadrate jeder Größe zu konstruieren. Das zu befolgende Verfahren ist sehr einfach. Grundsätzlich schreiben wir die erste Zahl der Reihe in das mittlere Feld der ersten Zeile. Von dort aus gehen wir der Reihe nach in der von uns gewählten arithmetischen Folge zurück und schreiben die nächste Zahl nach oben und nach rechts . Liegt diese Position jedoch außerhalb des gezeichneten Quadrats, müssen wir zur letzten Zeile oder Spalte wechseln. Und wenn wir am Ende ein volles Quadrat haben, müssen wir vom letzten Zahlenquadrat, das wir eingegeben haben, ein Quadrat nach unten gehen und machen dann auf die gleiche Weise weiter.
Unten sehen Sie ein Beispiel für 3×3:
Stracheys Methode für magische Quadrate
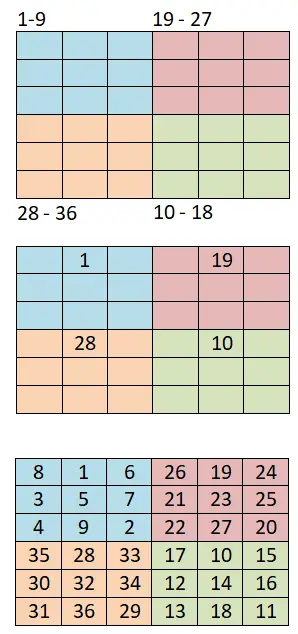
Um magische Quadrate der Ordnung 4k + 2 Paare zu erzeugen, verwenden wir diese andere Methode, die auf der vorherigen Methode (der siamesischen Methode) basiert und ebenfalls sehr einfach ist. Unten sehen Sie die folgenden Schritte und ein Beispiel für ein magisches 6×6-Quadrat:
- In kleinere Quadranten aufteilen: Als Erstes müssen wir das Brett in kleinere Quadrate unterteilen. Wenn wir beispielsweise ein 6×6-Brett haben, müssen wir vier gleiche Quadranten aus 3×3-Quadraten erstellen.
- Verwenden Sie die siamesische Methode: Dann weisen wir jedem kleinen Quadranten einen Zahlenbereich zu. Wenn wir die Sequenz beispielsweise mit 1 beginnen, wären die Bereiche: 1-9 (erster), 10-18 (vierter), 19-27 (zweiter) und 28-36 (dritter).
Conways LUX-Methode für magische Quadrate
Wir werden das letztere System verwenden, wenn wir magische Quadrate der Ordnung 4n + 2 erzeugen wollen, wobei n eine natürliche Zahl ist. Um Quadrate dieses Stils zu erstellen, gehen wir also wie folgt vor:
- Erstellen der Tabelle oder Matrix: Wir beginnen mit der Erstellung einer Matrix vom Grad 2n + 1, wobei n eine natürliche Zahl ist. Damit können wir den Tisch entwerfen, dessen Höhe berücksichtigen und dann mit dem Design beginnen.
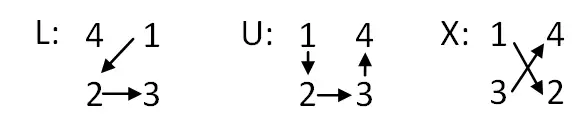
- Positionierung der Buchstaben: Sobald die Tabelle erstellt ist, müssen Sie von oben nach unten schreiben: n + 1 Zeilen von L, 1 Zeile von U und n – 1 Zeilen von X. Und dann müssen Sie das U austauschen in der Mitte mit dem L oben.
- Tauschen Sie Buchstaben gegen Zahlenwerte aus: Jetzt müssen wir die Buchstaben durch Gruppen aus vier aufeinanderfolgenden Zahlen ersetzen. Je nach Buchstabe geben wir den Zahlen die eine oder andere Reihenfolge. Nachfolgend erklärt:
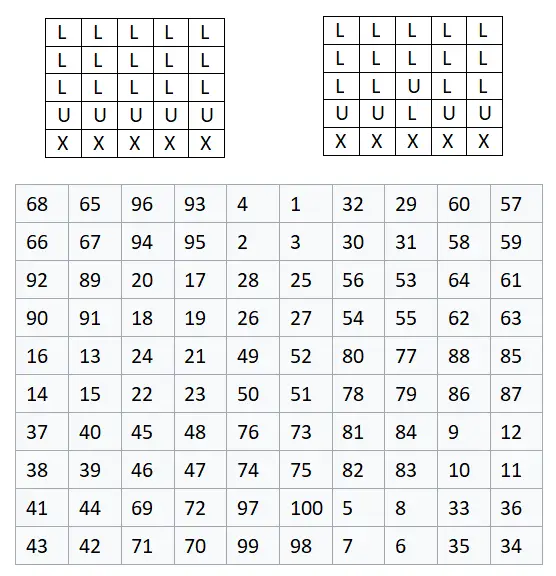
Wir beginnen mit der Konstruktion einer 5×5-Matrix , also n = 2, denn: 2n + 1 = 2 · 2 + 1 = 5. Das bedeutet, dass die Matrix am Ende eine Größe von 10×10 haben wird, weil wir As Wir haben bereits gesagt, dass jede Zelle, die einen Buchstaben enthält, einer Gruppe von vier Zahlen entspricht, also einer 2×2-Matrix. Unten sehen Sie das fertige Beispiel, in dem wir jeden Buchstaben in der im Bild gezeigten Reihenfolge durch eine Gruppe von vier Zahlen ersetzt haben:
Übungen zu magischen Quadraten
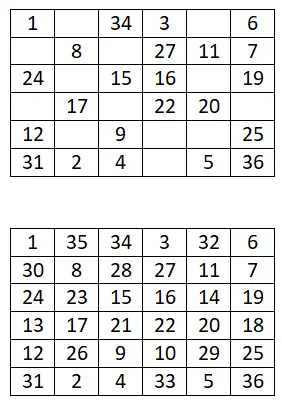
Als nächstes bieten wir Ihnen einige unvollständige magische Quadrate an, die Sie dank der in diesem Artikel erläuterten Konzepte selbst ausfüllen müssen. Denken Sie daran, dass Sie jede der gelehrten Methoden anwenden können. Darüber hinaus müssen Sie berücksichtigen, dass 1 möglicherweise nicht die erste Zahl in der Reihe ist, obwohl sie in die Deklaration aufgenommen wird. Und wenn Sie eine der Übungen beendet haben, können Sie die Lösung unterhalb der Aussage sehen.
3×3 magisches Quadrat
Konstruieren Sie ein magisches 3×3-Quadrat mit nur ungeraden Zahlen:
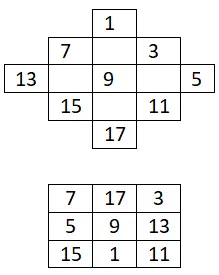
4×4 magisches Quadrat
Vervollständigen Sie das folgende magische 4×4-Quadrat:
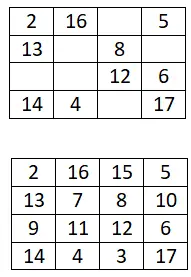
5×5 magisches Quadrat
Vervollständigen Sie das folgende magische 5×5-Quadrat:
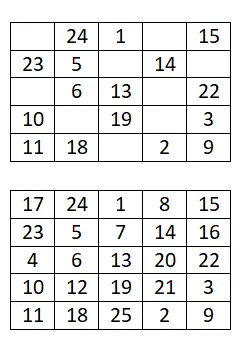
6×6 magisches Quadrat
Vervollständigen Sie das folgende magische 6×6-Quadrat: