Liniengleichungen -

Hier finden Sie die Formeln für alle Arten von Geradengleichungen. Darüber hinaus können Sie Beispiele für deren Berechnung sehen und zusätzlich mit gelösten Übungen zu den Geradengleichungen üben.

Wie lauten alle Gleichungen der Geraden?

Denken Sie daran, dass die mathematische Definition einer Linie eine Menge aufeinanderfolgender Punkte ist, die in derselben Richtung ohne Kurven oder Winkel dargestellt werden.

Um also jede Gerade in der Ebene (im R2) analytisch auszudrücken, verwenden wir die Gleichungen der Geraden, und um sie zu finden, braucht man nur einen Punkt, der zur Geraden gehört, und den Richtungsvektor dieser Geraden. Mit nur diesen beiden geometrischen Elementen können Sie absolut alle verschiedenen Gleichungen der Geraden finden, die wie folgt lauten:

Die Gleichungen der Geraden sind die Vektorgleichung, die parametrischen Gleichungen, die kontinuierliche Gleichung, die implizite (oder allgemeine) Gleichung, die explizite Gleichung, die Punkt-Steigungs-Gleichung und die kanonische (oder segmentale) Gleichung.

Alle Arten von Liniengleichungen haben das gleiche Ziel: eine Linie mathematisch darzustellen. Aber jede Geradengleichung hat ihre eigenen Eigenschaften und daher ist es je nach Problem besser, die eine oder die andere zu verwenden.

Nachdem wir das Konzept der Liniengleichungen kennengelernt haben, gehen wir nun dazu über, die Eigenschaften jedes einzelnen Typs von Liniengleichungen im Besonderen zu analysieren. Unten finden Sie eine detaillierte Erklärung der verschiedenen Arten von Gleichungen in der Zeile. Wenn Sie möchten, können Sie jedoch direkt zum Ende der Übersichtstabelle mit den Formeln aller Gleichungen in der Zeile gehen.

Vektorgleichung der Geraden

$\vv{\text{v}}$

ist der Richtungsvektor der Geraden und

$P$

ein Punkt, der nach rechts gehört:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

Die Formel für die Vektorgleichung der Geraden lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

Gold:

$x$

Und

$y$

sind die kartesischen Koordinaten eines beliebigen Punktes auf der Linie.
$P_1$

Und

$P_2$

sind die Koordinaten eines bekannten Punktes, der Teil der Linie ist

$P(P}_1,P_2).$
$\text{v}_1$

Und

$\text{v}_2$

sind die Komponenten des Richtungsvektors der Geraden

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

ist ein Skalar (eine reelle Zahl), dessen Wert von jedem Punkt auf der Linie abhängt.

Es ist die Vektorgleichung der Geraden in der Ebene, also bei der Arbeit mit Punkten und Vektoren von 2 Koordinaten (im R2). Wenn wir jedoch Berechnungen im Raum (im R3) durchführen würden, müssten wir der Geradengleichung eine zusätzliche Komponente hinzufügen:

$(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)$

Parametrische Gleichungen der Linie

Die parametrischen Gleichungen einer Geraden lassen sich aus ihrer Vektorgleichung ermitteln:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Wir multiplizieren zunächst den Parameter

$t$

durch den Richtungsvektor von rechts:

$(x,y)=(P_1,P_2)+ (t\cdot\text{v}_1,t\cdot\text{v}_2)$

Als nächstes fügen wir die X- und Y-Koordinaten hinzu:

$(x,y)=(P_1+t\cdot\text{v}_1,P_2+t\cdot\text{v}_2)$

Und schließlich, indem wir jede Variable einzeln löschen, erhalten wir die parametrischen Gleichungen der Geraden:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

Gold:

$x$

Und

$y$

sind die kartesischen Koordinaten eines beliebigen Punktes auf der Linie.
$P_1$

Und

$P_2$

sind die Koordinaten eines bekannten Punktes, der Teil der Linie ist

$P(P}_1,P_2).$
$\text{v}_1$

Und

$\text{v}_2$

sind die Komponenten des Richtungsvektors der Geraden

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

ist ein Skalar (eine reelle Zahl), dessen Wert von jedem Punkt auf der Linie abhängt.

Nach wie vor sind dies die parametrischen Gleichungen der Linie in der Ebene (in R2), aber um die parametrischen Gleichungen der Linie im Raum (in R3) zu finden, müsste eine weitere Gleichung für die dritte Variable Z hinzugefügt werden:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}$

Kontinuierliche Gleichung der Geraden

Die kontinuierliche Gleichung jeder Geraden kann aus ihren parametrischen Gleichungen abgeleitet werden:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

Wenn wir die Einstellung löschen

$t$

Aus jeder Parametergleichung erhalten wir die folgenden Ausdrücke:

$t =\cfrac{x-P_1}{\text{v}_1}}$

$t =\cfrac{y-P_2}{\text{v}_2}}$

E Indem wir die beiden resultierenden Gleichungen gleichsetzen, erhalten wir die kontinuierliche Gleichung der Geraden:

$t= t$

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

Kurz gesagt lautet die kontinuierliche Gleichung der Geraden :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

Gold:

$x$

Und

$y$

sind die kartesischen Koordinaten eines beliebigen Punktes auf der Linie.
$P_1$

Und

$P_2$

sind die Koordinaten eines bekannten Punktes, der Teil der Linie ist

$P(P}_1,P_2).$
$\text{v}_1$

Und

$\text{v}_2$

sind die Komponenten des Richtungsvektors der Geraden

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

Diese Formel gilt für die kontinuierliche Gleichung der Linie beim Arbeiten in zwei Dimensionen (in 2D). Wenn wir jedoch Operationen in drei Dimensionen (3D) durchführen würden, müssten wir der Liniengleichung eine zusätzliche Komponente hinzufügen:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}$

Implizite oder allgemeine Gleichung der Geraden

$\vv{\text{v}}$

ist der Richtungsvektor der Geraden und

$P$

ein Punkt, der nach rechts gehört:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

Die Formel für die implizite, allgemeine oder kartesische Gleichung der Geraden lautet:

Gold:

$x$

Und

$y$

sind die kartesischen Koordinaten eines beliebigen Punktes auf der Linie.
der Koeffizient
$A$

ist die zweite Komponente des Richtungsvektors der Geraden:

$A=\text{v}_2}$
der Koeffizient
$B$

ist die erste Komponente des Richtungsvektors mit geändertem Vorzeichen:

$B=-\text{v}_1}$
der Koeffizient
$C$

wird durch Ersetzen des bekannten Punktes berechnet

$P$

in der Geradengleichung.

Die Formel, die implizite Gleichung einer Geraden, kann auch durch Multiplikation der Brüche der stetigen Gleichung erhalten werden.

Explizite Gleichung der Geraden

Die Formel für die explizite Gleichung der Geraden lautet:

Gold:

$m$

ist die Steigung der Geraden.
$n$

sein y-Achsenabschnitt, also die Höhe, in der er die Y-Achse schneidet.

Im folgenden Abschnitt erfahren Sie, wie die Parameter ermittelt werden

$m$

Und

$n$

der Geraden Eine andere Möglichkeit, die explizite Gleichung zu finden, besteht jedoch insbesondere darin, die implizite Gleichung zu verwenden. Dafür muss das Unbekannte gelöst werden

$y$

der impliziten Gleichung.

Bedeutung der Parameter m und n

Wie wir in der Definition der expliziten Gleichung der Geraden gesehen haben, ist der Parameter

$m$

ist die Steigung der Geraden und

$n$

sein y-Achsenabschnitt. Aber was bedeutet das? Sehen wir uns dies anhand der grafischen Darstellung einer Linie an:

Wie lautet die explizite Gleichung der Geraden y=mx+b?

Der Begriff unabhängig

$\bm{n}$

ist der Schnittpunkt der Linie mit der Computerachse (OY-Achse). Zum Beispiel in der Grafik oben

$n$

ist gleich 1, da die Linie die y-Achse bei y=1 schneidet.

Andererseits der Begriff

$\bm{m}$

gibt die Steigung der Geraden an , also ihre Neigung. Wie Sie in der Grafik sehen können,

$m$

ist gleich 2, da die Linie um 2 vertikale Einheiten für 1 horizontale Einheit ansteigt.

Offensichtlich nimmt die Funktion zu, wenn die Steigung positiv ist (steigt), wenn die Steigung negativ ist, nimmt die Funktion ab (sinkt).

Berechnen Sie die Steigung einer Geraden

Sobald wir die Steigung einer Geraden genau kennen, schauen wir uns an, wie sie berechnet wird. Es gibt also drei verschiedene Möglichkeiten, die Steigung einer Geraden numerisch zu bestimmen:

Gegeben seien zwei unterschiedliche Punkte auf der Geraden
$P_1(x_1,y_1)$

Und

$P_2(x_2,y_2),$

Die Steigung der Geraden ist gleich:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Ja
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

ist der Richtungsvektor der Geraden, ihre Steigung ist:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Ja
$\alpha$

ist der Winkel, den die Linie mit der Abszissenachse (X-Achse) bildet, die Steigung der Linie entspricht dem Tangens dieses Winkels:

$m = \text{tg}(\alpha )$

Formel für die explizite Gleichung der Geraden

Punkt-Steigungsgleichung der Geraden

Die Formel für die Punkt-Steigungsgleichung der Geraden lautet:

Gold:

$m$

ist die Steigung der Geraden.
$P_1, P_2$

sind die Koordinaten eines Punktes auf der Geraden

$P(P_1,P_2).$

Kanonische oder segmentale Gleichung der Geraden

Obwohl diese Variante der Geradengleichung weniger bekannt ist, kann die kanonische Geradengleichung aus den Schnittpunkten der Geraden mit den kartesischen Achsen erhalten werden.

Die beiden Schnittpunkte mit den Achsen einer gegebenen Geraden seien:

Mit der X-Achse schneiden:

$(a,0)$

Schnitt mit Y-Achse:

$(0,b)$

Die Formel für die kanonische Geradengleichung lautet:

In der Mathematik wird die kanonische Geradengleichung auch Segmentgleichung oder symmetrische Gleichung genannt.

Andererseits die Koeffizienten

$a$

Und

$b$

Sie können auch aus der allgemeinen Geradengleichung mithilfe der folgenden Formeln ermittelt werden:

$Ax+By+C=0$

$a = -\cfrac{C}{A} \qquad \qquad b = -\cfrac{C}{B}$

Alle Gleichungen der Geraden (Formeln)

Zusammenfassend finden Sie hier eine Tabelle, die die Formeln aller Gleichungen der Geraden zeigt:

Beispiel für die Berechnung von Geradengleichungen

Nachdem wir nun die gesamte Erklärung der Geradengleichung gesehen haben, sehen wir uns an, wie ein typisches Problem von Geradengleichungen gelöst wird:

Finden Sie alle Gleichungen der durch den Punkt bestimmten Geraden
$P$

und der Vektor

$\vv{\text{v}}.$

$P(3,-1) \qquad \qquad \vv{\text{v}}=(2,4)$

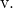
Zunächst finden wir die Vektorgleichung der Geraden aus ihrer Formel:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Setzen Sie einfach die Koordinaten des Punktes und des Vektors in die Formel ein:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(3,-1)+t\cdot (2,4)} \quad \vphantom{\Bigl(}}$

Zweitens finden wir die parametrischen Gleichungen der Geraden durch die entsprechende Formel:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Und wir bestimmen auch die stetige Geradengleichung mit ihrer Formel:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-3}{2}=\cfrac{y-(-1)}{4}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x-3}}{\bm{2}}\bm{=}\cfrac{\bm{y+1}}{\bm{4}}\quad \vphantom{\Biggl(}}$

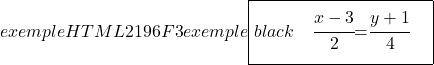
Wie Sie gesehen haben, sind Vektorgleichungen, parametrische und kontinuierliche Gleichungen einfach zu berechnen, Sie müssen lediglich die entsprechenden Formeln verwenden.

Kommen wir nun dazu, die allgemeine (oder implizite) Gleichung der Geraden zu finden. Dazu kreuzen wir die beiden Brüche der stetigen Gleichung:

$4\cdot (x-3)= 2 \cdot (y+1)$

$4x-12= 2y+2$

$4x-12-2y-2=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{4x-2y-14=0}\quad \vphantom{\Bigl(}}$

Jetzt können wir die explizite Gleichung der Geradenlösung für die Unbekannte bestimmen

$y$

der impliziten Gleichung:

$4x-2y-14=0$

$-2y=-4x+14$

$y=\cfrac{-4x+14}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=2x-7}\quad \vphantom{\Bigl(}}$

Daher ist die Steigung der Geraden gleich 2 (Term, der die unabhängige Variable begleitet).

$x$

$m=2$

Und damit können wir die Punkt-Steigungsgleichung der Geraden mit ihrer Formel berechnen:

$y-P_2=m(x-P_1)$

$y-(-1)=2(x-3)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y+1=2(x-3)}\quad \vphantom{\Bigl(}}$

Um schließlich die Segmentgleichung der Geraden zu finden, berechnen wir ihre Schnittpunkte mit den Achsen OX und OY und wenden dann ihre Formel an:

$y=2x-7$

Schnittpunkt mit der Abszissenachse (X-Achse)

$y=0$

$0=2x-7$

$-2x=-7$

$x=\cfrac{-7}{-2} = \cfrac{7}{2}$

$\displaystyle \left(\frac{7}{2}, 0\right)$

Schnittpunkt mit der y-Achse (Y-Achse)

$x=0$

$y=2\cdot 0-7$

$y=-7$

$\displaystyle \left(0,-7\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\frac{\bm{7}}{\bm{2}}}+\cfrac{\bm{y}}{\bm{-7}} \bm{= 1} \quad \vphantom{\Biggl(}}$

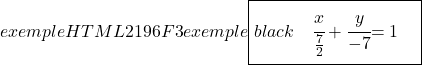
Geradengleichung, die durch zwei Punkte verläuft

Ein weiteres sehr häufiges Problem bei Liniengleichungen besteht darin, die Gleichung der Linie zu finden, die durch zwei gegebene Punkte bestimmt wird. Obwohl wir mit den 2 Punkten und dann der Gleichung den Richtungsvektor der Linie berechnen können, stellen wir Ihnen im Folgenden eine Formel zur Verfügung, mit der Sie direkt und einfach die Gleichung dieser Linie finden können.

Betrachten Sie zwei Punkte, die auf einer Linie liegen:

$P_1(x_1,y_1) \qquad \qquad P_2(x_2,y_2)$

Die Formel zur Ermittlung der Geradengleichung aus ihren beiden Punkten lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1) \end{empheq}$

Mit dieser Formel können wir die Punkt-Steigungsgleichung der Geraden direkt berechnen, wenn wir zwei Punkte erhalten, durch die die Gerade verläuft.

Probleme mit Geradengleichungen gelöst

Übung 1

Finden Sie die Vektorgleichung, die parametrischen Gleichungen und die kontinuierliche Gleichung der durch den Punkt definierten Linie

$P$

und sein Richtungsvektor

$\vv{\text{v}}.$

Sei beides:

$P(0,3) \qquad \qquad \vv{\text{v}}=(-1,5)$

siehe Lösung

Zuerst berechnen wir die Vektorgleichung der Geraden aus ihrer Formel:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(0,3)+t\cdot (-1,5)} \quad \vphantom{\Bigl(}}$

Anschließend ermitteln wir die parametrischen Gleichungen der Geraden mithilfe der entsprechenden Formel:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Und schließlich bestimmen wir die stetige Geradengleichung mit der zugehörigen Formel:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-0}{-1}=\cfrac{y-3}{5}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x}}{\bm{-1}}\bm{=}\cfrac{\bm{y-3}}{\bm{5}}\quad \vphantom{\Biggl(}}$

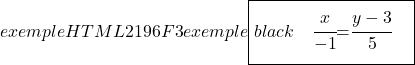
Übung 2

Finden Sie die implizite Gleichung, die explizite Gleichung und die Punkt-Steigungsgleichung der durch den Punkt bestimmten Linie

$P$

und sein Richtungsvektor ist

$\vv{\text{v}}.$

$P(-4,3) \qquad \qquad \vv{\text{v}}=(2,6)$

siehe Lösung

Die Formel für die implizite Gleichung der Geraden lautet:

$Ax+By+C=0$

Wir müssen also die Koeffizienten A, B und C finden. Die Unbekannten A und B erhält man aus den Koordinaten des Richtungsvektors der Geraden, weil die folgende Gleichheit immer verifiziert ist:

$\vv{\text{v}}= (-B,A)$

Folglich ist der Koeffizient A die zweite Koordinate des Vektors und der Koeffizient B ist die erste Koordinate des Vektors mit geändertem Vorzeichen:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}$

Daher müssen wir nur den Koeffizienten C ermitteln. Dazu müssen wir den Punkt, von dem wir wissen, dass er zur Geraden gehört, in deren Gleichung einsetzen:

$P(-4,3)$

$6x-2y+C=0 \ \xrightarrow{x=-4 \ ; \ y=3} \ 6\cdot (-4)-2\cdot 3+C=0$

$-24-6+C=0$

$-30+C=0$

$C=30$

Die implizite, allgemeine oder kartesische Gleichung der Geraden lautet also:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x-2y+30=0}\quad \vphantom{\Bigl(}}$

Jetzt können wir die explizite Gleichung der Geradenlösung für die Unbekannte bestimmen

$y$

der impliziten Gleichung:

$6x-2y+30=0$

$-2y=-6x-30$

$y=\cfrac{-6x-30}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=3x+15}\quad \vphantom{\Bigl(}}$

Daher ist die Steigung der Geraden gleich 3 (Term vor der unabhängigen Variablen).

$x$

$m=3$

Und aus dem Wert der Steigung der Geraden können wir die Punkt-Steigungsgleichung der Geraden mit ihrer Formel berechnen:

$y-P_2=m(x-P_1)$

$y-3=3(x-(-4))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-3=3(x+4)}\quad \vphantom{\Bigl(}}$

Übung 3

Bestimmen Sie 3 Punkte auf der folgenden Linie, ausgedrückt als implizite oder allgemeine Gleichung:

$4x+2y-8 = 0$

siehe Lösung

Um einen Punkt auf einer Linie zu berechnen, müssen wir lediglich einer der Variablen einen Wert zuweisen und dann den Wert der anderen Variablen an diesem Punkt ermitteln.

Wir berechnen einen ersten Punkt indem wir tun

$x=0:$

$4\cdot 0+2y-8 = 0$

$2y = 8$

$y = \cfrac{8}{2}$

$y = 4$

$\bm{P_1(0,4)}$

Dann finden wir einen zweiten Punkt, der der Variablen einen anderen Wert gibt

$x,$

Zum Beispiel

$x=1:$

$4\cdot 1+2y-8 = 0$

$2y = 8-4$

$2y = 4$

$y = \cfrac{4}{2}$

$y = 2$

$\bm{P_2(1,2)}$

Und schließlich berechnen wir durch Lösen einen dritten Punkt

$x=2:$

$4\cdot 2+2y-8 = 0$

$2y = 8-8$

$2y = 0$

$y = \cfrac{0}{2}$

$y = 0$

$\bm{P_3(2,0)}$

Übung 4

Finden Sie alle Gleichungen der durch den Punkt definierten Linie

$P$

und der Vektor

$\vv{\text{v}}.$

$P(-1,4) \qquad \qquad \vv{\text{v}}=(-3,6)$

siehe Lösung

Zunächst finden wir die Vektorgleichung der Geraden aus ihrer Formel:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(-1,4)+t\cdot (-3,6)} \quad \vphantom{\Bigl(}}$

Zweitens finden wir die parametrischen Gleichungen der Geraden durch die entsprechende Formel:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Und wir bestimmen auch die kontinuierliche Gleichung der Geraden anhand ihrer Formel:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{-3}=\cfrac{y-4}{6}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x+1}}{\bm{-3}}\bm{=}\cfrac{\bm{y-4}}{\bm{6}}\quad \vphantom{\Biggl(}}$

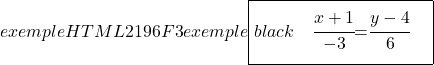
Kommen wir nun dazu, die implizite oder allgemeine Gleichung der Geraden zu finden. Dazu kreuzen wir die beiden Brüche der stetigen Gleichung:

$6\cdot (x+1)= -3 \cdot (y-4)$

$6x+6= -3y+12$

$6x+6+3y-12=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x+3y-6=0}\quad \vphantom{\Bigl(}}$

Jetzt können wir die explizite Gleichung der Geradenlösung für die Unbekannte bestimmen

$y$

der impliziten Gleichung:

$6x+3y-6=0$

$3y=-6x+6$

$y=\cfrac{-6x+6}{3}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=-2x+2}\quad \vphantom{\Bigl(}}$

Daher entspricht die Steigung der Linie -2 (Term, der die unabhängige Variable begleitet).

$x$

$m=-2$

Und damit können wir die Punkt-Steigungsgleichung der Geraden mit ihrer Formel berechnen:

$y-P_2=m(x-P_1)$

$y-4=-2(x-(-1))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-4=-2(x+1)}\quad \vphantom{\Bigl(}}$

Um schließlich die Segmentgleichung der Geraden zu finden, berechnen wir die Schnittpunkte der Geraden mit den Achsen OX und OY und verwenden dann ihre Formel:

$y=-2x+2$

Schnittpunkt mit der Abszissenachse (X-Achse)

$y=0$

$0=-2x+2$

$2x=2$

$x=\cfrac{2}{2} =1$

$\displaystyle \left(1, 0\right)$

Schnittpunkt mit der y-Achse (Y-Achse)

$x=0$

$y=-2\cdot 0+2$

$y=2$

$\displaystyle \left(0,2\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\bm{1}}+\cfrac{\bm{y}}{\bm{2}} \bm{= 1} \quad \vphantom{\Biggl(}}$

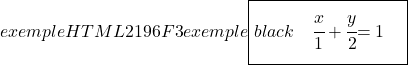
Übung 5

Finden Sie die Gleichung der Geraden, die durch die folgenden zwei Punkte verläuft:

$P_1 (4,-1) \qquad \qquad P_2(5,2)$

siehe Lösung

Da wir bereits zwei Punkte auf der Geraden kennen, wenden wir die Formel für die Geradengleichung direkt auf 2 gegebene Punkte an:

$y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1)$

Jetzt setzen wir die kartesischen Koordinaten der Punkte in die Formel ein:

$y-(-1)= \cfrac{2-(-1)}{5-4} (x-4)$

Und schließlich berechnen wir die Steigung der Geraden:

$y+1= \cfrac{3}{1} (x-4)$

$y+1= 3(x-4)$

Die Gleichung der Geraden, die durch diese beiden Punkte geht, lautet daher:

$\bm{y+1= 3(x-4)}$

Wie lauten alle Gleichungen der Geraden?

Vektorgleichung der Geraden

Parametrische Gleichungen der Linie

Kontinuierliche Gleichung der Geraden

Implizite oder allgemeine Gleichung der Geraden

Explizite Gleichung der Geraden

Bedeutung der Parameter m und n

Berechnen Sie die Steigung einer Geraden

Punkt-Steigungsgleichung der Geraden

Kanonische oder segmentale Gleichung der Geraden

Alle Gleichungen der Geraden (Formeln)

Beispiel für die Berechnung von Geradengleichungen

Geradengleichung, die durch zwei Punkte verläuft

Probleme mit Geradengleichungen gelöst

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Kommentar verfassen Kommentieren abbrechen