Lineare Funktion und affine Funktion -

In diesem Artikel finden Sie die Erklärung der affinen Funktion und der linearen Funktion sowie die Unterschiede zwischen diesen beiden Funktionstypen. Darüber hinaus sehen Sie Beispiele für die grafische Darstellung einer affinen Funktion und einer linearen Funktion sowie für die Berechnung ihrer Ausdrücke aus zwei Punkten. Schließlich können Sie mit mehreren Schritt-für-Schritt-Übungen trainieren.

Was ist eine affine Funktion und eine lineare Funktion?

Die Definitionen der affinen Funktion und der linearen Funktion lauten wie folgt:

Eine affine Funktion ist eine Polynomfunktion ersten Grades, also eine Funktion, die im Diagramm dargestellt eine Gerade ist. Die zugehörigen Funktionen sind wie folgt:

$f(x)=mx+n$

Gold

$m$

ist die Steigung der Geraden und

$n$

Dies ist der y-Achsenabschnitt, d. h. der Schnittpunkt der Funktion mit der vertikalen Achse.

In der Mathematik werden affine Funktionen im Kontext der linearen Algebra auch lineare Transformationen genannt.

Eine lineare Funktion ist eine affine Funktion, die keinen unabhängigen Term hat. Daher lautet die Formel für lineare Funktionen:

$f(x)=mx$

Gold

$m$

ist die Steigung der Geraden.

Der Definitionsbereich und der Bereich (oder Bereich) der linearen Funktion und der affinen Funktion sind alle reelle Zahlen:

$\text{Dom } f=\mathbff{R}$

$\text{Im } f= \mathbb{R}$

Was ist der Unterschied zwischen einer linearen Funktion und einer affinen Funktion?

Nachdem Sie nun die Konzepte der linearen Funktion und der affinen Funktion kennengelernt haben, wird Ihnen aufgefallen sein, dass sie einander sehr ähnlich sind. Der folgende Unterschied zwischen ihnen ist jedoch sehr wichtig:

Der einzige Unterschied zwischen der linearen Funktion und der affinen Funktion besteht darin, dass die lineare Funktion keinen unabhängigen Term hat, während bei der affinen Funktion immer der Koeffizient des Achsenabschnitts (n) ungleich Null (0) ist.

Lineare Funktion

$f(x)=mx$

lineare Funktion

$f(x)=mx+n$

Dies impliziert, dass eine lineare Funktion immer durch den Koordinatenursprung, den Punkt (0,0), verläuft . Andererseits wird eine affine Funktion diesen Punkt niemals durchlaufen, da sie einen anderen Achsenabschnitt als 0 hat.

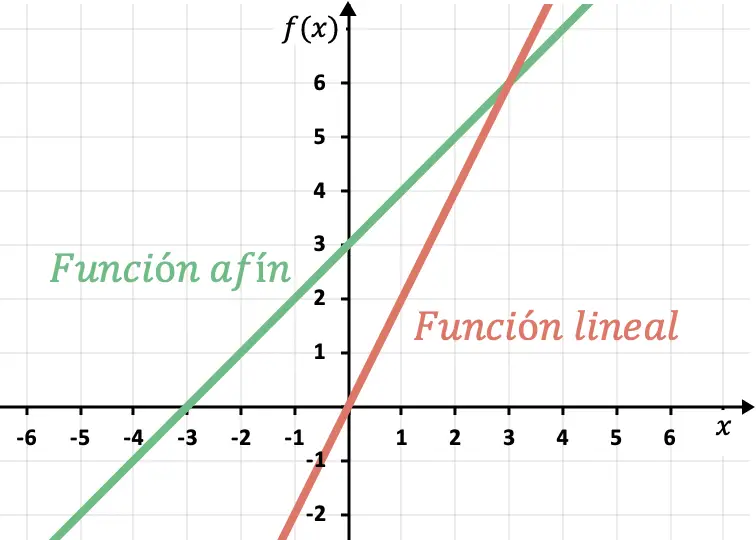
Was ist der Unterschied zwischen einer linearen Funktion und einer affinen Funktion?

Steigung und y-Achsenabschnitt einer linearen oder affinen Funktion

In diesem Abschnitt analysieren wir ein Beispiel einer affinen oder linearen Funktion, um die Bedeutung der Begriffe zu verstehen

$m$

Und

$n$

, oder mit anderen Worten, die Steigung und der y-Achsenabschnitt.

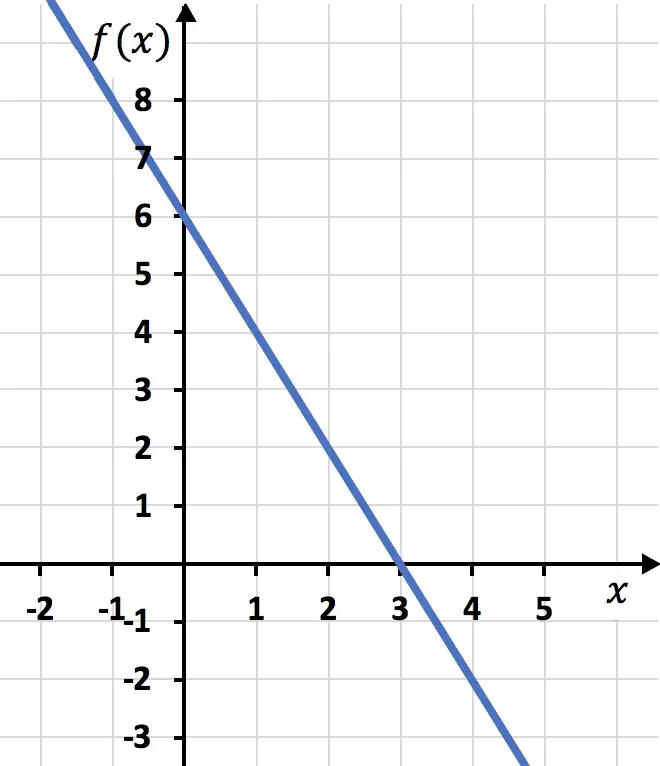
Bestimmen Sie den Ausdruck für die im Diagramm dargestellte Funktion und klassifizieren Sie ihn als lineare oder affine Funktion.

Diese Funktionstypen folgen dem folgenden Ausdruck:

$f(x)=mx+n$

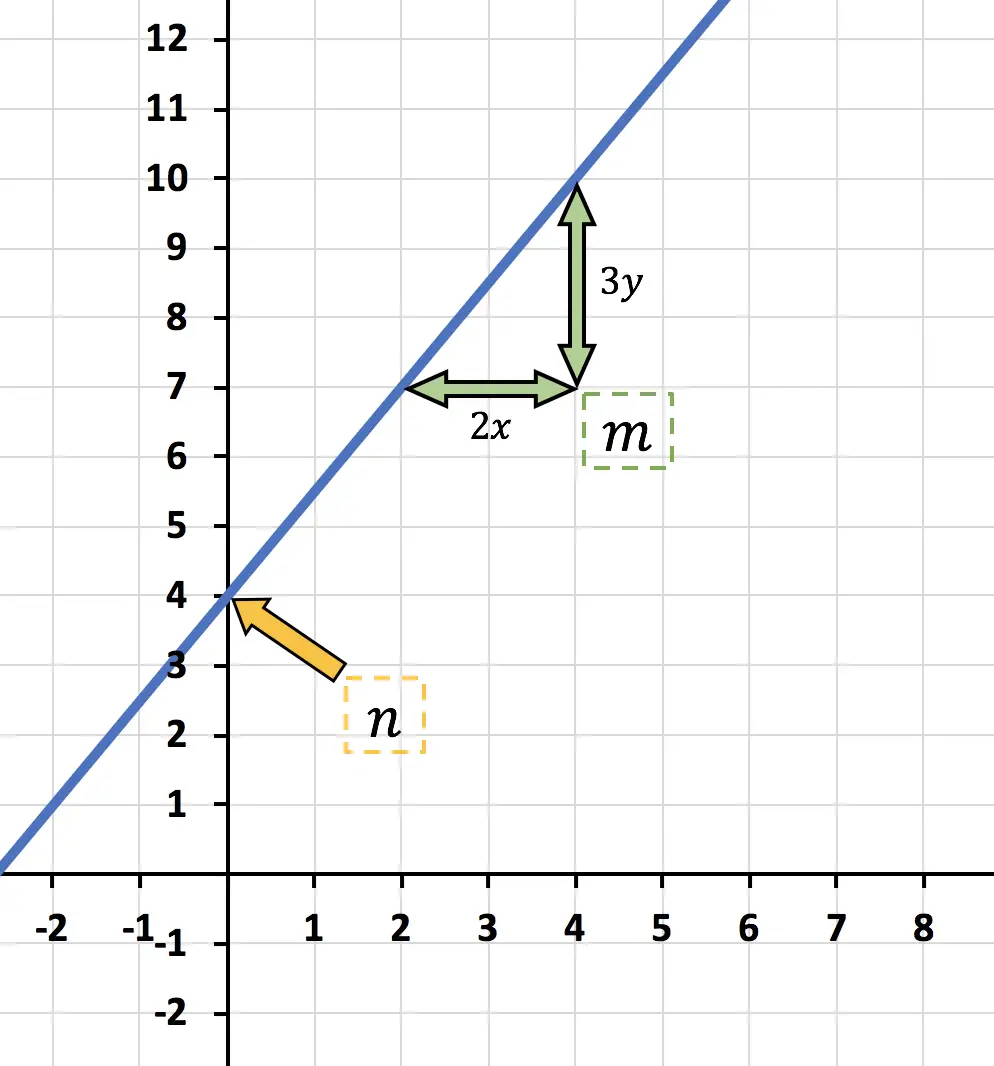
Bedeutung: Steigung und y-Achsenabschnitt der linearen oder affinen Funktion m und n

$n$

Dies ist der Y-Achsenabschnitt, dh der Schnittpunkt der Funktion mit der vertikalen Y-Achse. Also in diesem Fall:

$n=4$

Auf einer anderen Seite,

$m$

ist die Steigung der Geraden. Y kann berechnet werden, indem man die Differenz von y zwischen zwei Punkten durch die Differenz von x zwischen diesen beiden Punkten dividiert:

$m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}$

$m$

sagt „um wie viel y für jedes x zunimmt“ , also in diesem Fall die Funktion „3y erhöht sich für jedes 2x“ .

Zusammenfassend lautet der Ausdruck für die im Diagramm dargestellte affine Funktion:

$\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}$

Da der y-Achsenabschnitt außerdem ungleich Null ist, handelt es sich um eine affine Funktion .

Nachfolgend zeigen wir Ihnen weitere Beispiele für lineare und affine Funktionen, um Ihr Verständnis zu vervollständigen:

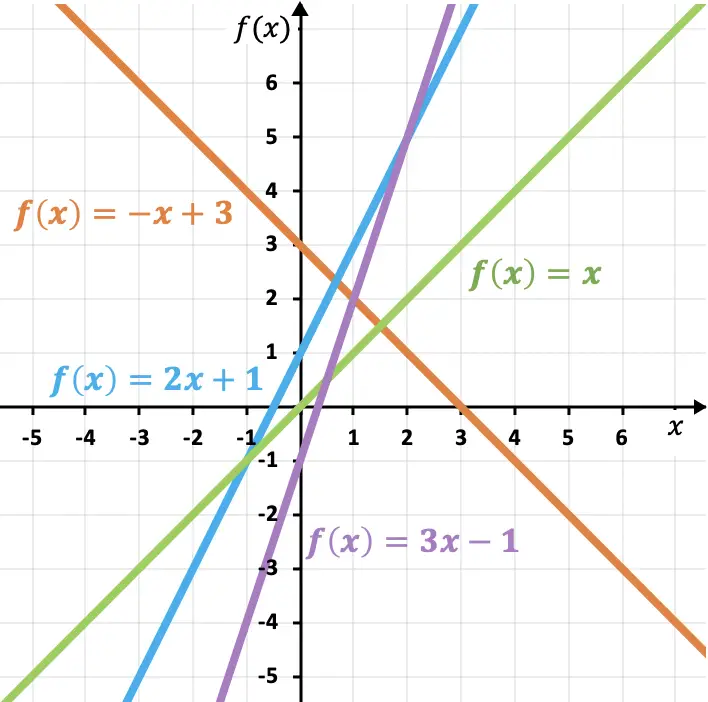
Wie Sie in diesen Beispielen sehen können, gilt: Je größer die Steigung, desto steiler die Linie und desto größer die Funktion. Ebenso bestimmt der Steigungskoeffizient das Wachstum oder die Abnahme einer Funktion:

Wenn die Steigung positiv ist, ist die Funktion steigend , das heißt, sie nimmt mit zunehmendem x zu.
Wenn die Steigung negativ ist, ist die Funktion fallend , das heißt, sie nimmt mit zunehmendem x ab.

Darüber hinaus können Sie anhand ihrer Steigungen erkennen, ob zwei Geraden parallel oder senkrecht sind:

Wenn zwei Geraden die gleiche Steigung haben, sind sie parallel , das heißt, sie schneiden sich an keinem Punkt oder sind völlig identisch.

$m_1 = m_2$

Andererseits sind zwei Geraden senkrecht , d. h. sie schneiden sich in einem vertikalen Winkel (90°), wenn ihre Steigungen der folgenden Beziehung entsprechen:

$m_1 = -\cfrac{1}{m_2}$

Beispiel für die Darstellung einer affinen oder linearen Funktion

Sehen wir uns anhand eines Beispiels an, wie man eine Funktion ersten Grades grafisch darstellt.

Stellen Sie die folgende affine Funktion grafisch dar:

$f(x)=2x-1$

Als Erstes müssen wir ein Array von Werten erstellen. Dazu gewähren wir die Werte, die wir wollen

$x$

um Werte von zu erhalten

$f(x)$

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

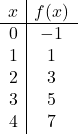
Obwohl eine Wertetabelle mit zwei Punkten ausreichend ist, können wir mehr Punkte tun, um sicherzustellen, dass sie korrekt ist.

Nachdem wir die Wertetabelle erstellt haben, tragen wir die Punkte in die Grafik ein:

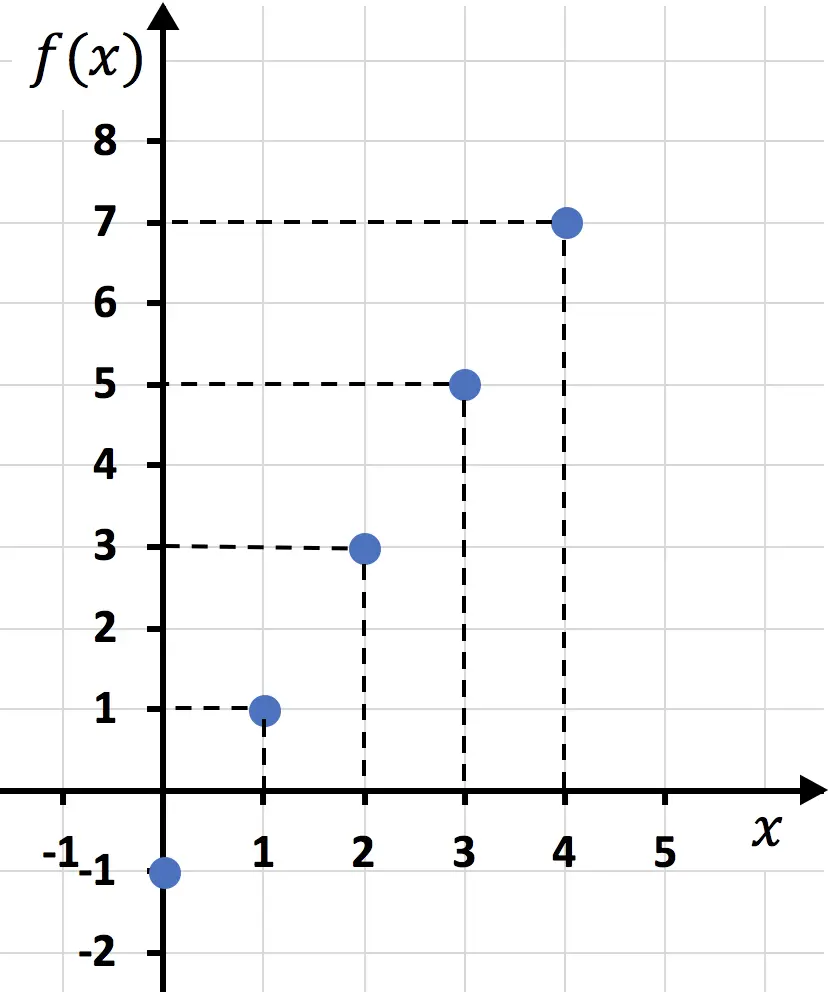
wie man eine Linie oder eine lineare Funktion darstellt oder und affin

Und zum Schluss fügen wir die Punkte zusammen und ziehen eine Linie:

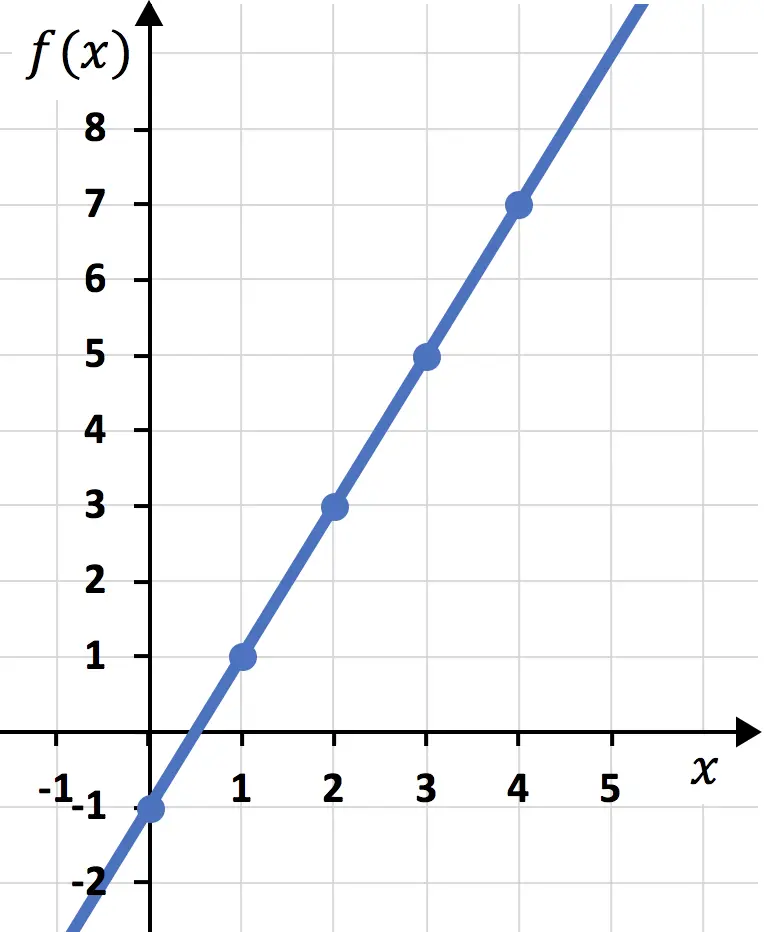
grafische Darstellung einer linearen oder affinen Funktion

Und auf diese Weise haben wir die Funktion bereits in einem Diagramm dargestellt. Wie Sie sehen, ist es nicht kompliziert. Sie müssen lediglich zunächst eine Wertetabelle erstellen und dann die Punkte in einem Diagramm darstellen.

So berechnen Sie eine lineare oder affine Funktion aus zwei Punkten

Sehen wir uns nun anhand eines Beispiels an, wie man aus zwei Punkten eine lineare oder affine Funktion findet:

Berechnen Sie die lineare Funktion, die erfüllt
$f(3)=5$

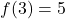
und gehen Sie den Punkt durch

$(1,-1).$

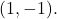
Erstens,

$f(3)=5$

Das bedeutet, dass die Funktion durch den Punkt verläuft

$(3,5)$

Da wir also zwei Punkte haben, durch die die Funktion verläuft, können wir die Steigung berechnen

$m$

Funktion:

Betrachtet man zwei Punkte,

$P_1=(x_1,y_1)$

Und

$P_2=(x_2,y_2)$

, Neigung

$m$

der Funktion wird berechnet:

$m=\cfrac{y_2-y_1}{x_2-x_1}$

In unserem Fall verläuft die Funktion durch die Punkte

$(3,5)$

Und

$(1,-1)$

. Also die Steigung

$m$

der Funktion ist:

$m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3$

Die Funktion hat daher die Form:

$f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n$

Sobald wir es wissen

$m$

Wir können das Rätsel lösen

$n$

. Dazu setzen wir die Koordinaten eines zur Funktion gehörenden Punktes in die Gleichung ein. Zum Beispiel Punkt (3.5):

$f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n$

Wir lösen die resultierende Gleichung:

$5=3\cdot 3+n$

$5= 9 + n$

$5-9=n$

$-4=n$

Die lineare Funktion ist daher:

$\bm{f(x)=3x-4}$

Aufgaben zu linearen und affinen Funktionen gelöst

Übung 1

Bestimmen Sie die Steigung und den Ursprung der folgenden affinen Funktion:

$f(x)=-5x-2$

Sehen Sie sich die Lösung an

Eine lineare Funktion hat die Form

$f(x)=mx+n .$

Die Steigung der Funktion ist daher die Zahl, die x begleitet, in diesem Fall -5:

$\bm{m=-5}$

Und der y-Achsenabschnitt ist der unabhängige Term, der in diesem Fall -2 ist:

$\bm{n=-2}$

Übung 2

Stellen Sie die folgende affine Funktion grafisch dar:

$f(x)=x+1$

Sehen Sie sich die Lösung an

Wir geben zunächst Werte an

$x$

So erstellen Sie die Wertetabelle:

$x= 0 \ \longrightarrow \ f(0)=0+1 = 1$

$x= 1 \ \longrightarrow \ f(1)=1+1= 2$

$x= 2 \ \longrightarrow \ f(2)=2+1 = 3$

$x= 3 \ \longrightarrow \ f(3)=3+1 = 4$

$x= 4 \ \longrightarrow \ f(4)=4+1 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}$

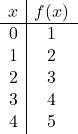
Und dann stellen wir die Punkte aus der Wertetabelle in der Grafik dar und zeichnen die Linie:

Beispiel einer linearen oder affinen Funktion

Übung 3

Zeichnen Sie die folgende affine Funktion in das Diagramm ein:

$f(x)=-2x+6$

Sehen Sie sich die Lösung an

Wir geben zunächst Werte an

$x$

So erstellen Sie die Wertetabelle:

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6$

$x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4$

$x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2$

$x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0$

$x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}$

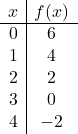
Und schließlich stellen wir die Punkte aus der Wertetabelle in der Grafik dar und zeichnen die Linie:

Übung Schritt für Schritt der linearen und affinen Funktion gelöst

Übung 4

Finden Sie den Ausdruck für die affine Funktion, die durch die Punkte (2,3) und (0,1) verläuft.

Sehen Sie sich die Lösung an

Die Funktion verläuft durch die Punkte (2,3) und (0,1), daher ist die Steigung der Funktion:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1$

Und die Funktion wird die Form haben:

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

Sobald wir m kennen, können wir n berechnen. Dazu müssen wir die Koordinaten eines zur Funktion gehörenden Punktes in die Gleichung einsetzen. Zum Beispiel Punkt (2,3):

$f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}$

$3=2+n$

Wir müssen nun die resultierende Gleichung lösen:

$3-2=n$

$1 = n$

Die Funktion entspricht daher dem folgenden Ausdruck:

$\bm{f(x)=x+1}$

Übung 5

Stellen Sie die folgende affine Funktion grafisch dar:

$f(x)=2x-1$

Sehen Sie sich die Lösung an

Wir geben zunächst Werte an

$x$

So erstellen Sie die Wertetabelle:

$x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

Und dann stellen wir die Punkte aus der Wertetabelle in der Grafik dar und zeichnen die Linie:

Gelöste Übungen zur grafischen Darstellung einer linearen oder affinen Funktion

Übung 6

Berechnen Sie die lineare Funktion, die die folgenden zwei Bedingungen erfüllt:

$\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}$

Sehen Sie sich die Lösung an

Möge es wahr werden

$f(3)=-2$

Das bedeutet, dass die Funktion durch den Punkt (3,-2) verläuft. Und auf die gleiche Weise

$f(-1)=6$

Das bedeutet, dass die Funktion durch den Punkt (-1,6) verläuft.

Die Funktion verläuft also durch die Punkte (3,-2) und (-1,6), daher ist ihre Steigung:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2$

Die Funktion hat daher die Form:

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

Und sobald wir m kennen, können wir n berechnen. Dazu setzen wir die Koordinaten eines Punktes, der zur Funktion gehört, in die Gleichung ein. Zum Beispiel der Punkt (3,-2):

$f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n$

Und wir lösen die resultierende Gleichung:

$-2=-6+n$

$-2+6=n$

$4 = n$

Die Funktion lautet also:

$\bm{f(x)=-2x+4}$

Übung 7

Finden Sie die affine Funktion, die es ausführt

$f(1) =6$

und geht durch den Punkt (3.5).

Sehen Sie sich die Lösung an

Möge es wahr werden

$f(1)=6$

Das bedeutet, dass die Funktion durch den Punkt (1,6) verläuft.

Die Funktion verläuft also durch die Punkte (1.6) und (3.5) und ihre Steigung ist daher:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}$

Die Funktion hat daher die Form:

$\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n$

Sobald wir den Term m kennen, können wir den Koeffizienten n berechnen. Dazu setzen wir die Koordinaten eines Punktes, der zur Funktion gehört, in die Gleichung ein. Zum Beispiel der Punkt (1,6):

$\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n$

Wir lösen die resultierende Gleichung:

$6=-\cfrac{1}{2}+n$

$6+\cfrac{1}{2}=n$

Denken Sie daran, dass Sie zum Addieren von Brüchen diese zunächst auf einen gemeinsamen Nenner reduzieren und dann die Zähler addieren müssen:

$\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n$

$\cfrac{12}{2} +\cfrac{1}{2}=n$

$\cfrac{13}{2}=n$

Die Funktion lautet also:

$\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}$

Übung 8

Lösen Sie das folgende Problem im Zusammenhang mit linearen und affinen Funktionen:

Ein Geschäft verkauft 40 Einheiten eines Produkts, wenn der Preis 15 €/Einheit beträgt, und 65 Einheiten, wenn der Preis 10 €/Einheit beträgt.

Berechnen Sie die Nachfragefunktion für das Produkt unter der Annahme, dass es sich um eine affine Funktion handelt.
Wie viele Einheiten werden verkauft, wenn der Preis auf 12 €/Einheit festgelegt ist?

Sehen Sie sich die Lösung an

Da es sich um eine affine Funktion handelt, ist die Funktion vom Typ

$f(x)=mx+n .$

Gold

$x$

wird der Stückpreis des Produkts sein und

$f(x)$

werden die verkauften Einheiten sein.

In der Pressemitteilung heißt es, dass bei einem Preis von 15 €/Stück 40 Stück verkauft werden. Daher als

$x$

ist der Preis und

$f(x)$

Bei verkauften Einheiten muss folgende Gleichheit beachtet werden:

$f(15)=40$

Und wenn der Preis 10 €/Einheit beträgt, werden 65 Einheiten verkauft. Also mit der gleichen Argumentation:

$f(10)=65$

Möge es wahr werden

$f(15)=40$

Das bedeutet, dass die Funktion durch den Punkt (15.40) verläuft. UND

$f(10)=65$

Das bedeutet, dass die Funktion durch den Punkt (10.65) verläuft.

Die Steigung der Funktion ist daher:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5$

Die Funktion hat daher die Form:

$f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n$

Sobald wir m kennen, können wir n berechnen. Dazu setzen wir die Koordinaten eines Punktes, der zur Funktion gehört, in die Gleichung ein. Zum Beispiel der Punkt (15:40 Uhr):

$f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n$