▷ Berechnen Sie das Kreuzprodukt zweier Vektoren (Beispiele)

Auf dieser Seite wird erklärt, was das Kreuzprodukt zweier Vektoren ist und wie es berechnet wird. Außerdem erfahren Sie, wie Sie mithilfe der rechten Handregel (oder des Korkenziehers) die Richtung und Richtung des Kreuzprodukts ermitteln. Darüber hinaus finden Sie die Einsatzmöglichkeiten dieser Art von Bedienung sowie Beispiele, Übungen und Schritt für Schritt gelöste Probleme.

Was ist das Kreuzprodukt zweier Vektoren?

In der Mathematik ist das Kreuzprodukt eine Operation zwischen zwei Vektoren im dreidimensionalen Raum (im R3). Das Ergebnis dieser Vektoroperation ist ein Vektor mit einer Richtung senkrecht zu den beiden multiplizierten Vektoren und einem Modul, der dem Produkt der Module der Multiplikatorvektoren mit dem Sinus des Winkels, den sie bilden, entspricht. Mit anderen Worten, seine Formel lautet:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

Wie Sie in der vorherigen Formel sehen, wird das Kreuzprodukt bezeichnet

$\bm{\times}$

, weshalb es auch Kreuzprodukt genannt wird. Es wird manchmal auch das Gibbs-Vektorprodukt genannt, da es von ihm erfunden wurde.

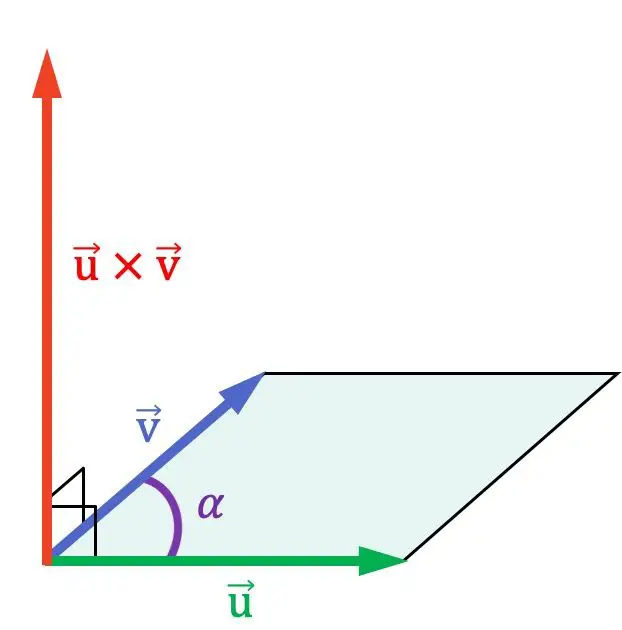
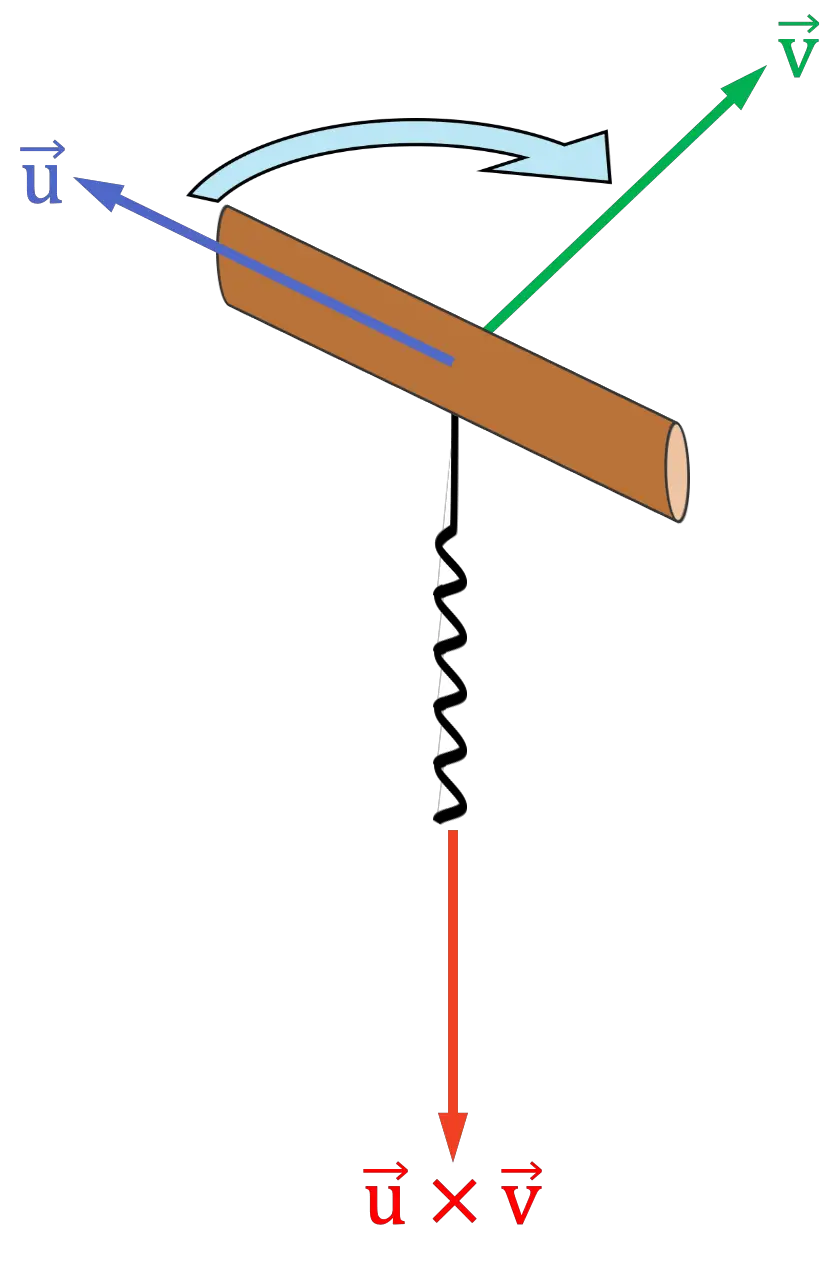
Wie Sie in der vorherigen grafischen Darstellung sehen können, steht das Kreuzprodukt senkrecht auf den beiden Vektoren, die sie multiplizieren, und ist daher normal auf der Ebene, die sie enthält.

Formel zur Berechnung des Kreuzprodukts zweier Vektoren

Wenn wir die kartesischen Koordinaten der Vektoren kennen, können wir ihr Kreuzprodukt am einfachsten berechnen, indem wir nach einer 3×3-Determinante auflösen. Sehen Sie, wie es gemacht wird:

Betrachten Sie zwei beliebige Vektoren:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Sein Vektorprodukt ist:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

Wo die Vektoren

$\vv{i}, \vv{j},\vv{k}$

Dies sind die Einheitsvektoren in der X-, Y- und Z-Achsenrichtung.

Sehen wir uns ein Beispiel für die Berechnung des Kreuzprodukts zwischen zwei Vektoren an:

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

Um das Vektorprodukt zwischen den Vektoren zu bestimmen, müssen wir die folgende Determinante der Ordnung 3 ermitteln:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

In diesem Fall lösen wir die Determinante durch Adjuvantien oder Cofaktoren (es könnte auch die Sarrus-Regel verwendet werden):

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

Das Ergebnis des Vektorprodukts der beiden Vektoren ist daher:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

Bestimmt die Richtung und Richtung des Kreuzprodukts

Manchmal müssen wir die Komponenten des aus dem Kreuzprodukt resultierenden Vektors nicht kennen, aber es reicht aus, seinen Modul, seine Richtung und seine Richtung zu finden. Dies geschieht häufig in der Physik, insbesondere bei der Berechnung von Kräften.

So gibt es mehrere Regeln zum Ermitteln der Richtung und Richtung des Vektorprodukts, die bekanntesten sind die Rechte-Hand-Regel , entweder mit drei Fingern oder mit der ganzen Hand, und die Korkenzieher-Regel (oder die Schraube) . Sie können jede davon verwenden, müssen also nicht alle kennen. Wir erklären Ihnen trotzdem die drei Regeln, damit Sie bei der bleiben können, die Ihnen am besten gefällt. 😉

Regel der rechten Hand (3 Finger)

Die 3-Finger-Version der Regel oder des Gesetzes der rechten Hand umfasst die Durchführung der folgenden Schritte:

Platzieren Sie den Zeigefinger Ihrer rechten Hand in Richtung des ersten Vektors des Kreuzprodukts
$(\vv{\text{u}}).$
Platzieren Sie den Mittelfinger (oder Mittelfinger) Ihrer rechten Hand in Richtung des zweiten Vektors des Kreuzprodukts
$(\vv{\text{v}}).$
Die resultierende Daumenposition gibt die Richtung und Richtung des Kreuzprodukts an
$(\vv{\text{u}}\times\vv{\text{v}}).$

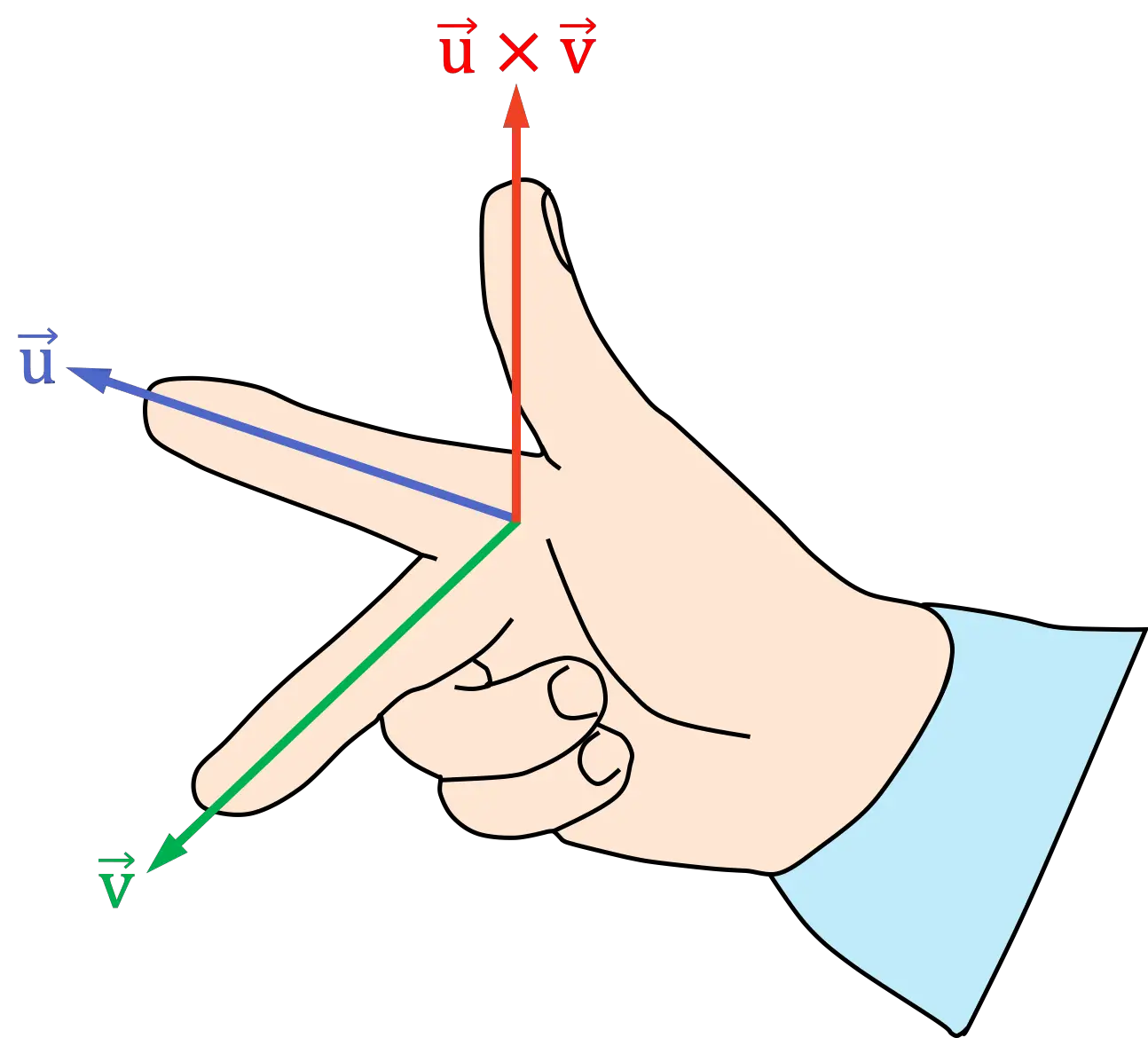
Regel der rechten Hand (Handfläche)

Die Palmar-Version der Regel oder des Gesetzes für die rechte Hand ist der vorherigen Regel sehr ähnlich. Um es anzuwenden, müssen Sie die folgenden Schritte ausführen:

Legen Sie Ihre rechte Hand so hin, dass Ihre Finger in die gleiche Richtung wie der erste Vektor des Kreuzprodukts zeigen
$(\vv{\text{u}}).$
Schließen Sie Ihre rechte Hand, indem Sie Ihre Finger in Richtung des zweiten Vektors des Kreuzprodukts bewegen
$(\vv{\text{v}}).$

Sie müssen Ihre Hand auf der Seite schließen, auf der der Winkel (oder Abstand) zwischen den Vektoren kleiner ist.
Die resultierende Position des Daumens bestimmt die Richtung des Kreuzprodukts
$(\vv{\text{u}}\times\vv{\text{v}}).$

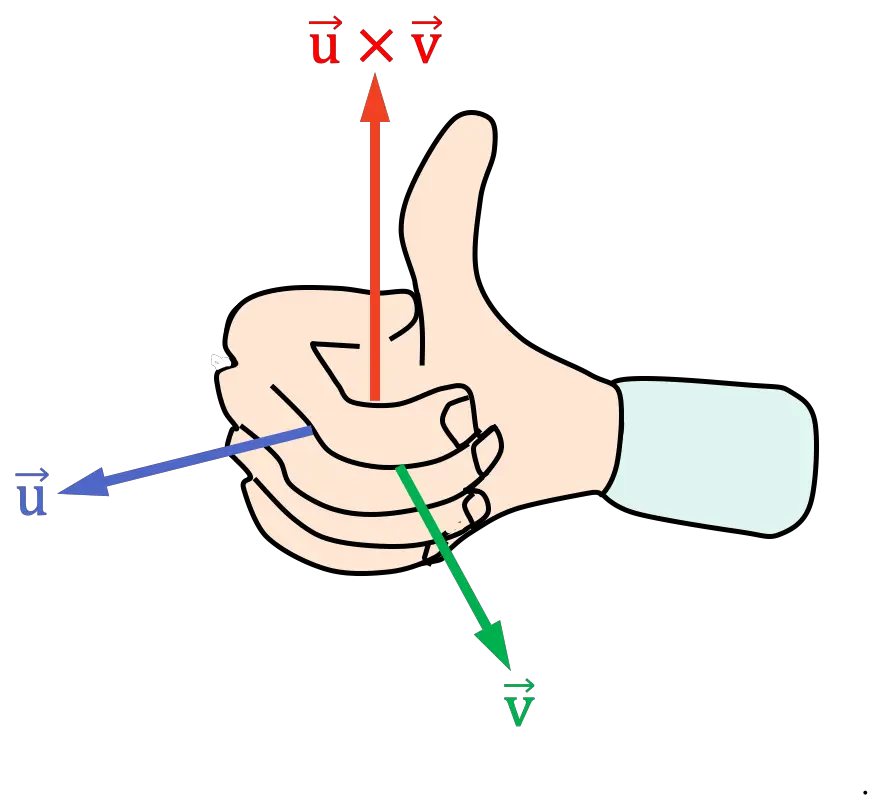
Korkenzieherregel

Die Korkenzieher- oder Schraubenregel ähnelt der Regel für die rechte Hand und verwendet die gesamte Handfläche. Das Verfahren ist wie folgt:

Platzieren Sie mit Ihrer Fantasie einen Korkenzieher (oder eine Schraube), wobei der Griff in die gleiche Richtung zeigt wie der erste Vektor des Kreuzprodukts.
$(\vv{\text{u}}).$
Drehen Sie dann den Korkenzieher in Richtung des zweiten Vektors des Kreuzprodukts
$(\vv{\text{v}})$

als würde man es in einen Korken stecken. Sie müssen den Korkenzieher auf die Seite drehen, auf der der Abstand zwischen den Vektoren am kürzesten ist.
Die Richtung, in die die Korkenzieherspirale zeigt, ist die Richtung und Richtung des Vektorprodukts
$(\vv{\text{u}}\times\vv{\text{v}}).$

Eigenschaften des Kreuzprodukts zweier Vektoren

Das Kreuzprodukt zweier Vektoren weist folgende Eigenschaften auf:

Antikommutative Eigenschaft: Die Reihenfolge der am Vektorprodukt beteiligten Vektoren ist nicht gleichgültig, da das Vorzeichen entsprechend variiert.

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

Verteilungseigenschaft bezüglich der Addition und Subtraktion von Vektoren:

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

Homogene Eigenschaft : Die Multiplikation eines Vektors des Kreuzprodukts mit einem Skalar (einer reellen Zahl) ist äquivalent zur Multiplikation des Ergebnisses des Kreuzprodukts mit diesem Skalar.

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

Der aus dem Vektorprodukt resultierende Vektor steht senkrecht auf den beiden an der Operation beteiligten Vektoren.

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

Wenn die beiden Vektoren außerdem orthogonal sind, sind die folgenden Gleichungen erfüllt:

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

Das Kreuzprodukt zweier paralleler Vektoren ist gleich dem Nullvektor (oder Null).

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

Wenn wir den von zwei Vektoren gebildeten Winkel nicht kennen, kann der Modul ihres Vektorprodukts auch mit dem folgenden Ausdruck berechnet werden:

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

Berechnen Sie die Fläche eines Parallelogramms oder Dreiecks mithilfe des Kreuzprodukts

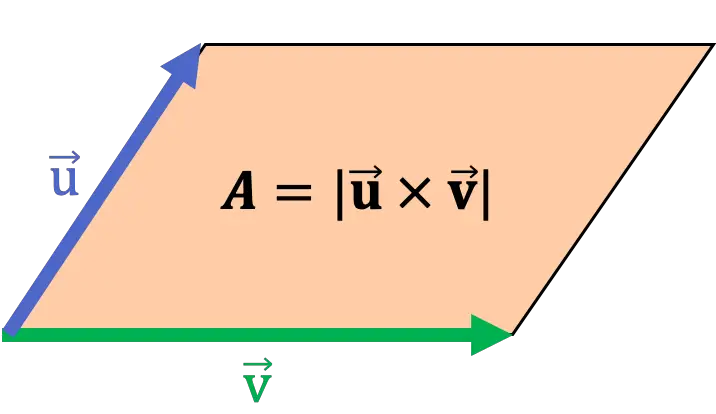
Geometrisch gesehen stimmt der Modul des Kreuzprodukts zweier Vektoren mit der Fläche des Parallelogramms überein, dessen Seiten diese beiden Vektoren sind. Daher kann das Kreuzprodukt zur Berechnung der Fläche eines Parallelogramms verwendet werden.

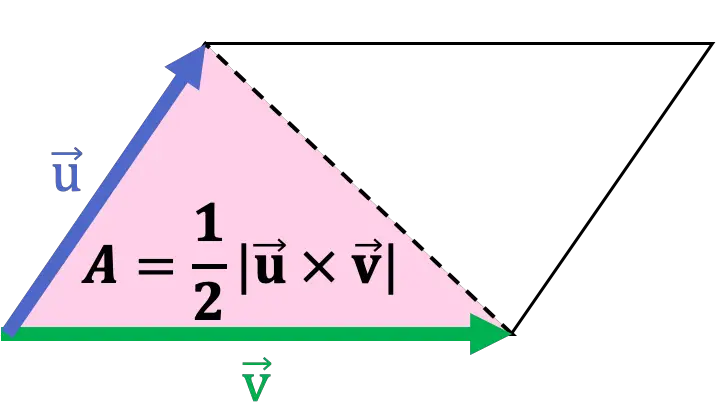
Darüber hinaus teilt die Diagonale ein Parallelogramm in zwei Dreiecke, oder anders ausgedrückt: Ein Dreieck ist die Hälfte eines Parallelogramms. Somit ist die Fläche eines Dreiecks die Hälfte des Moduls des Kreuzprodukts, das zwei seiner Seiten als Vektoren nimmt.

Denken Sie daran, dass der Modul eines Vektors in einem dreidimensionalen Raum die Wurzel der Summe der Quadrate seiner Koordinaten ist:

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Dies sind zwei der Anwendungen des Kreuzprodukts zweier Vektoren im Bereich der Mathematik. Es gibt jedoch noch andere Verwendungszwecke, beispielsweise wird es in der Physik zur Berechnung des Magnetfelds verwendet.

Gelöste Übungen zu Vektorprodukten von Vektoren

Übung 1

Berechnen Sie das Kreuzprodukt zwischen den folgenden beiden Vektoren:

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

Sehen Sie sich die Lösung an

Um das Vektorprodukt zwischen den Vektoren zu bestimmen, müssen wir die folgende Determinante der Dimension 3×3 lösen:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

In diesem Fall lösen wir die Determinante durch Adjuvanzien oder Cofaktoren (es könnte aber auch die Sarrus-Regel verwendet werden):

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

Das Ergebnis des Vektorprodukts der beiden Vektoren ist daher:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

Übung 2

Finden Sie das Kreuzprodukt zwischen den folgenden beiden Vektoren:

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

Sehen Sie sich die Lösung an

Um das Vektorprodukt zwischen den beiden Vektoren zu finden, müssen wir die folgende 3×3-Determinante lösen:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

In diesem Fall werden wir die Determinante mithilfe von Adjunkten oder Cofaktoren auflösen (obwohl die Regel von Sarrus austauschbar verwendet werden kann):

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

Das Ergebnis des Vektorprodukts zwischen den beiden Vektoren ist daher:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

Übung 3

Kenntnis der Module zweier Vektoren und des Winkels, den sie bilden:

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

Bestimmen Sie den Betrag des Kreuzprodukts der beiden Vektoren.

Sehen Sie sich die Lösung an

Wir können den Modul des Vektorprodukts zwischen den beiden Vektoren leicht berechnen, indem wir die Formel anwenden:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

Übung 4

Aus den folgenden in der Bildschirmebene enthaltenen Vektoren:

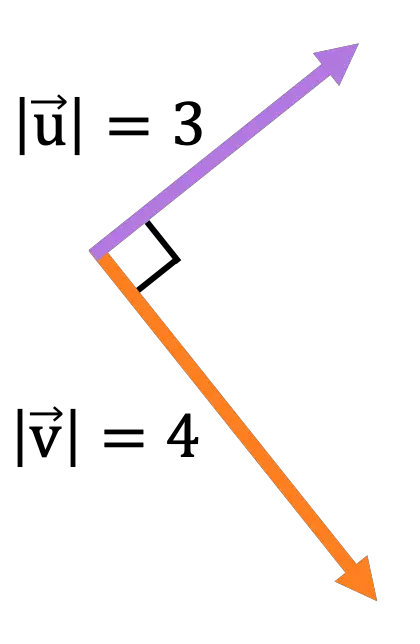
Kreuzprodukt zweier Vektoren in einer Linie

Berechnen Sie Betrag, Richtung und Sinn des Vektors, der sich aus der folgenden Vektoroperation ergibt:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

Sehen Sie sich die Lösung an

Da die beiden Vektoren senkrecht zueinander stehen, lautet die Norm des Vektorprodukts:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

Andererseits ist der aus dem Vektorprodukt resultierende Vektor senkrecht zu den beiden an der Operation beteiligten Vektoren, seine Richtung ist daher senkrecht zum Bildschirm.

Und schließlich können wir mithilfe der Geraden- (oder Korkenzieher-)Regel ableiten, dass die Richtung des resultierenden Vektors zur Innenseite des Bildschirms zeigt.

Übung 5

Berechnen Sie die Fläche des Parallelogramms, dessen zwei Seiten die folgenden Vektoren sind:

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

Sehen Sie sich die Lösung an

Die Fläche eines Parallelogramms stimmt mit dem Modul des Kreuzprodukts der Vektoren überein, die es bilden. Wir berechnen daher das Vektorprodukt der Vektoren:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

Und dann Ihr Modul:

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

Übung 6

Finden Sie die Fläche des Dreiecks, dessen Eckpunkte die folgenden Punkte sind:

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

Sehen Sie sich die Lösung an

Zunächst müssen wir die Vektoren berechnen, die die Seiten des Dreiecks bilden:

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

Die Fläche eines Dreiecks ist halb so groß wie das Vektorprodukt der Vektoren, aus denen es besteht. Wir berechnen daher das Vektorprodukt der Vektoren:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

Nach Ihrem Modul:

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

Und schließlich beträgt die Fläche des Dreiecks die Hälfte des Moduls:

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

Kreuzprodukt zweier vektoren (oder kreuzprodukt)

Was ist das Kreuzprodukt zweier Vektoren?

Formel zur Berechnung des Kreuzprodukts zweier Vektoren

Bestimmt die Richtung und Richtung des Kreuzprodukts

Regel der rechten Hand (3 Finger)

Regel der rechten Hand (Handfläche)

Korkenzieherregel

Eigenschaften des Kreuzprodukts zweier Vektoren

Berechnen Sie die Fläche eines Parallelogramms oder Dreiecks mithilfe des Kreuzprodukts

Gelöste Übungen zu Vektorprodukten von Vektoren

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Übung 6

Kommentar verfassen Kommentieren abbrechen