Koplanare (oder koplanare) Vektoren

Auf dieser Seite erfahren Sie, was koplanare Vektoren sind und wie Sie feststellen können, ob 2, 3, 4 oder mehr Vektoren koplanar sind. Darüber hinaus können Sie Beispiele und Übungen sehen, die Schritt für Schritt zu koplanaren Vektoren gelöst werden.

Was sind koplanare Vektoren?

In der analytischen Geometrie haben koplanare (oder koplanare) Vektoren folgende Bedeutung:

Koplanare Vektoren sind Vektoren, die zur gleichen Ebene gehören.

Daher sind zwei Vektoren immer koplanar, da eine Ebene mit nur zwei Vektoren gebildet werden kann. Wenn andererseits 3, 4 oder mehr Vektoren vorhanden sind, ist es möglich, dass einer der Vektoren nicht in derselben Ebene liegt und sie daher nicht koplanar sind.

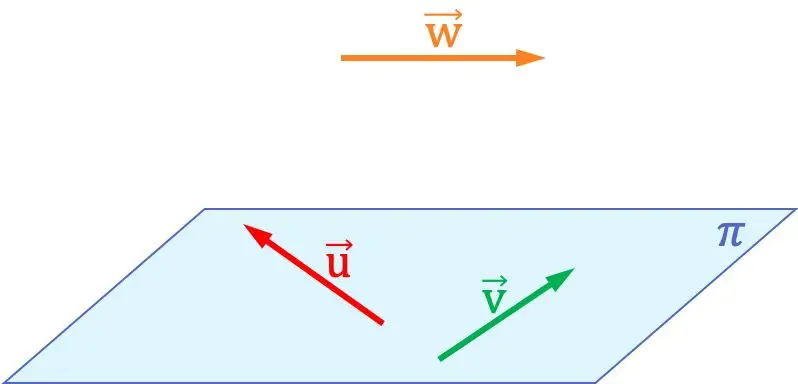
Beispiele für koplanare oder koplanare Vektoren

In der Grafik oben können Sie beispielsweise sehen, dass die Vektoren

$\vv{\text{u}}$

Und

$\vv{\text{v}}$

sie sind koplanar zueinander, da sie in derselben Ebene liegen. Andererseits sind diese beiden Vektoren nicht koplanar mit dem Vektor

$\vv{\text{w}}$

, weil in dem Raum, der die drei Vektoren enthält, keine Ebene gebildet werden kann.

Aus dieser Eigenschaft können wir ableiten, dass, wenn drei oder mehr Vektoren koplanar sind, die Punkte, die diese Vektoren definieren (Anfang und Ende des Vektors), ebenfalls koplanare Punkte sind.

Wann sind Vektoren koplanar?

Wie wir bei der Definition koplanarer (oder koplanarer) Vektoren gesehen haben, sind zwei Vektoren immer koplanar, aber mehr als zwei Vektoren müssen die Koplanaritätsbeziehung nicht respektieren.

Daher gibt es mehrere Methoden, um zu bestimmen, ob drei oder mehr Vektoren koplanar sind:

Wenn das gemischte Produkt dreier Vektoren (oder das Dreifachskalarprodukt) gleich Null ist, bedeutet dies, dass die drei Vektoren koplanar sind. Wenn Sie nicht genau wissen, wie diese Operation berechnet wird, empfehle ich Ihnen, einen Blick auf das gemischte Produkt dreier Vektoren zu werfen. Hier finden Sie die Erklärung sowie Beispiele und gelöste Übungen.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] =0$

Wenn eine Menge von Vektoren als lineare Kombination zweier Vektoren ausgedrückt werden kann, impliziert dies, dass sie koplanar sind, was bedeutet, dass 3 oder mehr Vektoren genau dann koplanar sind, wenn sie linear abhängig sind. Um zu zeigen, dass drei oder mehr Vektoren eine Linearkombination zweier Vektoren sind, reicht es aus, wenn der Rang der aus allen Vektoren gebildeten Matrix gleich 2 ist.

$rg(A) = 2$

Es ist wichtig, dass Sie das Konzept der linearen Abhängigkeit und Unabhängigkeit gut verstehen, das heißt, wann zwei Vektoren linear abhängig oder linear unabhängig sind und was das bedeutet. Wenn Sie nicht ganz klar sind, finden Sie im Link eine sehr ausführliche Erklärung, in der Sie außerdem Beispiele und Schritt für Schritt gelöste Übungen sehen können.

Wenn es sich bei den betreffenden Vektoren um Parallelvektoren handelt, bedeutet dies, dass sie auch koplanar sind, das heißt, alle Parallelvektoren liegen in derselben Ebene.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Probleme koplanarer Vektoren gelöst

Übung 1

Bestimmen Sie, ob die folgenden drei Vektoren koplanar sind:

$\vv{\text{u}} = (3,1,2)$

$\vv{\text{v}} = (2,3,-1)$

$\vv{\text{w}} = (-1,-5,4)$

siehe Lösung

Um zu überprüfen, ob es sich um drei koplanare Vektoren handelt, müssen wir das gemischte Produkt zwischen den drei Vektoren berechnen:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}$

Das gemischte Produkt der drei Vektoren ist Null, die drei Vektoren sind also koplanar .

Übung 2

Bestimmen Sie, ob die folgenden drei Vektoren koplanar sind:

$\vv{\text{u}} = (4,-2,6)$

$\vv{\text{v}} = (-2,1,-3)$

$\vv{\text{w}} = (6,-3,9)$

siehe Lösung

Eine Möglichkeit zu überprüfen, ob es sich um drei koplanare Vektoren handelt, wäre die Lösung nach dem gemischten Produkt zwischen den drei Vektoren. Wenn wir uns jedoch die Komponenten der Vektoren genau ansehen, können wir erkennen, dass sie proportional sind. Daher sind die drei Vektoren parallel zueinander.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Und da alle Vektoren parallel sind, handelt es sich effektiv um drei koplanare Vektoren .

Übung 3

Bestimmen Sie, ob die folgenden vier Vektoren koplanar sind:

$\vv{\text{a}} = (2,1,1)$

$\vv{\text{b}} = (1,-1,2)$

$\vv{\text{c}} = (-1,0,-1)$

$\vv{\text{d}} = (3,1,2)$

siehe Lösung

Um zu wissen, ob die vier Vektoren koplanar sind, müssen wir den Rang der Matrix berechnen, die aus allen Vektoren besteht:

$\displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}$

In diesem Fall berechnen wir den Umfang dieser Matrix anhand von Determinanten:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0$