Konstante Funktion

In diesem Artikel erklären wir, was eine konstante Funktion ist und wie sie grafisch dargestellt wird. Darüber hinaus können Sie mehrere Beispiele für konstante Funktionen und alle Merkmale dieses Funktionstyps sehen. Und schließlich können Sie mit gelösten Übungen konstanter Funktionen trainieren.

Was ist eine konstante Funktion?

Eine konstante Funktion ist die Funktion, die für jeden Wert der unabhängigen Variablen (x) immer das gleiche Bild annimmt , dh eine konstante Funktion hat die Form f(x)=k , wobei k eine beliebige reelle Zahl ist.

$f(x)=k$

Die grafische Darstellung einer konstanten Funktion ist eine horizontale Linie.

Alle folgenden Funktionen sind beispielsweise Konstanten:

$f(x)=1 \qquad f(x)=7 \qquad f(x)=5$

Grafische Darstellung einer konstanten Funktion

Sobald wir das Konzept einer konstanten Funktion kennengelernt haben, werden wir sehen, wie man eine konstante Funktion in einem Diagramm darstellt.

Die grafische Darstellung einer konstanten Funktion ist recht einfach. Zeichnen Sie einfach eine horizontale Linie im Wert der Funktion (k).

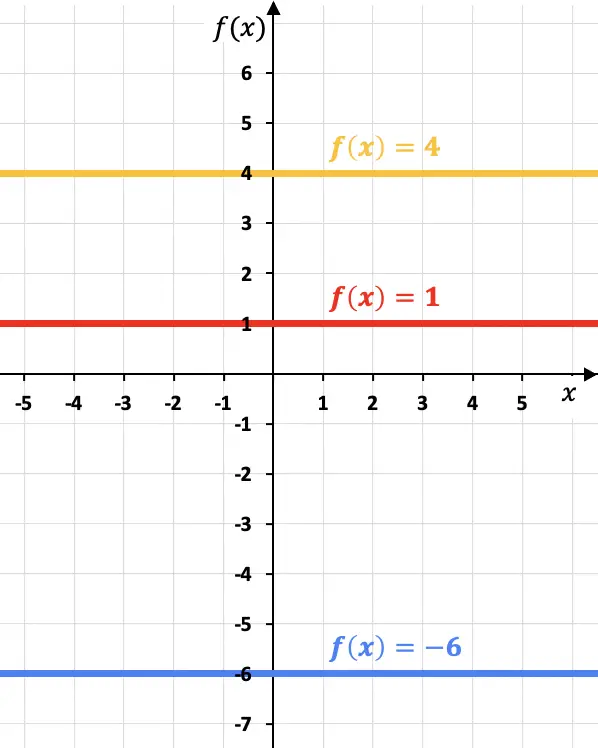
Schauen Sie sich die folgenden Beispiele an, in denen wir drei verschiedene konstante Funktionen in einem Diagramm dargestellt haben:

Beachten Sie, dass jede konstante Funktion parallel zur x-Achse verläuft.

Andererseits muss man bedenken, dass eine vertikale Linie keine konstante Funktion ist. Tatsächlich ist eine vertikale Linie nicht einmal eine Funktion, da eine Funktion per Definition nur ein Bild für jeden Wert von x haben kann.

Eigenschaften der konstanten Funktion

Als nächstes analysieren wir die Eigenschaften der konstanten Funktion. Betrachten Sie eine konstante Funktion mit beliebigem Wert:

$f(x)=k$

Der Definitionsbereich der konstanten Funktion sind alle reellen Zahlen:

$\text{Dom } f = \mathbb{R}$

Der Pfad oder Bereich der konstanten Funktion ist nur der Wert der Konstante:

$\text{Im } f= k$

Es handelt sich um eine stetige und gerade Funktion, da die Funktion immer den gleichen Wert annimmt:

$\displaystyle f(x)=f(-x)$

Die konstante Funktion ist weder steigend noch fallend, es handelt sich um einen Funktionstyp, der immer eine Steigung von Null hat:

$m=0$

Es schneidet die OY-Achse immer im Punkt (0,k).

$(0,k)$

Jede konstante Funktion ist ein Polynom vom Grad Null.

Ja
$k\neq 0$

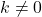
Die konstante Funktion hat keine Wurzel, sondern if

$k=0$

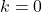
Alle reellen Zahlen sind die Wurzeln der konstanten Funktion.

Der Grenzwert der konstanten Funktion, wenn x sich Plus-Unendlich oder Minus-Unendlich nähert, ist gleich dem Wert der Konstante:

$\displaystyle\lim_{x\to +\infty} f(x)=k$

$\displaystyle\lim_{x\to -\infty} f(x)=k$

Die Ableitung der konstanten Funktion ist immer Null:

$f(x)=k \ \longrightarrow \ f'(x)=0$

Tatsächlich kann die Definition der konstanten Funktion auch anhand des Begriffs der Ableitung erfolgen: Eine Funktion ist konstant, wenn ihre Ableitung über ihren gesamten Bereich verschwindet.

Das Integral der konstanten Funktion ist die lineare (oder affine) Funktion:

$\displaystyle \int k \ dx= x + C$

➤ Siehe: Was ist eine lineare Funktion?

Konstante Funktion in einem Intervall

Wir haben gesehen, dass eine Funktion konstant ist. Allerdings kann eine Funktion nur in einem Intervall ihres Definitionsbereichs konstant sein.

Um dieses Konzept zu verstehen, müssen Sie wissen, welche Funktionen in Blöcken definiert sind. Bevor Sie fortfahren, empfehlen wir Ihnen daher, einen Blick auf die folgende Erklärung zu werfen:

➤ Siehe: Was ist eine stückweise Funktion?

Wenn Sie wissen, um welche Art von Funktionen es sich handelt, sehen Sie sich die in den folgenden Teilen definierte Funktion an:

Wie Sie der Grafik entnehmen können, ist die Funktion nicht über alle Zahlen in ihrem Definitionsbereich hinweg konstant. Sie ist aber im Intervall [-2,4) konstant, also nur in einem Intervall eine konstante Funktion.