Auf dieser Seite finden Sie die Definition von Kegelschnitten, warum sie so wichtig sind und welche verschiedenen Arten von Kegelschnitten es gibt (Kreis, Ellipse, Hyperbel und Parabel). Darüber hinaus können Sie die Unterschiede zwischen ihren Gleichungen erkennen.
Was sind Kegelschnitte?
In der analytischen Geometrie sind Kegelschnitte (oder einfach Kegelschnitte) alle Kurven, die sich aus den verschiedenen Schnittpunkten zwischen einem Kegel und einer Ebene ergeben, wenn diese Ebene nicht durch die Spitze des Kegels verläuft. Es gibt vier Arten von Kegelschnitten: den Kreis, die Ellipse, die Parabel und die Hyperbel.
Nachfolgend sind die 4 möglichen Abschnitte aufgeführt, die aus jedem Kegel erhalten werden können:
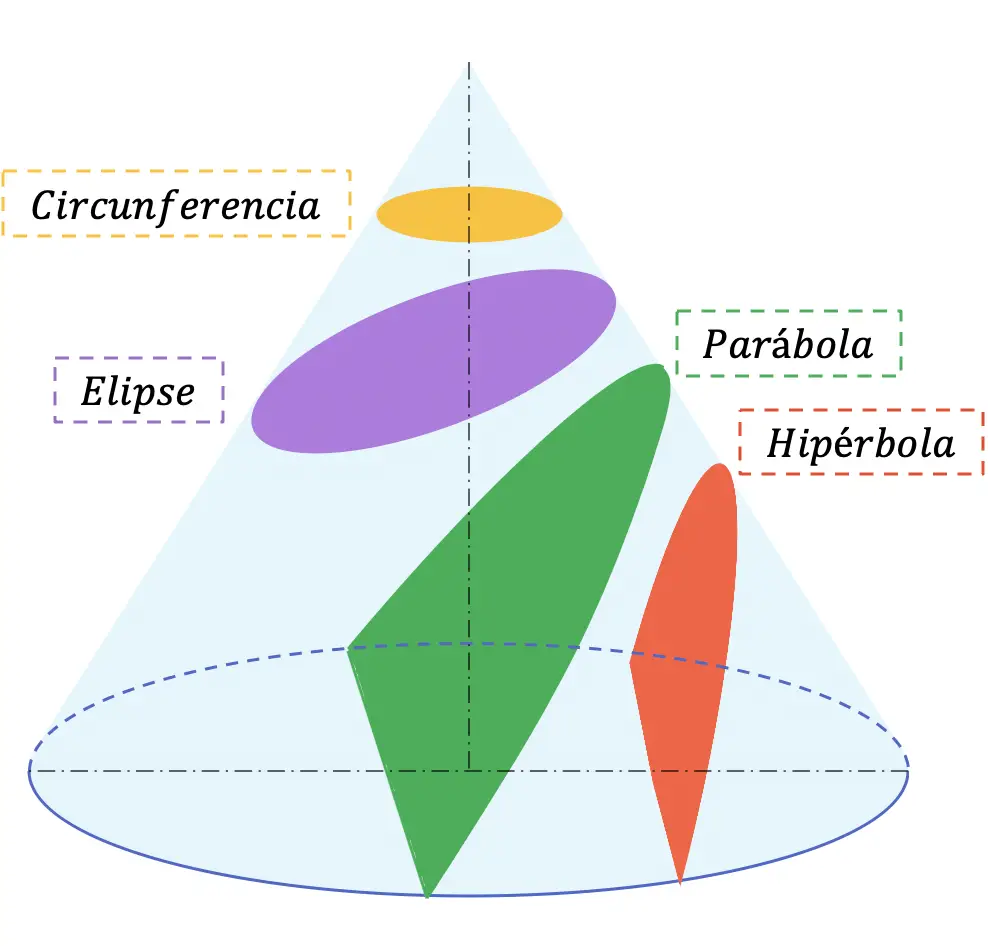
Kegelschnitte werden in der Regel in der weiterführenden Schule (Bachillerato) in den Fächern Mathematik und technisches Zeichnen studiert.
Arten von Kegelschnitten
Nachdem wir das Konzept des Kegelschnitts kennengelernt haben, wollen wir uns die vier Arten von Kegelschnitten ansehen, die es gibt: den Kreis, die Ellipse, die Parabel und die Hyperbel.
Umfang
Der Umfang ist ein konischer Abschnitt, den man erhält, indem man einen Kegel mit einer Ebene senkrecht zu seiner Rotationsachse (parallel zur Basis) schneidet.
Darüber hinaus ist der Umfang der Ort der Punkte auf der Ebene, die von einem festen Punkt, dem Mittelpunkt, gleich weit entfernt sind.
Ellipse
Die Ellipse ist eine flache, geschlossene, gekrümmte Linie, die dem Umfang sehr ähnlich ist, ihre Form jedoch eher oval ist. Sie entsteht insbesondere dadurch, dass die Oberfläche eines Kegels durch eine schiefe Ebene geschnitten wird, deren Winkel relativ zur Rotationsachse größer ist als der des Generators.
Darüber hinaus erfüllen alle Punkte einer Ellipse eine Bedingung: Die Ellipse ist der Ort aller Punkte einer Ebene, deren Summe der Abstände zu zwei anderen festen Punkten (genannt Brennpunkte F und F‘) konstant ist.
Gleichnis
In der Mathematik ist eine Parabel der Ort von Punkten auf der Ebene, die den gleichen Abstand von einem festen Punkt (genannt Fokus) und einer festen Linie (genannt Leitlinie) haben.
Geometrisch gesehen ist die Parabel das Ergebnis des Schnitts eines Kegels durch eine Ebene mit einem Neigungswinkel relativ zur Rotationsachse, der dem Winkel der Erzeugenden des Kegels entspricht. Daher ist die Ebene, die die Parabel enthält, parallel zum Generator des Kegels.
Ein sehr wichtiges Merkmal dieses Kegelschnitts ist die Parabelgleichung , denn anhand ihres Zustands können wir erkennen, um welche Art von Parabel es sich handelt. In diesem Link finden Sie alle Gleichungen der Parabel, was sind die Elemente der Parabel, ihre Eigenschaften, Beispiele, gelöste Übungen usw. und andere Eigenschaften von Parabeln.
Hyperbel
Als Kegelschnitt entsteht eine Hyperbel, wenn ein Kegel von einer Ebene mit einem Winkel geschnitten wird, der kleiner ist als der Winkel, den der Generator des Kegels mit seiner Rotationsachse bildet.
Mathematisch kann eine Hyperbel als Ort von Punkten auf der Ebene definiert werden, die die folgende Eigenschaft erfüllen: Der Absolutwert der Abstandsdifferenz zwischen einem beliebigen Punkt auf der Hyperbel und zwei festen Punkten (Brennpunkten genannt) muss konstant sein.
Darüber hinaus entspricht der Wert der Subtraktion dieser beiden Abstände immer dem Abstand zwischen den beiden Eckpunkten der Hyperbel.
Wie Sie sicher schon herausgefunden haben, der Parameterwert
einer Hyperbel ist grundlegend für Hyperbeln. Unter dem folgenden Link können Sie unsere Erklärung der Hyperbel sehen. Dort erfahren Sie, warum sie ein so wichtiger Koeffizient ist und welche Elemente eine Hyperbel charakterisieren. Außerdem erfahren Sie, wie die Gleichung einer Hyperbel aussieht, welche verschiedenen Arten von Hyperbeln es gibt und sogar Schritt-für-Schritt-Aufgaben und Übungen zu Hyperbeln.
Allgemeine Kegelschnittgleichung
Jeder Kegelschnitt kann analytisch als Gleichung ausgedrückt werden. Tatsächlich müssen alle Kegelgleichungen zweiten Grades sein:
Folglich mindestens einer der Koeffizienten
entweder
der Formel muss ungleich Null sein.
Abhängig von den Parameterwerten entspricht die Gleichung also dem einen oder anderen Kegeltyp:
- Umfang : für die allgemeine Gleichung, die einen Umfang beschreibt, die Terme
Und
muss übereinstimmen und
muss Null sein.
- Ellipse : Die Gleichung entspricht dem mathematischen Ausdruck einer Ellipse, wenn die folgende Bedingung erfüllt ist:
- Parabel : Damit die Gleichung eine Parabel ist, muss die folgende Gleichung erfüllt sein:
- Hyperbel : Schließlich muss die allgemeine Gleichung einer Hyperbel die folgende Ungleichung erfüllen:
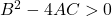Beitrags-Navigation