Komplexe Zahlen

Sie haben wahrscheinlich schon von komplexen Zahlen gehört. Sie sind möglicherweise die am schwierigsten zu handhabende Zahlenmenge, da sie reale und imaginäre Zahlen kombinieren. Seine Vereinheitlichung ermöglicht die Untersuchung numerischer Verhaltensweisen, die nicht mit allen reellen Zahlen behandelt werden können.

Was sind komplexe Zahlen?

Komplexe Zahlen sind die Kombination einer reellen Zahl und einer imaginären Zahl . Beispielsweise ist 4 + 5i eine komplexe Zahl, deren Realteil gleich 4 und deren Imaginärteil gleich 5i ist. Im Allgemeinen können wir sie durch die folgende Formel ausdrücken:

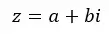
Wobei Re(z) = a und Im(z) = b

Wie wir schon sagten, sind Komplexe die größte Menge oder globale Menge , die sowohl reelle als auch imaginäre Zahlen umfasst. Als nächstes zeigen wir Ihnen ein kleines Diagramm der hierarchischen Struktur aller Mengen:

Wenn wir also eine Kombination aus einer reellen Zahl und einer imaginären Zahl haben, haben wir eine komplexe Zahl. Es gibt jedoch Zeiten, in denen einer der beiden Teile gleich Null ist. Was passiert in diesen Fällen? Nun, wir haben es immer noch mit Komplexen zu tun, denn die komplexe Menge umfasst alle anderen numerischen Mengen. Aber wir geben eine andere Unterkategorie ein:

komplexe Zahl	königliche Partei	Fantasieteil	Unterkategorie
2+5i	2	5i	Komplex
4	4	0	rein königlich
3i	0	3i	Pure Fantasie

Wenn wir eine reine reelle Zahl haben, da der imaginäre Wert b gleich Null ist, ist die verbleibende komplexe Zahl äquivalent zu:

z = a + 0i = a

Wenn wir hingegen eine reine Vorstellungskraft haben, ist a gleich Null und folglich bleibt die komplexe Zahl die folgende:

z = 0 + bi = bi

Grafische Darstellung komplexer Zahlen

Um komplexe Zahlen darzustellen, verwenden wir die komplexe Ebene . Die aus zwei Linien besteht: der realen Linie und der imaginären Linie. Diese beiden Zahlenlinien werden verwendet, um die Zahlen in jedem Satz grafisch zu lokalisieren, und wenn wir sie zusammenfügen, erhalten wir einen Plan, wie zum Beispiel:

Die X-Achse wird Realachse genannt, da sich dort die Realteilwerte befinden. Während die Y-Achse als imaginäre Achse bezeichnet wird, werden hier die imaginären Werte geschrieben. Sehen wir uns ein Beispiel an: Wir werden die Zahl 3 + 2i in der komplexen Ebene platzieren.

Wie Sie im Bild gesehen haben, haben wir die Zahl anhand der Zahlen 3 und 2 als Koordinaten ermittelt, jeweils für eine Achse. Wenn Sie mehr über die Darstellung komplexer Zahlen erfahren möchten, empfehlen wir Ihnen die Lektüre dieses Artikels.

Welche Arten komplexer Zahlen gibt es?

Jetzt werden wir sehen, wie wir eine komplexe Zahl ausdrücken können. Bisher haben wir nur die Grundform (die sogenannte Binomialform) gesehen, die als Summe geschrieben wird: Realteil plus Imaginärteil.

Aber in Wirklichkeit haben wir drei Formen: die binomiale, die polare und die trigonometrische . Jeder Ausdruckstyp hat seine Eigenschaften und wird in der einen oder anderen Situation verwendet. Deshalb werden wir sie alle erklären und zeigen, wie man von einem zum anderen wechselt.

1. Binomialform

Komplexe Zahlen in Binomialform werden als Summe des Realteils und des Imaginärteils geschrieben: a + bi. Beispielsweise ist die Zahl 6 + i ein Komplex, der in Binomialschreibweise ausgedrückt wird. In diesem Fall ist die Formel immer dieselbe:

Um eine komplexe Zahl in Binomialform auszudrücken, müssen Sie daher nur ihren realen Wert und ihren imaginären Wert kennen.

Beispielsweise liegt der Wert 3 + 2i in Binomialform vor und wird, wie wir zuvor gesehen haben, wie folgt dargestellt:

Die Binomialform wird hauptsächlich zur Lösung der Addition und Subtraktion komplexer Zahlen verwendet.

2. Polarform

Um komplexe Zahlen in Polarform auszudrücken, müssen wir ihren Modul |z| berechnen und seine Argumentation. Die Polarform wird hauptsächlich verwendet, wenn wir Multiplikationen und Divisionen komplexer Zahlen lösen müssen.

Um den Modul der komplexen Zahl zu berechnen , berechnen Sie einfach den Modul von a und b, wie in der folgenden Formel erläutert:

Und um das Argument oder den Winkel von z zu berechnen , müssen wir den Arkustangens von b zwischen a berechnen:

Es ist wichtig zu beachten, dass zur genauen Bestimmung des Winkels α zunächst ermittelt werden muss, in welchem Quadranten er sich befindet. Tatsächlich berechnet die Arkustangensfunktion nur Winkel zwischen π/2 und -π/2. Um anzugeben, in welchem Quadranten sich die komplexe Zahl befindet, müssen wir uns die Werte a und b ansehen (ob sie positiv oder negativ sind):

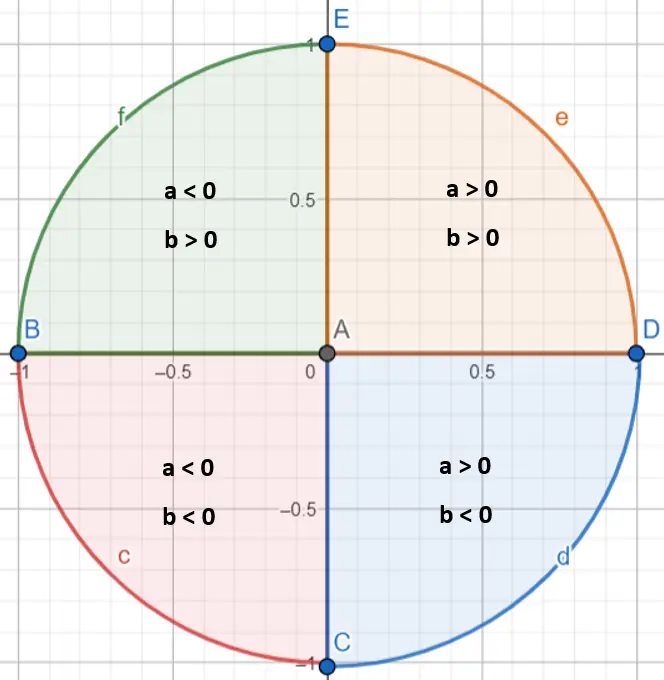
Sobald wir wissen, in welchen Quadranten unsere Zahl fällt, müssen wir einige Regeln befolgen:

Wenn die komplexe Zahl im ersten Quadranten liegt (a > 0 und b > 0), lassen wir das Argument unverändert.
Wenn die komplexe Zahl im zweiten Quadranten liegt (a < 0 und b > 0), addieren wir π zum Argument.
Liegt die komplexe Zahl im dritten Quadranten (a < 0 und b < 0), subtrahieren wir π vom Argument.
Wenn die komplexe Zahl im vierten Quadranten liegt (a > 0 und b < 0), addieren wir 2π zum Argument.

Falls Sie nicht wissen, wovon wir sprechen, wenn wir Quadranten sagen, empfehlen wir Ihnen, unseren Artikel über trigonometrische Verhältnisse zu lesen.

Sobald wir den Betrag und das Argument von z kennen, können wir die komplexe Zahl in Polarform ausdrücken. Obwohl dieses Formular mehrere Nomenklaturen akzeptiert, sind die beiden wichtigsten:

Wenn wir beispielsweise die Zahl 3 + 5i in polar ändern möchten, müssen wir lediglich das folgende Verfahren befolgen.

Wir berechnen zunächst das Modul:

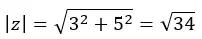
Dann berechnen wir das Argument, das im ersten Quadranten liegt, sodass es so bleibt, wie wir es berechnet haben.

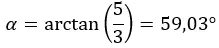
Und wir drücken die Zahl in Polarform aus:

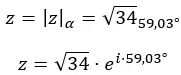
Die grafische Darstellung sieht wie folgt aus:

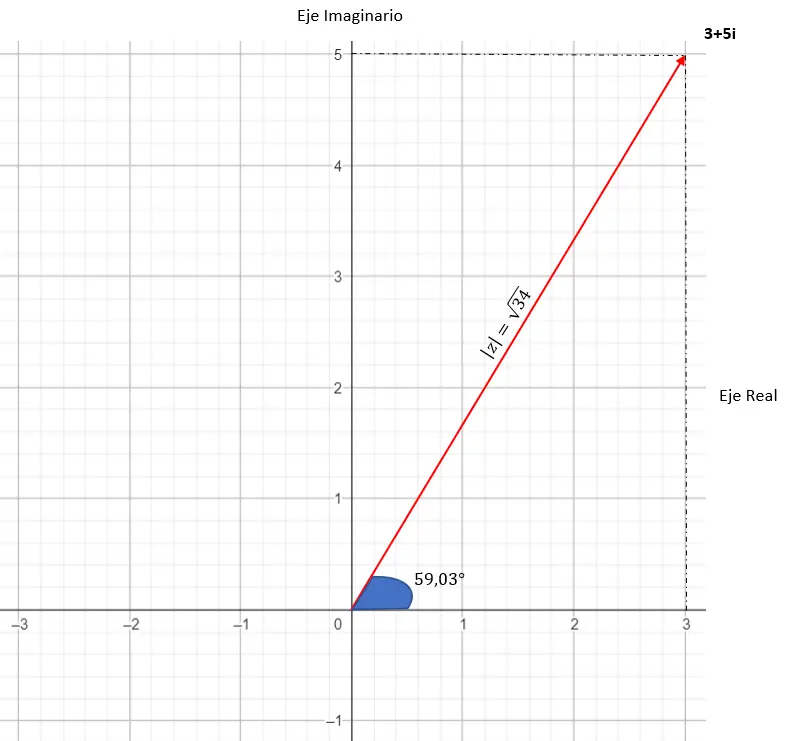
Grafische Darstellung einer komplexen Zahl in Polarform

3. Trigonometrische Form

Schließlich haben wir die trigonometrische Notation , die aus der Euler-Formel berechnet wird:

Um beispielsweise die Zahl 4 – 3i in trigonometrischer Form auszudrücken, gehen wir wie folgt vor:

Wir beginnen mit der Berechnung des Moduls und des Arguments mit den Formeln, die wir im Abschnitt zur Polarform verwendet haben.

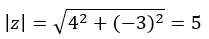
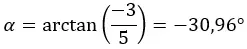
ACHTUNG: Das Argument liegt im vierten Quadranten, weil (a > 0 und b < 0).

Wir fügen die Daten in trigonometrischer Form in die Gleichung ein.

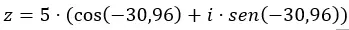
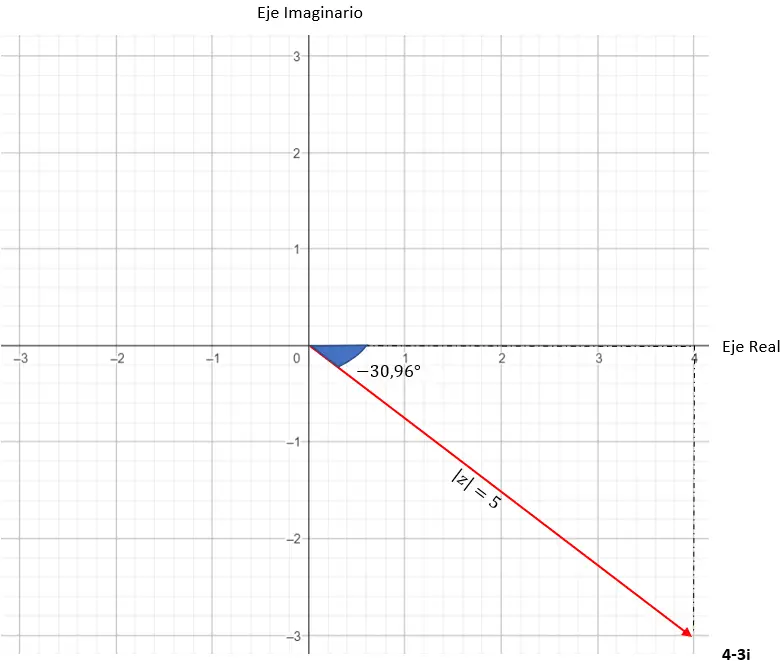
Und wir haben bereits die Zahl in trigonometrischer Form ausgedrückt. Seine grafische Darstellung ist wie folgt.

Grafische Darstellung einer komplexen Zahl in trigonometrischer Form

Wie wechselt man von einem Typ zum anderen?

Sie kennen jetzt alle Möglichkeiten, eine komplexe Zahl auszudrücken. Im letzten Abschnitt konnten Sie sehen, wie Sie auf die einzelnen Formulare zugreifen können. Bevor wir jedoch fertig sind, möchten wir noch kurz zusammenfassen, wie Sie von einem Formular zum anderen wechseln. Sie müssen lediglich die Formeln verwenden, die wir im vorherigen Abschnitt gesehen haben.

Von der binomischen zur polaren Form und umgekehrt

Um von binomial zu polar zu gelangen, schlagen wir das folgende Diagramm vor:

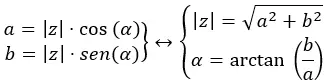
Wir haben vorhin ein Beispiel gesehen, bei dem wir vom Binomialwert zum Polarwert übergegangen sind. Jetzt gehen wir mithilfe des Diagramms oben vom Polarwert zum Binomialwert über. Wir müssen √41 _38,66 in ein Binomial umwandeln.

Wir berechnen zunächst das a.

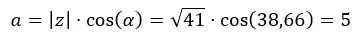
Dann berechnen wir b.

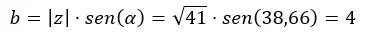
Und wir drücken es in Binomialform aus.

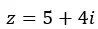
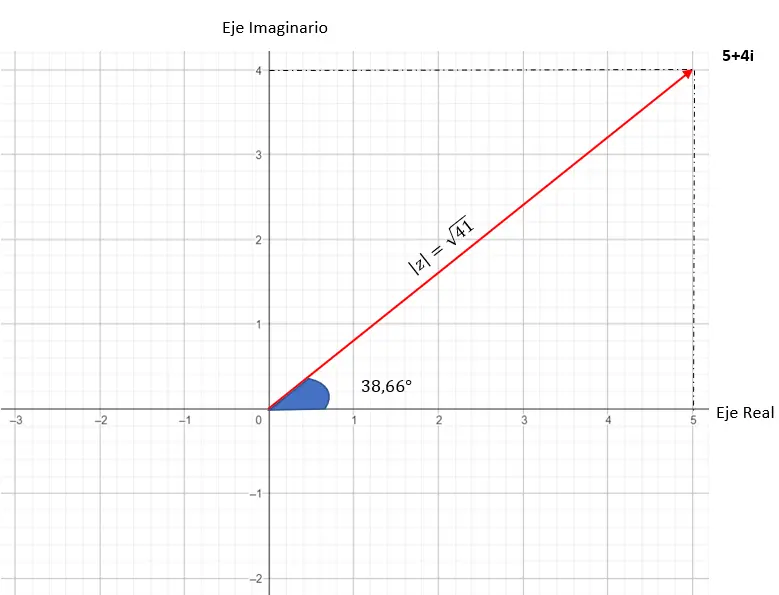
Die grafische Darstellung dieser Zahl sieht folgendermaßen aus:

Von der Binomialform zur trigonometrischen Form und umgekehrt

Um von binomial zu trigonometrisch zu gelangen, müssen Sie auch die Formeln anwenden, über die wir im vorherigen Abschnitt gesprochen haben. Auf diese Weise berechnen wir zunächst den Modul und das Argument und setzen diese Daten dann in die Gleichung der trigonometrischen Form ein. Um ein Beispiel zu geben, übergeben wir die Zahl z = 3 + 2i trigonometrisch.

Wir berechnen zunächst den Modul und das Argument.

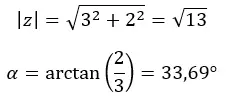
ACHTUNG: Das Argument liegt im ersten Quadranten, weil (a > 0 und b > 0).

Anschließend vervollständigen wir die trigonometrische Formgleichung mit diesen Daten.

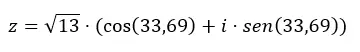
Und wenn wir von trigonometrisch zu binomial wechseln wollen, müssen wir nur den vorherigen Ausdruck lösen.

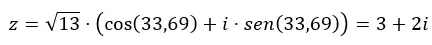
Von der Polarform zur trigonometrischen Form und umgekehrt

Schließlich werden wir von der Polarform zur trigonometrischen Form übergehen. Das ist ganz einfach, denn diese beiden Formen werden durch dieselben zwei Werte ausgedrückt: modulo und argument . Sie müssen also nur noch die Formulare ausfüllen und fertig.

Geben wir ein Beispiel: Wir konvertieren die Zahl z = √85 _12,53 in die trigonometrische Form.

Wir formulieren die beiden Variablen (Modul und Argument) in der Gleichung der trigonometrischen Form um:

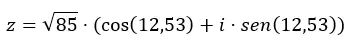
Da Sie nun wissen, wie Sie von einer Form zur anderen wechseln, empfehlen wir Ihnen, mit ein paar Übungen ein wenig zu üben. Auf diese Weise festigen Sie das in diesem Artikel erlernte Wissen. Wenn Sie Fragen zu diesem Thema haben, können Sie diese gerne in den Kommentaren hinterlassen. Und wenn Sie mehr über komplexe Zahlen erfahren möchten, schauen Sie sich die folgenden Links an.