Koordinatensystem

Auf dieser Seite erklären wir, was ein Koordinatensystem ist und außerdem erfahren Sie alles über das kartesische Koordinatensystem. Sie werden auch andere Arten von Koordinatensystemen (polar, zylindrisch, sphärisch usw.) und reale Anwendungen eines Koordinatensystems sehen.

Was ist ein Koordinatensystem?

Obwohl es zunächst etwas schwierig ist, dieses Konzept zu verstehen, lautet die Definition eines Koordinatensystems:

Ein Koordinatensystem ist ein System, das es uns ermöglicht, die Position eines Punktes zu bestimmen. Das heißt, es handelt sich um eine Reihe von Werten, die zur Definition der Position eines beliebigen geometrischen Objekts verwendet werden.

Beispielsweise kann die Position, in der das folgende Flugzeug fliegt, durch ein Koordinatensystem beschrieben werden:

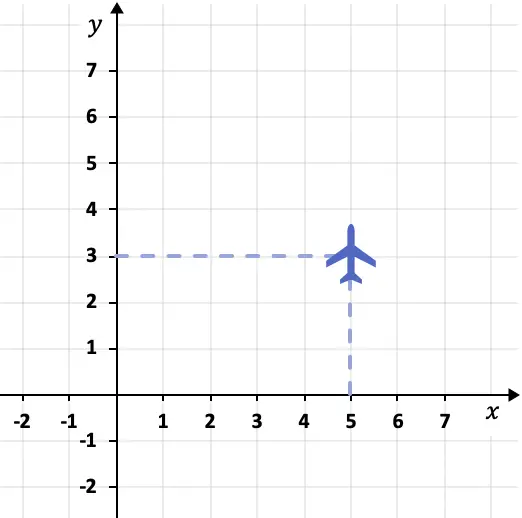
In diesem Fall befindet sich die Ebene im Punkt (5.3). Weil seine X-Koordinate 5 und seine Y-Koordinate 3 ist.

Andererseits wird der Punkt (0,0) als Koordinatenursprung bezeichnet, da dort die Koordinatenachsen beginnen und er der Bezugspunkt des Koordinatensystems ist.

Aus Neugier geht man davon aus, dass der Mathematiker, der das Koordinatensystem erfunden hat, der Franzose René Descartes war. Deshalb wird es auch das kartesische Koordinatensystem genannt.

Kartesisches Koordinatensystem in der Ebene

Der Graph, den wir im vorherigen Abschnitt gesehen haben, gehört zum kartesischen Koordinatensystem in der Ebene. Wir sagen, dass es sich in der Ebene befindet, weil es ein zweidimensionales System ist, das heißt, dass es nur zwei Achsen hat: die X-Achse und die Y-Achse.

Die X-Achse entspricht horizontalen Koordinaten, während die Y-Achse vertikale Koordinaten darstellt. Nachfolgend sehen Sie mehrere Punkte grafisch dargestellt mit ihren Koordinaten:

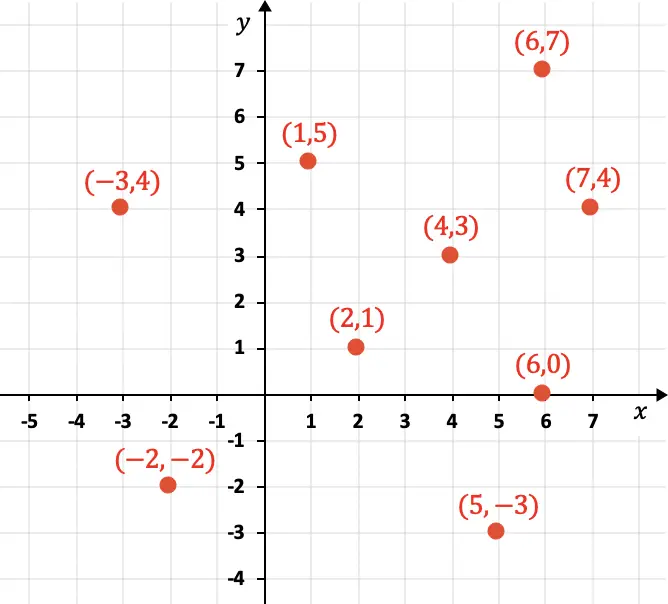
Wie Sie in der Grafik sehen können, werden die Koordinaten numerisch mit Klammern dargestellt, außerdem wird zuerst die X-Komponente und dann die Y-Komponente gesetzt: (4,3). Darüber hinaus können Koordinaten positiv, negativ oder Null sein.

Andererseits wird diese Art von Koordinatensystem auch als kartesische Ebene bezeichnet.

Schließlich sollten Sie wissen, dass Koordinatenachsen auf verschiedene Arten ausgedrückt werden können, obwohl sie alle dasselbe bedeuten:

• Die X-Achse wird auch Abszissenachse oder OX-Achse genannt.
• Die Y-Achse wird auch y-Achse oder OY-Achse genannt.

Kartesisches Koordinatensystem im Raum

Wir haben gerade gesehen, wie man einen Punkt in der Ebene darstellt, also in einem Koordinatensystem mit zwei Achsen (2 Dimensionen). Die Realität besteht jedoch aus 3 Dimensionen (Höhe, Breite und Tiefe).

Daher wird in der euklidischen Geometrie der dreidimensionale Raum im Allgemeinen durch ein Koordinatensystem mit drei Achsen dargestellt, die alle senkrecht zueinander stehen:

• Die X-Achse stellt die Tiefe dar.
• Die Y-Achse gibt die Breite an.
• Die Z-Achse entspricht der Höhe.

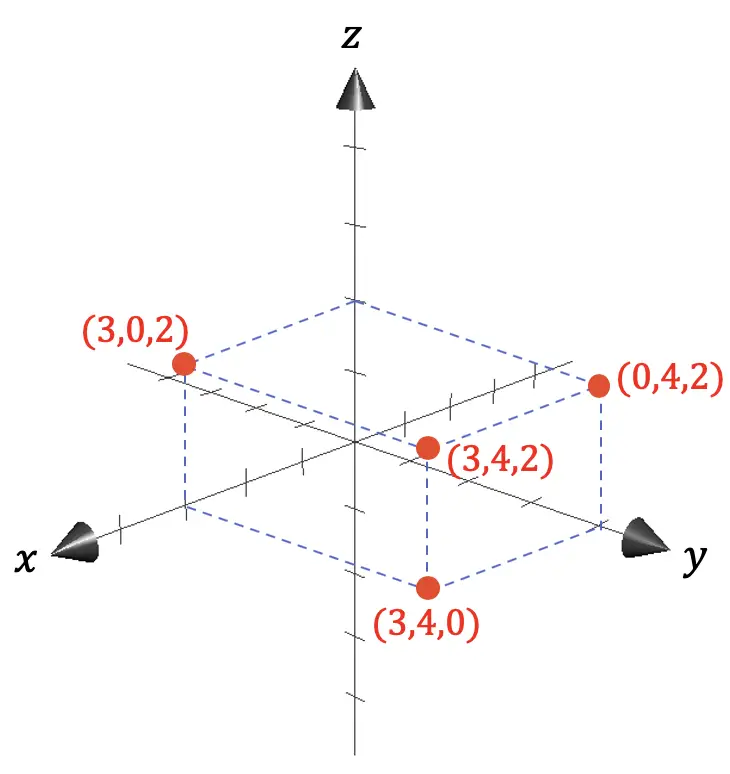
Wie Sie in der vorherigen grafischen Darstellung sehen können, ergeben sich die Koordinaten eines beliebigen Punktes aus den Projektionen der Abstände zwischen dem betreffenden Punkt und dem Ursprung (0,0,0) auf die Achsen.

Polarkoordinatensystem

Am häufigsten werden kartesische Koordinatensysteme (2D oder 3D) verwendet. In manchen Fällen kann es für uns jedoch praktisch sein, eine andere Art von Koordinatensystem zu verwenden.

Das Polarkoordinatensystem ist ein zweidimensionales Bezugssystem, dessen Koordinaten sind:

• 

  ist der Abstand zwischen dem Koordinatenursprung und dem Punkt. Dies wird als Radialkoordinate bezeichnet.

• 

  ist der Winkel, den die X-Achse mit der Linie bildet, die durch den Punkt und den Ursprung verläuft. Dies wird als Winkel- oder Azimutkoordinate bezeichnet.

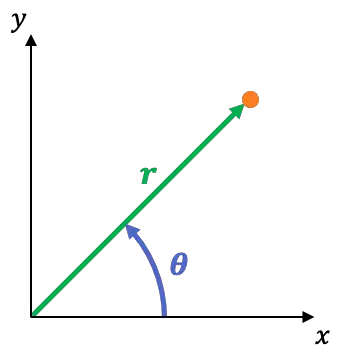
Mithilfe der folgenden Gleichungen können Sie ganz einfach vom rechtwinkligen Koordinatensystem zum Polarkoordinatensystem wechseln:

Zylindrisches Koordinatensystem

Das Zylinderkoordinatensystem ist dem Polarkoordinatensystem sehr ähnlich. Tatsächlich ist es dasselbe, aber mit einer weiteren Koordinate: der Höhe.

Der zylindrische Rahmen ist also ein dreidimensionaler Rahmen, also mit 3 Koordinaten:

• 

  ist die orthogonale Projektion des Punktes in der XY-Ebene, oder mit anderen Worten, der Abstand des Punktes von der Z-Achse.

• 

  ist der Winkel, den die positive Halbachse hat

  

• 

  ist die Höhe des Punktes, ist die gleiche Koordinate des kartesischen Koordinatensystems im Raum.

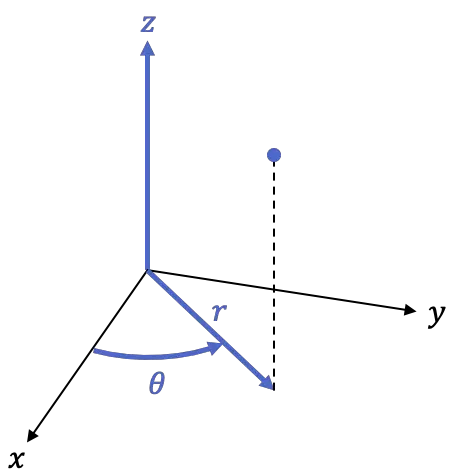
Zur Umrechnung des kartesischen Koordinatensystems in Zylinderkoordinaten werden folgende Formeln verwendet:

Sphärisches Koordinatensystem

Schließlich haben wir das sphärische Koordinatensystem. Diese Art von Koordinatensystem ist auch Polarkoordinaten und Zylinderkoordinaten recht ähnlich, obwohl es offensichtlich einige Unterschiede zu ihnen aufweist.

Das sphärische Koordinatensystem ist ein System zur Beschreibung dreidimensionaler euklidischer Räume und hat daher drei Koordinaten:

• 

  ist der Abstand (in R3) vom Ursprung zum Punkt.

• 

  ist der Winkel, den der positive Teil der X-Achse mit der Linie bildet

  

  in die XY-Ebene projiziert.

• 

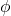
  ist der Winkel zwischen dem positiven Teil der Z-Achse und der Linie

  

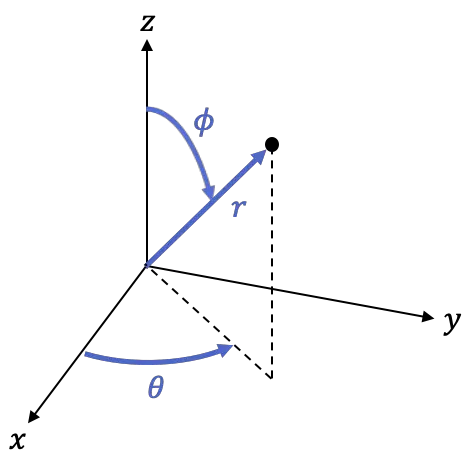
Mit den folgenden Formeln können Sie zwischen sphärischen und kartesischen Koordinaten wechseln:

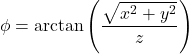
Reale Anwendungen des Koordinatensystems

Koordinatensysteme sind in der Mathematik deshalb so wichtig, weil sie auch im wirklichen Leben verwendet werden. Sie sind beispielsweise nützlich, um Objekte, Personen oder sogar Orte auf einer Karte zu lokalisieren. Tatsächlich existiert GPS aufgrund von Koordinatensystemen, da sie diese nutzen, um Ihre Position auf der Erde zu ermitteln.

Genauer gesagt bestehen geografische GPS-Koordinaten aus zwei Elementen: Breitengrad und Längengrad. Breitengrad (Norden oder Süden) und Längengrad (Osten oder Westen) sind zwei Winkelkoordinaten, die den Winkel zwischen dem Erdmittelpunkt und Ihrem Standort messen. Beide werden in Grad ausgedrückt, entweder in Dezimal- oder Sexagesimalkoordinaten.