Hier finden Sie die Erklärung der Formel für die kanonische (oder segmentale) Gleichung der Geraden, auch symmetrische Gleichung genannt. Darüber hinaus haben Sie die Möglichkeit, Beispiele zu sehen und mit gelösten Übungen zu üben. Und sogar erfahren Sie, wie die kanonische Gleichung aus der allgemeinen (oder impliziten) Gleichung der Geraden berechnet wird.
Wie lautet die kanonische oder segmentale Gleichung der Geraden?
Denken Sie daran, dass die mathematische Definition einer Linie eine Menge aufeinanderfolgender Punkte ist, die in derselben Richtung ohne Kurven oder Winkel dargestellt werden.
Somit ist die kanonische Geradengleichung , auch Segmentgleichung der Geraden genannt, eine Möglichkeit, jede Gerade mathematisch auszudrücken. Dazu genügt es, die Schnittpunkte mit den Koordinatenachsen dieser Geraden zu kennen.
Andererseits wird in der analytischen Geometrie die kanonische (oder segmentale) Gleichung der Linie auch als symmetrische Gleichung der Linie bezeichnet.
Formel der kanonischen oder segmentalen Gleichung der Geraden
Die kanonische oder Segmentgleichung der Linie ist der algebraische Ausdruck der Linie, der bestimmt werden kann, indem man die Werte kennt, an denen die Linie die x-Achse und die y-Achse schneidet.
Wenn eine Gerade die kartesischen Achsen an folgenden Punkten schneidet:
Schnittpunkt mit der X-Achse:
![]()
Schnittpunkt mit der Y-Achse:
![]()
Die Formel für die kanonische (oder segmentale) Gleichung der Geraden lautet:
![]()

Es ist zu beachten, dass es in keinem der folgenden drei Fälle eine kanonische (oder segmentale) Gleichung der Geraden gibt:
- Wenn die Linie vertikal ist, also parallel zur OY-Achse. Weil die Gleichung einer vertikalen Linie lautet

- Wenn die Linie horizontal ist, also parallel zur OX-Achse. Denn die Gleichung einer horizontalen Linie lautet

- Wenn die Linie durch den Koordinatenursprung (Punkt) verläuft
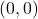
), da wir dann zwei Unbestimmtheiten in der Geradengleichung hätten.
Beispiel, wie man die kanonische oder segmentale Gleichung der Geraden findet
Damit Sie das Konzept besser verstehen, lösen wir ein segmentales (oder kanonisches) Gleichungsproblem der Geraden:
- Finden Sie die kanonische oder segmentale Gleichung der Geraden, die durch die folgenden zwei Punkte verläuft:
![]()
In diesem Fall liefert uns die Deklaration nicht 2 Punkte, sondern die beiden Schnittpunkte mit den Achsen.
Schnittpunkt der Geraden mit der X-Achse:
![]()
Schnittpunkt der Linie mit der Y-Achse:
![]()
Da wir also bereits die beiden Schnittpunkte mit den Achsen kennen, müssen wir nur noch die Formel für die kanonische oder Segmentgleichung der Geraden anwenden:
![]()
Und schließlich ersetzen wir die Werte der Parameter
![]()
Und
![]()
in der Formel:
![]()
Sie wissen jetzt, wie die kanonische (oder segmentale) Gleichung der Geraden lautet. Sie sollten jedoch wissen, dass es andere Möglichkeiten gibt, eine Linie auszudrücken, und unter diesen sticht die explizite Gleichung hervor. Diese Art von Geradengleichung ist schwer vollständig zu verstehen, daher haben wir auf der verlinkten Seite alles dazu ausführlich erklärt.
Berechnen Sie die kanonische oder Segmentgleichung der Geraden aus ihrer allgemeinen Gleichung
Wir haben gerade eine Möglichkeit gesehen, die kanonische oder segmentale Gleichung der Geraden zu bestimmen, es gibt aber auch andere Methoden:
Die kanonische oder Segmentgleichung einer Geraden kann aus der allgemeinen (oder impliziten) Gleichung dieser Geraden ermittelt werden:
![]()
Zuerst wechseln wir die Seite beim Koeffizienten C:
![]()
Als nächstes dividieren wir die gesamte Gleichung durch den Wert des vorzeichengeänderten Parameters C:
![]()
![]()
Und durch die Eigenschaften von Brüchen gelangen wir zur Formel für die kanonische oder Segmentgleichung der Geraden:
![]()
Aus dieser Formel folgt also, dass die Terme
![]()
Und
![]()
der kanonischen Gleichung einer Geraden entsprechen den folgenden Ausdrücken:
![]()
Probleme der kanonischen oder segmentalen Geradengleichung gelöst
Übung 1
Was sind die Schnittpunkte mit den Koordinatenachsen der folgenden Geraden?
![]()
Die Linie in der Übung wird in Form einer kanonischen oder Segmentgleichung der Linie ausgedrückt, deren Formel lautet:
![]()
Daher sind die Punkte, an denen die Linie die Koordinatenachsen schneidet:
Schnittpunkt mit der X-Achse:
![]()
Schnittpunkt mit der Y-Achse:
![]()
Übung 2
Was ist die kanonische oder segmentale Gleichung der dargestellten Linie?
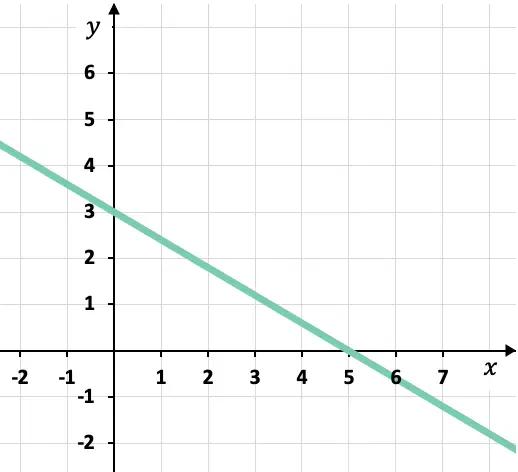
Aus dem Diagramm können wir die Punkte erkennen, an denen die Linie die Koordinatenachsen schneidet:
Schnittpunkt der Geraden mit der X-Achse:
![]()
Schnittpunkt der Linie mit der Y-Achse:
![]()
Sobald wir also bereits die beiden Schnittpunkte mit den Achsen kennen, müssen wir nur noch die Formel für die kanonische oder Segmentgleichung der Geraden verwenden:
![]()
Und schließlich ersetzen wir die Werte der Parameter
![]()
Und
![]()
in der Formel:
![]()
Übung 3
Berechnen Sie die kanonische oder segmentale Gleichung der Linie, die durch die folgende allgemeine (oder implizite) Gleichung bestimmt wird:
![]()
Um von einer allgemeinen Gleichung zu einer Segmentgleichung zu gelangen, müssen wir zunächst den unabhängigen Term der Gleichung isolieren:
![]()
![]()
Zweitens dividieren wir die gesamte Gleichung durch den Koeffizienten auf der rechten Seite der Gleichung:
![]()
![]()
Der obige Ausdruck entspricht dem folgenden:
![]()
Damit lautet die kanonische, segmentale oder symmetrische Gleichung der Geraden:
![]()
Übung 4
Bestimmen Sie die kanonische oder segmentale Gleichung, deren Richtungsvektor ist
![]()
und geht durch den Punkt
![]()
Wir finden zunächst leicht die stetige Gleichung der Geraden aus ihrem Richtungsvektor und einem Punkt, der zur Geraden gehört:
![]()
![]()
![]()
Berechnen wir nun die allgemeine Geradengleichung, indem wir die Brüche kreuzweise multiplizieren und die resultierenden Terme gruppieren:
![]()
![]()
![]()
![]()
Es genügt daher, die allgemeine Geradengleichung in eine kanonische Gleichung umzuwandeln. Dazu löschen wir zunächst den unabhängigen Term aus der Gleichung:
![]()
Als nächstes dividieren wir die gesamte Gleichung durch den Koeffizienten auf der rechten Seite der Gleichung:
![]()
![]()
Der obige Ausdruck entspricht dem folgenden:
![]()
Negativ geteilt durch Negativ ergibt positiv:
![]()
Brüche können nicht weiter vereinfacht werden, daher lautet die kanonische, segmentale oder symmetrische Gleichung der Geraden:
![]()