Jacobi- und Jacobi-Matrix

Auf dieser Seite erfahren Sie, was die Jacobi-Matrix ist und wie Sie sie anhand eines Beispiels berechnen. Darüber hinaus stehen Ihnen mehrere gelöste Übungen zu Jacobi-Matrizen zum Üben zur Verfügung. Sie werden auch sehen, warum die Determinante der Jacobi-Matrix, die Jacobi-Matrix, so wichtig ist. Abschließend erläutern wir die Beziehungen, die diese Matrix zu anderen Vorgängen und den darin enthaltenen Anwendungen unterhält.

Was ist die Jacobi-Matrix?

Die Definition der Jacobi-Matrix lautet wie folgt:

Die Jacobi-Matrix ist eine Matrix, die durch partielle Ableitungen erster Ordnung einer Funktion gebildet wird.

Die Formel für die Jacobi-Matrix lautet daher wie folgt:

Daher haben Jacobi-Matrizen immer so viele Zeilen wie Skalarfunktionen

$(f_1,f_2,\ldots ,f_m)$

haben die Funktion und die Anzahl der Spalten entspricht der Anzahl der Variablen

$(x_1, x_2, \ldots , x_n).$

Andererseits wird diese Matrix auch als Jacobi-Differenzialkarte oder Jacobi-Linearkarte bezeichnet. Tatsächlich wird es manchmal auch mit dem Buchstaben D statt mit dem Buchstaben J geschrieben:

$\displaystyle J_f = D_f$

Kurioserweise ist die Jacobi-Matrix nach Carl Gustav Jacobi benannt, einem bedeutenden Mathematiker und Professor des 19. Jahrhunderts, der wichtige Beiträge zur Welt der Mathematik leistete, insbesondere auf dem Gebiet der linearen Algebra.

Beispiel für die Berechnung der Jacobi-Matrix

Sobald wir das Konzept der Jacobi-Matrix kennengelernt haben, werden wir anhand eines Beispiels Schritt für Schritt sehen, wie sie berechnet wird:

Bestimmen Sie die Jacobi-Matrix am Punkt (1,2) der folgenden Funktion:

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

Als Erstes müssen wir alle partiellen Ableitungen erster Ordnung der Funktion berechnen:

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

Jetzt wenden wir die Jacobi-Matrixformel an. In diesem Fall hat die Funktion zwei Variablen und zwei Skalarfunktionen, sodass die Jacobi-Matrix eine quadratische Matrix der Dimension 2×2 ist:

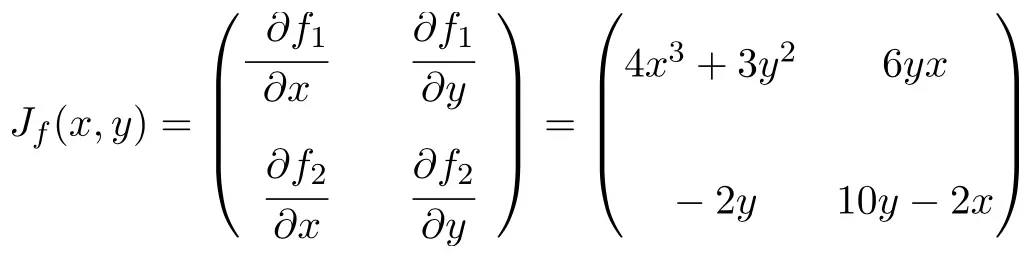
Sobald wir den Ausdruck für die Jacobi-Matrix haben, werten wir ihn bei Punkt (1,2) aus:

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

Und schließlich führen wir die Operationen durch und erhalten die Lösung:

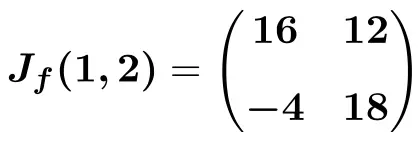
Beispiel für die Berechnung der Jacobi-Matrix

Sobald Sie gesehen haben, wie Sie die Jacobi-Matrix einer Funktion finden, überlassen wir Ihnen einige Übungen, die Schritt für Schritt gelöst werden, damit Sie üben können.

Probleme von Jacobi-Matrizen gelöst

Übung 1

Finden Sie die Jacobi-Matrix am Punkt (0,-2) der folgenden Vektorfunktion in 2 Variablen:

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

siehe Lösung

Die Funktion hat zwei Variablen und zwei Skalarfunktionen, sodass die Jacobi-Matrix eine quadratische Matrix der Größe 2×2 ist:

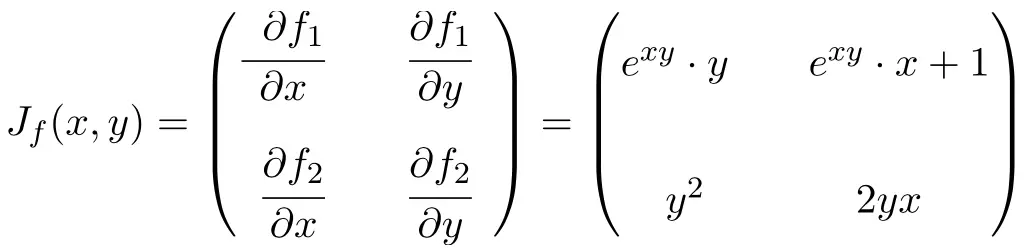
Nachdem wir den Ausdruck für die Jacobi-Matrix berechnet haben, werten wir ihn am Punkt (0,-2) aus:

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

Und schließlich führen wir die Operationen durch und erhalten das Ergebnis:

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

Übung 2

Berechnen Sie die Jacobi-Matrix am Punkt (2,-1) der folgenden Funktion mit 2 Variablen:

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

siehe Lösung

In diesem Fall hat die Funktion zwei Variablen und zwei Skalarfunktionen, sodass die Jacobi-Matrix eine quadratische Matrix der Ordnung 2 ist:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

Sobald wir den Ausdruck für die Jacobi-Matrix gefunden haben, werten wir ihn bei Punkt (2,-1) aus:

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

Und schließlich führen wir die Operationen durch und erhalten das Ergebnis:

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

Übung 3

Bestimmen Sie die Jacobi-Matrix am Punkt (2,-2,2) der folgenden Funktion mit 3 Variablen:

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

siehe Lösung

In diesem Fall hat die Funktion drei Variablen und zwei Skalarfunktionen, daher ist die Jacobi-Matrix eine rechteckige Matrix der Dimension 2×3:

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

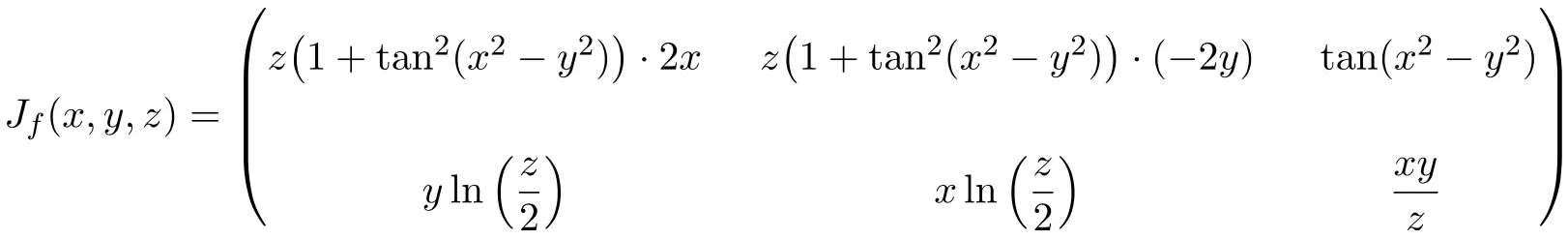
Jacobi-Matrix gelöste Aufgabe von 3 Variablen

Sobald wir den Ausdruck für die Jacobi-Matrix haben, werten wir ihn am Punkt (2,-2,2) aus:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

Wir führen die Berechnungen durch:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

Und wir machen weiter, bis es nicht mehr vereinfacht werden kann:

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

Übung 4

Bestimmen Sie die Jacobi-Matrix an diesem Punkt

$(\pi, \pi)$

der folgenden multivariablen Funktion:

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

siehe Lösung

In diesem Fall hat die Funktion zwei Variablen und drei Skalarfunktionen, daher ist die Jacobi-Matrix eine rechteckige Matrix der Dimension 3×2:

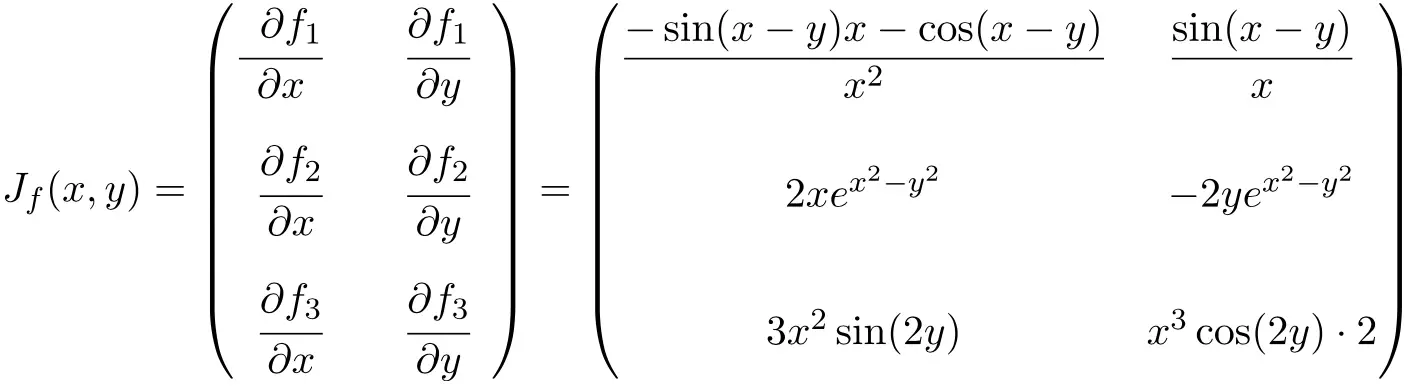
Übung Schritt für Schritt zur Jacobi-Matrix gelöst

Sobald wir den Ausdruck für die Jacobi-Matrix haben, werten wir ihn auf den Punkt aus

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

Wir führen die Operationen durch:

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

Somit hat die Jacobi-Matrix der Vektorfunktion am betrachteten Punkt den Wert:

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

Übung 5

Berechnen Sie die Jacobi-Matrix an diesem Punkt

$(3,0,\pi)$

der folgenden Funktion mit 3 Variablen:

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

siehe Lösung

In diesem Fall besteht die Funktion aus drei Variablen und drei Skalarfunktionen, daher ist die Jacobi-Matrix eine quadratische Matrix der Dimension 3×3:

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

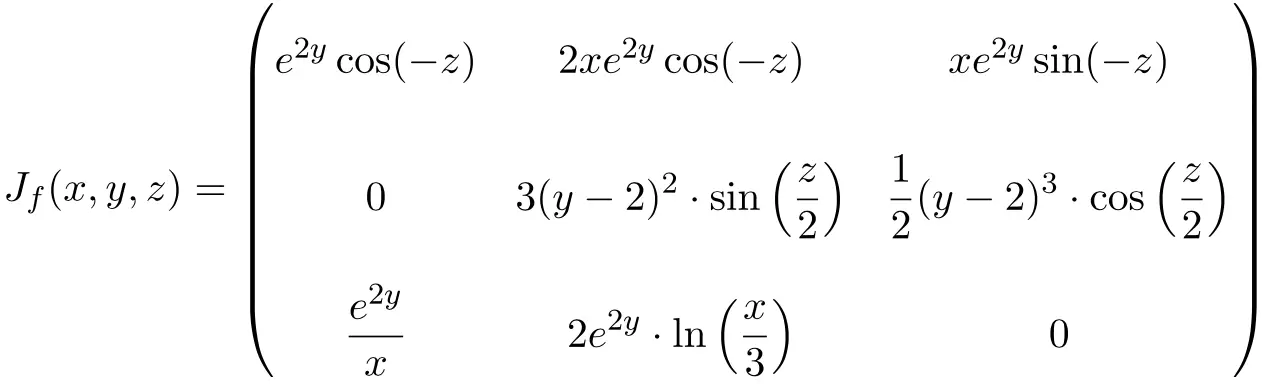
Gelöste Übung einer 3x3-Jacobian-Matrix mit 3 Variablen

Sobald wir die Jacobi-Matrix gefunden haben, werten wir sie an diesem Punkt aus

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

Wir berechnen die Operationen:

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

Und das Ergebnis der Jacobi-Matrix an diesem Punkt ist:

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

Determinante der Jacobi-Matrix: die Jacobi-Matrix

Die Determinante der Jacobi-Matrix wird Jacobi- Determinante oder Jacobi-Matrix genannt. Es muss berücksichtigt werden, dass die Jacobi-Matrix nur berechnet werden kann, wenn die Funktion die gleiche Anzahl an Variablen wie die Skalarfunktionen hat, da die Jacobi-Matrix dann die gleiche Anzahl an Zeilen wie Spalten hat und daher ein Quadrat ist Matrix. .

Jacobi-Beispiel

Sehen wir uns ein Beispiel für die Berechnung der Jacobi-Determinante einer Funktion mit zwei Variablen an:

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

Wir berechnen zunächst die Jacobi-Matrix der Funktion:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

Und jetzt lösen wir die Determinante der 2×2-Matrix:

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

Die Jacobi-Funktion und die Umkehrbarkeit einer Funktion

Nachdem Sie nun das Konzept des Jakobianers kennengelernt haben, haben Sie sich wahrscheinlich gefragt: Nun, was ist der Sinn?

Nun, die Hauptanwendung des Jacobi-Algorithmus besteht darin, zu bestimmen, ob eine Funktion umgekehrt werden kann. Der Umkehrfunktionssatz besagt, dass, wenn die Determinante der Jacobi-Matrix (die Jacobi-Matrix) von 0 verschieden ist, dies bedeutet, dass diese Funktion invertierbar ist.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

Es ist zu beachten, dass diese Bedingung notwendig, aber nicht ausreichend ist. Das heißt, wenn die Determinante ungleich Null ist, können wir behaupten, dass die Matrix invertiert werden kann. Wenn die Determinante jedoch 0 ist, können wir nicht wissen, ob die Funktion hat eine Umkehrung oder Nr.

In dem zuvor gezeigten Beispiel, wie man die Jacobi-Funktion einer Funktion ermittelt, gibt beispielsweise die Determinante an

$4x^2+4y^2$

. In diesem Fall können wir behaupten, dass die Funktion immer umgekehrt werden kann, außer am Punkt (0,0), da dieser Punkt der einzige ist, an dem die Jacobi-Determinante gleich Null ist und wir daher nicht wissen, ob die Umkehrfunktion vorliegt existiert in diesem Punkt.

Beziehung der Jacobi-Matrix zu anderen Operationen

Die Jacobi-Matrix hängt mit dem Gradienten und der Hesse-Matrix einer Funktion zusammen:

Neigung

Wenn die Funktion eine Skalarfunktion ist, ist die Jacobi-Matrix eine Zeilenmatrix, die dem Gradienten entspricht:

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

Hessische Matrix

Die Jacobi-Matrix des Gradienten einer Funktion ist gleich der Hesse-Matrix :

$\displaystyle H_f = J(\nabla f)$

Die Hesse-Matrix ist eine sehr wichtige Matrix für die Ableitung von Funktionen mit mehr als einer Variablen, da sie durch die zweiten Ableitungen der Funktion gebildet wird. Tatsächlich könnte man sagen, dass die Hesse-Matrix die Kontinuität der Jacobi-Matrix ist. Aber es ist so wichtig, dass wir eine ganze Seite haben, die es im Detail erklärt. Wenn Sie also genau wissen möchten, was diese Matrix ist und warum sie so besonders ist, können Sie auf den Link klicken.

Anwendungen der Jacobi-Matrix

Neben der Nützlichkeit, die wir von der Jacobi-Matrix gesehen haben, die bestimmt, ob eine Funktion invertierbar ist, hat die Jacobi-Matrix noch andere Anwendungen.

Mithilfe der Jacobi-Matrix werden die kritischen Punkte einer multivariaten Funktion berechnet, die dann über die Hessische Matrix in Maxima, Minima oder Sattelpunkte klassifiziert werden. Um die kritischen Punkte zu finden, müssen Sie die Jacobi-Matrix der Funktion berechnen, sie auf 0 setzen und die resultierenden Gleichungen lösen.

$\displaystyle J_f(x)=0$

Darüber hinaus findet sich eine weitere Anwendung der Jacobi-Matrix in der Integration von Funktionen mit mehr als einer Variablen, also in Doppel-, Dreifachintegralen usw. Da die Determinante der Jacobi-Matrix eine Variablenänderung in mehreren Integralen gemäß der folgenden Formel ermöglicht:

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

Dabei ist T die Variablenänderungsfunktion, die die ursprünglichen Variablen mit den neuen verknüpft.

Schließlich wird die Jacobi-Matrix auch verwendet, um eine lineare Näherung für jede Funktion vorzunehmen

$f$

um einen Punkt

$p$

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

Jacobi- und jacobi-matrix

Was ist die Jacobi-Matrix?

Beispiel für die Berechnung der Jacobi-Matrix

Probleme von Jacobi-Matrizen gelöst

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Determinante der Jacobi-Matrix: die Jacobi-Matrix

Jacobi-Beispiel

Die Jacobi-Funktion und die Umkehrbarkeit einer Funktion

Beziehung der Jacobi-Matrix zu anderen Operationen

Neigung

Hessische Matrix

Anwendungen der Jacobi-Matrix

Kommentar verfassen Kommentieren abbrechen