Involutionsmatrix - Mathematik

Auf dieser Seite erfahren Sie, was eine involutierende Matrix ist. Wir zeigen Ihnen auch Beispiele für involutive Matrizen der Dimensionen 2×2, 3×3 und 4×4. Und schließlich finden Sie die Formel für eine Involutionsmatrix.

Was ist eine Involutionsmatrix?

Die Bedeutung der Involutionsmatrix ist wie folgt:

Definition einer involutiven Matrix : Eine invertierbare quadratische Matrix, deren inverse Matrix die Matrix selbst ist.

$A^{-1} = A$

Gold

$A$

ist eine beliebige Matrix und

$A^{-1}$

stellt seine Umkehrung dar.

Eine Involutionsmatrix ist also offensichtlich ein Beispiel für eine reguläre oder nicht entartete Matrix .

Wenn Sie nicht wissen, was die Inverse einer Matrix ist, können Sie hier sehen, wie Sie die 3×3-Inverse-Matrix berechnen. Es ist wichtig zu wissen, wie man eine Matrix invertiert. Dazu müssen Sie jedoch auch wissen, wie der Adjungierte einer Matrix berechnet wird.

Aber zurück zum Thema: Wenn eine Matrix involutiv ist, ergibt die Multiplikation der Matrix mit der Matrix selbst die Identitätsmatrix. Schauen Sie sich die Demo an:

Jede mit ihrer Umkehrung multiplizierte Matrix ergibt die Identitäts- (oder Einheits-)Matrix. ALSO:

$\displaystyle A \cdot A^{-1} = I$

Und da die Umkehrung einer Involutionsmatrix die Matrix selbst ist:

$\displaystyle A \cdot A = I$

Folglich ergibt eine quadratische Involutionsmatrix die Identitätsmatrix:

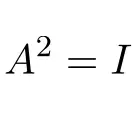
Beispiele für Involutionsmatrizen

Beispiel einer 2×2-Evolventenmatrix:

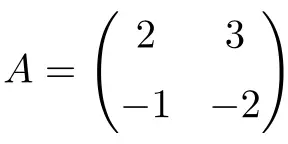
Beispiel einer involutiven Matrix der Dimension 2x2

Wir können überprüfen, ob es sich um eine Involutionsmatrix handelt, indem wir die zweite Potenz der Matrix berechnen:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Da die quadratische Matrix A die Identitätsmatrix ist, ist Matrix A eine 2×2-Involutionsmatrix.

Beispiel einer 3×3-Evolventenmatrix:

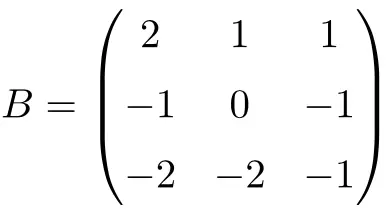
Beispiel einer involutiven Matrix der Dimension 3x3

Wir können überprüfen, ob es sich um eine Involutionsmatrix handelt, indem wir das Produkt der Matrix selbst lösen:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Da die quadratische Matrix B die Identitätsmatrix ist, ist Matrix B eine 3×3-Involutionsmatrix.

Beispiel einer 4×4-Evolventenmatrix:

Die Identitäts- (oder Einheits-)Matrix ist, unabhängig von ihrer Dimension, per Definition eine Involutionsmatrix.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Wir können überprüfen, ob es sich um eine Involutionsmatrix handelt, indem wir die Matrix auf 2 erhöhen:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Da die quadratische Identitätsmatrix die Identitätsmatrix ist, ist die Identitätsmatrix eine 4 × 4-Involutionsmatrix.

Offensichtlich kann die Identitätsmatrix jede Dimension haben, da es sich einfach um eine Diagonalmatrix handelt, bei der alle Einsen auf der Hauptdiagonale liegen und der Rest 0 ist. Die Identitätsmatrix wird also immer eine Involutionsmatrix sein, unabhängig von ihrer Reihenfolge.

Involvierende Matrixformel

Eine der Eigenschaften der Involutionsmatrix besteht darin, dass ihre Formel bekannt sein kann. Aber der Beweis der Formel für eine Involutionsmatrix zweiter Ordnung ist ziemlich mühsam, deshalb überlassen wir es gleich dem Ergebnis, darauf kommt es wirklich an. Wenn Sie sich mehr für die Demo interessieren, können Sie sie unten in den Kommentaren Schritt für Schritt erklärt sehen.

Die Formel für eine Involutivmatrix der Dimension 2 × 2 lautet wie folgt:

Daher ist jede Matrix, deren Hauptdiagonalwerte entgegengesetzt sind und deren Determinante -1 ist, eine Involutionsmatrix.

Zusätzlich zu den durch diese Formel beschriebenen Matrizen muss jedoch berücksichtigt werden, dass die Identitätsmatrix und ihr Gegenteil auch Involutionsmatrizen der Ordnung 2 sind :

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Eigenschaften einer involvierenden Matrix

Involutionsmatrizen haben die folgenden Eigenschaften:

Die Determinante einer Involutionsmatrix ist immer gleich -1 oder +1.

Es gibt eine Beziehung zwischen Involutionsmatrizen und idempotenten Matrizen : die Matrix
$A$

ist genau dann involutionell, wenn die Matrix

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

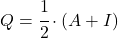
ist idempotent.

Ja
$A$

Und

$B$

sind zwei kommutierende Involutionsmatrizen, dann das Matrixprodukt

$AB$

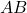
ist auch eine andere Involutionsmatrix.

Jede Potenz einer Involutionsmatrix führt zu einer anderen Involutionsmatrix. Insbesondere ist eine Involutionsmatrix, die auf einen ungeraden Exponenten erhöht wird, sich selbst gleich, wenn sie andererseits auf einen geraden Exponenten erhöht wird, entspricht sie der Identitätsmatrix.

$A^2 = I$

$A^3 = A$