Implizite, allgemeine oder kartesische Gleichung der Ebene

Erläuterung, wie die implizite Ebenengleichung (Formel), auch allgemeine oder kartesische Gleichung genannt, berechnet wird. Darüber hinaus erfahren Sie, wie Sie die Gleichung der Ebene aus ihrem Normalenvektor ermitteln. Darüber hinaus können Sie Beispiele und Übungen Schritt für Schritt lösen sehen.

Was ist die implizite oder allgemeine Gleichung des Plans?

In der analytischen Geometrie ist die implizite Gleichung einer Ebene , auch allgemeine oder kartesische Gleichung der Ebene genannt, eine Gleichung, die es ermöglicht, jede Ebene mathematisch auszudrücken. Um die implizite oder allgemeine Gleichung einer Ebene zu finden, benötigen wir einen Punkt und zwei linear unabhängige Vektoren, die zu dieser Ebene gehören.

Formel der impliziten oder allgemeinen Gleichung des Plans

Betrachten Sie einen Punkt und zwei Richtungsvektoren einer Ebene:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Die implizite, allgemeine oder kartesische Gleichung einer Ebene erhält man, indem man die folgende Determinante löst und das Ergebnis gleich 0 setzt:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Somit lautet die implizite oder allgemeine Gleichung des resultierenden Plans wie folgt:

$Ax+By+Cz+D=0$

Wichtig ist, dass die beiden Vektoren in der Formel linear unabhängig voneinander sind, also unterschiedliche Richtungen haben müssen. Und damit diese Bedingung erfüllt ist, reicht es aus, dass die beiden Vektoren nicht parallel sind.

implizite oder allgemeine oder kartesische Gleichung von pan xy in r3

Obwohl es nicht notwendig ist, den Grund für diese Formel zu kennen, können Sie ihre Demonstration unten sehen.

Ausgehend von den parametrischen Gleichungen eines Plans gehen wir zur impliziten (oder allgemeinen) Gleichung des Plans über:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Zuerst übergeben wir den unabhängigen Term jeder parametrischen Gleichung an die andere Seite der Gleichung:

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Oder gleichwertig:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Damit das obige Gleichungssystem eine zulässige Lösung hat, muss der Rang der folgenden Matrix gleich 2 sein (Theorem von Rouche-Frobenius):

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Wenn also der Bereich der vorherigen Matrix zwei sein muss, muss die 3×3-Determinante notwendigerweise gleich Null sein:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Und indem wir diese Determinante lösen, erhalten wir die allgemeine, implizite oder kartesische Gleichung einer Ebene:

$Ax+By+Cz+D=0$

Wir haben also gerade die implizite (oder allgemeine) Gleichung und die parametrischen Gleichungen der Ebene gesehen, es gibt jedoch noch mehr Möglichkeiten, eine Ebene analytisch auszudrücken, wie zum Beispiel die Vektorgleichung und die kanonische Gleichung. Die Formel und Erklärung aller Gleichungen im Plan finden Sie unter diesem Link.

Beispiel dafür, wie man die implizite oder allgemeine Gleichung der Ebene findet

Sehen wir uns anhand eines Beispiels an, wie man die implizite (oder allgemeine oder kartesische) Gleichung einer Ebene bestimmt:

Finden Sie die implizite oder allgemeine Gleichung der Ebene, die durch den Punkt verläuft
$P(3,1,-1)$

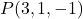
und enthält die Vektoren

$\vv{\text{u}}=(2,0,3)$

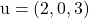
Und

$\vv{\text{v}}=(4,-1,2).$

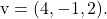
Um die allgemeine oder implizite Gleichung der Ebene zu berechnen, muss die folgende Determinante gelöst werden, die aus den beiden Vektoren, den Variablen und den Koordinaten des Punktes besteht:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Also ersetzen wir die Vektoren und den Punkt in der Formel:

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

Und nun lösen wir die Determinante der Ordnung 3, zum Beispiel mit der Sarrus-Regel oder durch Cofaktoren (oder Stellvertreter):

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Nun operieren und gruppieren wir die Begriffe:

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Daher lautet die implizite oder allgemeine Gleichung des Plans:

$\bm{3x+8y-2z-19 = 0}$

Berechnen Sie die implizite oder allgemeine Gleichung einer Ebene aus ihrem Normalenvektor

Ein sehr typisches Problem bei Gleichungen einer Ebene besteht darin, herauszufinden, wie die Gleichung einer bestimmten Ebene angesichts eines Punktes und seines Normalen- (oder Senkrechten) Vektors aussieht. Schauen wir uns also an, wie es funktioniert.

Aber Sie müssen zunächst wissen, dass die Komponenten X, Y, Z des Vektors normal zu einer Ebene jeweils mit den Koeffizienten A, B, C der impliziten (oder allgemeinen) Gleichung dieser Ebene übereinstimmen.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Gold

$\vv{n}$

ist der Vektor orthogonal zur Ebene

$\pi.$

Sobald wir die vorherige Beziehung kennen, sehen wir uns ein Beispiel für die Lösung dieser Art von Ebenengleichungsproblemen an:

Bestimmen Sie die implizite oder allgemeine Gleichung der Ebene, die durch den Punkt verläuft
$P(1,0,-2)$

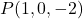
und einer seiner Normalenvektoren ist

$\vv{n}=(3,-1,2) .$

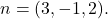
Die Formel für die implizite, allgemeine oder kartesische Gleichung einer Ebene lautet:

$Ax+By+Cz+D=0$

Aus dem Normalenvektor können wir also die Koeffizienten A, B und C ermitteln, da sie den Komponenten seines Normalenvektors entsprechen:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Dabei müssen wir nur den Parameter D finden. Dazu setzen wir die Koordinaten des Punktes, der zur Ebene gehört, in die Gleichung ein:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

Die implizite oder allgemeine Gleichung des Plans lautet also:

$\bm{3x-y+2z+1 = 0}$

Probleme der impliziten oder allgemeinen Gleichung der Ebene gelöst

Übung 1

Finden Sie die implizite oder allgemeine Gleichung der Ebene, die durch den Punkt verläuft

$P(-2,1,3)$

und enthält die Vektoren

$\vv{\text{u}}=(4,1,3)$

Und

$\vv{\text{v}}=(5,3,-1).$

siehe Lösung

Um die allgemeine oder implizite Gleichung der Ebene zu berechnen, muss die folgende Determinante gelöst werden, die aus den beiden Vektoren, den drei Variablen und den Koordinaten des Punktes besteht:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Also ersetzen wir die Vektoren und den Punkt in der Formel:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

Und nun lösen wir die Determinante der 3×3-Matrix mit der Methode Ihrer Wahl:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Abschließend führen wir die Operationen durch und gruppieren ähnliche Begriffe:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Die implizite oder allgemeine Gleichung des Plans lautet also:

$\bm{-8x+11y+7z-20 = 0}$

Übung 2

Bestimmen Sie, ob der Punkt

$P(-1,5,-3)$

gehört zu folgendem Plan:

$\pi : \ 2x+y+6z-5=0$

siehe Lösung

Damit der Punkt in der Ebene liegt, muss seine Gleichung überprüft werden. Daher müssen wir die kartesischen Koordinaten des Punktes in die Gleichung der Ebene einsetzen und prüfen, ob die Gleichung erfüllt ist:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

Der Punkt respektiert nicht die Gleichung der Ebene und ist daher nicht Teil dieser Ebene.

Übung 3

Finden Sie die implizite (oder allgemeine) Gleichung des Plans, die die folgenden drei Punkte enthält:

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

siehe Lösung

Um die implizite Gleichung der Ebene zu finden, müssen wir zwei linear unabhängige Vektoren finden, die in der Ebene binden. Und dazu können wir zwei Vektoren berechnen, die durch die 3 Punkte definiert werden:

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

Die Koordinaten der beiden gefundenen Vektoren sind nicht proportional, also praktisch linear unabhängig voneinander.

Da wir nun bereits zwei Richtungsvektoren und einen Punkt der Ebene kennen, können wir bereits die Formel für die allgemeine Gleichung der Ebene anwenden:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Wir setzen die Vektoren und einen der drei Punkte in die Formel ein:

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$