Sie haben sicherlich schon einmal von der Menge der imaginären Zahlen oder der imaginären Einheit gehört. Es handelt sich um ein mathematisches Konzept, das aus der mathematischen Notwendigkeit entsteht, Zahlen auszudrücken, die nicht zu den reellen Zahlen gehören.
Was sind imaginäre Zahlen?
Imaginäre Zahlen sind solche, die quadriert eine negative Zahl ergeben. Daher handelt es sich um Werte, die der Quadratwurzel einer negativen Zahl entsprechen. Beispielsweise ist die imaginäre Einheit (die Zahl i) gleich der Quadratwurzel von -1.
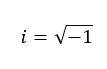
Diese Zahlen gehören nicht zu den reellen Zahlen, da in der reellen Menge negative Wurzeln nicht aufgelöst werden können. Hier liegt die Bedeutung der imaginären Umgebung. Dieser Satz wurde erfunden, um mit negativen Wurzeln umgehen zu können und um alle Gleichungen und quadratischen Probleme lösen zu können, die „keine Lösung haben“, weil sie uns eine negative Wurzel liefern.
Um Verwirrung zu vermeiden, ist es wichtig, zwischen imaginären Zahlen und komplexen Zahlen zu unterscheiden. Komplexe sind Zahlen, die aus einer reellen Zahl und einer imaginären Zahl bestehen. Daher sind Imaginäre eine Unterkategorie von Komplexen, die keinen Realteil haben. In der folgenden Tabelle können Sie die Unterschiede besser erkennen.
| komplexe Zahl | königliche Partei | Fantasieteil | Beschreibung |
| 4+7i | 4 | 7i | Komplex |
| 3 | 3 | 0 | rein königlich |
| 2i | 0 | 2i | Pure Fantasie |
Um die Positionierung dieses digitalen Sets abzuschließen, können wir im folgenden Bild eine Struktur aller Sets visualisieren. Wie wir sehen können, umfassen komplexe Zahlen alle Arten von Zahlen . Diese wiederum können in reelle Zahlen und reine imaginäre Zahlen (mit denen wir uns in diesem Artikel befassen) unterteilt werden.

Beispiele für imaginäre Zahlen
Aus der imaginären Einheit (i) können wir andere imaginäre Zahlen ableiten. Sie müssen lediglich die folgende Formel anwenden:
m = ri
Dabei ist m eine imaginäre Zahl, r eine reelle Zahl und i die imaginäre Einheit. Im folgenden Bild können Sie sehen, wie wir aus negativen Wurzeln unterschiedliche Vorstellungen erhalten.
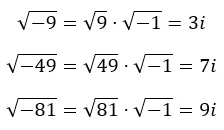
Tatsächlich können wir es auf den folgenden Ausdruck extrapolieren:
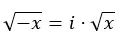
Eigenschaften imaginärer Zahlen
Imaginäre Zahlen haben eine Reihe sehr interessanter Eigenschaften . Über einige haben wir bereits am Anfang dieses Artikels gesprochen, über andere noch nicht:
- Imaginäre gehören nicht zur Menge der Realitäten, da es sich um Zahlen handelt, die physisch nicht existieren und in unserer Realität nicht dargestellt werden können.
- Dies sind Werte, die negativen Wurzeln entsprechen.
- Sie können auf der imaginären Linie grafisch dargestellt werden.
- Imaginäre Potenzen (dieses Konzept werden wir im nächsten Abschnitt erläutern) sind eine große Hilfe bei der Vereinfachung numerischer Berechnungen mit imaginären Werten.
- Die Eulersche Formel ist ein Ausdruck, der es Ihnen ermöglicht, imaginäre Zahlen mit reellen Zahlen in Beziehung zu setzen.
Operationen mit imaginären Zahlen
Nachdem Sie nun alle wichtigen Eigenschaften imaginärer Zahlen kennen, ist es an der Zeit zu lernen, wie man Operationen mit ihnen löst. Um mit imaginären Werten zu arbeiten , müssen Sie die gleichen Schritte befolgen, die Sie für die Arbeit mit realen Werten befolgen, außer dass Sie ein Konzept berücksichtigen müssen: imaginäre Potenzen.
Vorstellungskraft
Imaginäre Zahlen haben eine sehr interessante Eigenschaft, die auftritt, wenn man die imaginäre Einheit mit sich selbst multipliziert. Das heißt, dies geschieht, wenn man Potenzen aus imaginärer Einheit macht. Wenn wir die Potenzen wie in der folgenden Liste aufschreiben, lässt sich ein Muster entdecken:
ich 0 = 1
Ich 1 = Ich
i 2 = i · i = ( √ -1) · ( √ -1) = -1
i 3 = i 2 i = (-1) i = -i
i 4 = i 2 i 2 = (-1) (-1) = 1
Die Kenntnis dieses Konzepts wird es uns viel einfacher machen, Operationen mit imaginären Zahlen zu lösen, da wir in der Lage sein werden, schwierige Operationen zu vereinfachen und ein wenig einfacher zu machen. Das Gute an diesen Kräften ist auch, dass sie sich auf unbestimmte Zeit wiederholen. Das können wir sehen, wenn wir noch ein paar Potenzen hinzufügen:
Ich 5 = Ich
ich 6 = -1
ich 7 = -i
ich 8 = 1
usw.
Und bei negativen Kräften passiert das auch.
Arithmetische Operationen mit imaginären Zahlen
Als nächstes geben wir Ihnen ein Beispiel für jede grundlegende arithmetische Operation, damit Sie sehen können, wie die Berechnungen mit imaginären Zahlen gelöst werden.
- Imaginäre Zahlen addieren: Es ist genau das Gleiche wie das Addieren reeller Zahlen, nur vergessen Sie nicht, das i hinzuzufügen.
4i + 3i = 7i
- Subtraktion imaginärer Zahlen: Auch Subtraktionen werden auf die gleiche Weise gelöst wie in der reellen Menge.
4i – 3i = I
- Multiplikation imaginärer Zahlen: In diesem Fall müssen wir die zuvor erwähnten imaginären Potenzen berücksichtigen.
3i 4i = 12 i 2 = 12 (-1) = -12
- Division imaginärer Zahlen: Bei dieser Art der Division müssen wir auch wachsam sein, falls wir auf eine imaginäre Potenz stoßen, die es uns ermöglicht, die Operation zu vereinfachen.
12i ÷ 4i = 3
Gleichungen mit imaginären Zahlen
Wie bereits erwähnt, erhalten wir beim Lösen von Gleichungen in der realen Menge manchmal negative Wurzeln und die Gleichungen haben daher „keine Lösung“ . Aber jetzt, da wir die Imaginären kennen, können wir diese Gleichungen lösen. Sehen wir uns ein Beispiel an:
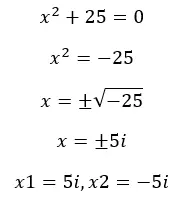
Wofür werden imaginäre Zahlen verwendet?
Imaginäre Zahlen entstehen aus der Notwendigkeit, Werte ausdrücken zu können, die außerhalb der realen Menge liegen. Aus diesem Grund scheint es zunächst so, als hätten sie nicht viele nützliche Anwendungen . Aber die Wahrheit ist, dass es genau das Gegenteil ist. Denn wenn wir sie mit den realen kombinieren, erhalten wir die komplexen Zahlen.
Und diese haben viele Anwendungen. Sie werden zur Untersuchung von Wechselströmen verwendet (da sie negative Werte haben), ihre Verwendung ist auch im Bereich der Wellen (die in der Physik, Telekommunikationselektronik und Quantenmechanik Anwendung finden) weit verbreitet. Neben vielen anderen Verwendungsmöglichkeiten.
Darüber hinaus kommt es häufig vor, dass beim Lösen einer quadratischen Gleichung der Wert eine negative Wurzel ergibt und Sie nicht operieren können … Mit imaginären Gleichungen können Sie sie lösen . Zusammenfassend können wir also sagen, dass es sich um eine Menge handelt, die es uns ermöglicht, unser abstrakteres Wissen zu erweitern.