Hier erfahren Sie, was die Identitätsfunktion ist. Darüber hinaus erfahren Sie, wie Sie die Identitätsfunktion grafisch darstellen und welche Eigenschaften sie hat.
Was ist eine Identitätsfunktion?
Eine Identitätsfunktion ist die Funktion, deren Bild denselben Wert wie das Argument hat. Die Identitätsfunktion kann mit dem Begriff id ausgedrückt werden.
Daher lautet der mathematische Ausdruck für die Identitätsfunktion:
![]()
Zum Beispiel hat das Bild der Identitätsfunktion für x=1 den Wert 1, das Bild von x=2 hat den Wert 2, das Bild von x=3 hat den Wert 3,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
Die Identitätsfunktion ist ein Beispiel für eine lineare Funktion. Unter dem folgenden Link können Sie weitere Beispiele für diese Art von Funktionen sehen:
➤ Siehe: Beispiele für lineare Funktionen
Grafische Darstellung der Identitätsfunktion
Der Graph der Identitätsfunktion entspricht einer Geraden, die die Winkelhalbierende des ersten und dritten Quadranten ist.
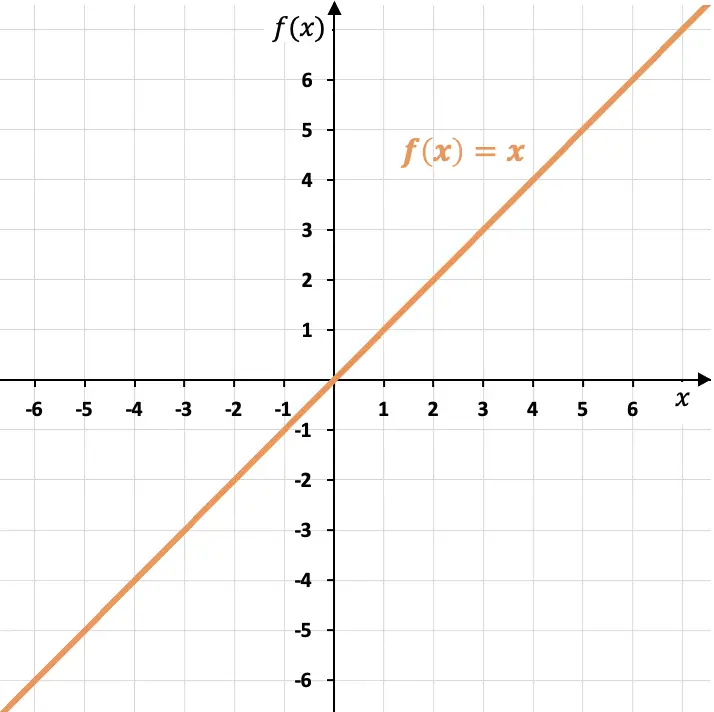
Wie Sie sehen können, verläuft die Identitätsfunktion durch den Koordinatenursprung (Punkt (0,0)) und hat eine Steigung gleich Eins (m=1), da eine Einheit der Variablen zunimmt und für jeden Wert der Unabhängigen Variable X. Zusätzlich bildet die Identitätsfunktion einen Winkel von 45° mit der X-Achse.
Merkmale der Identitätsfunktion
Die Identitätsfunktion hat die folgenden Eigenschaften:
- Der Definitionsbereich der Identitätsfunktion sind alle reellen Zahlen:
![]()
- Der Bereich (oder Bereich) der Identitätsfunktion besteht ebenfalls aus allen reellen Zahlen:
![]()
- Die Identitätsfunktion ist eine stetige und bijektive Funktion.
- Darüber hinaus besteht die Identitätsfunktion aus einer ungeraden Funktion, was bedeutet, dass sie eine symmetrische Funktion in Bezug auf den Koordinatenursprung ist.
![]()
➤ Siehe: ungerade symmetrische Funktion
- Die Identitätsfunktion nimmt über ihren gesamten Bereich zu und ihre Steigung ist gleich 1.
![]()
- Schneidet die x-Achse (OX-Achse) und die y-Achse (Y-Achse) am selben Punkt: dem Koordinatenursprung.
![]()
- Sie kann als Polynomfunktion ersten Grades klassifiziert werden.
- Die Identitätsfunktion fungiert als neutrales Element der Funktionskomposition . Somit ergibt jede mit der Identitätsfunktion zusammengesetzte Funktion die Funktion selbst.
![]()
- Der Wert
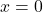
ist die einzige Wurzel dieser Art von Funktion.
- Der Grenzwert der Identitätsfunktion, wenn x gegen plus Unendlich oder minus Unendlich tendiert, ergibt plus Unendlich bzw. minus Unendlich:
![]()
![]()
- Die Identitätsfunktion hat daher keine Asymptote.
- Die Ableitung der Identitätsfunktion ist die konstante Funktion mit dem Wert 1:
![]()
- Das Integral der Identitätsfunktion ist die quadratische Funktion:
![]()
➤ Siehe: Formel für die quadratische Funktion