Identität oder Matrixeinheit

Auf dieser Seite sehen Sie, was die Identitäts- (oder Einheiten-)Matrix ist, sowie mehrere Beispiele. Darüber hinaus erklären wir, welche Eigenschaften die Identitätsmatrix hat, wie man mit dieser Art von Matrix arbeitet und was das Ergebnis ihrer Determinante ist. Schließlich finden Sie die Anwendungen, die diese ganz besondere Matrix hat.

Was ist die Identitätsmatrix?

Die Identitäts- (oder Einheits-)Matrix ist eine quadratische Matrix, die mit Nullen (0) gefüllt ist, außer auf der Hauptdiagonale, wo alle Elemente Einsen (1) sind.

Dies ist die Definition der Identitätsmatrix oder der Einheitsmatrix, aber Sie werden es sicherlich anhand von Beispielen klarer sehen:

Beispiele für Identitätsmatrizen

Beispiel einer Identitätsmatrix der Dimension 2 × 2

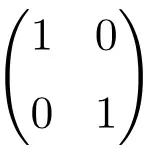
eindeutige Identität oder Matrix der Dimension 2x2

Beispiel einer Identitätsmatrix 3×3-Ordnung

Identität oder eindeutige Matrix der Dimension 3x3

Beispiel einer Identitätsmatrix der Größe 4×4

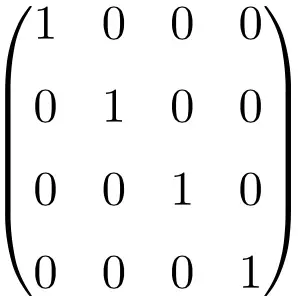
Identität oder eindeutige Matrix der Dimension 4x4

Wie Sie sehen können, müssen wir zum Aufbau der Identitätsmatrix immer noch dem gleichen Verfahren folgen: Setzen Sie Einsen (1) auf die Hauptdiagonale und den Rest alle Nullen (0). Das einzige, was sich ändert, ist die Größe der Tabelle.

Eigenschaften der Identitätstabelle

Die Identitätsmatrix, die Einheitsmatrix oder sogar die identische Matrix werden in der Mathematik häufig verwendet, und das liegt an den Eigenschaften, die diese Art von Matrix besitzt:

Die Identitätsmatrix ist ein Beispiel für eine Diagonalmatrix .

Eine Einheitsmatrix ist sowohl eine obere als auch eine untere Dreiecksmatrix .

Die Identitätsmatrix ist ebenfalls eine symmetrische Matrix .

Der Stellvertreter der Identitätsmatrix ist er selbst.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Es handelt sich um eine invertierbare Matrix. Und was den Adjungierten betrifft, so ist die Umkehrung der Einheitsmatrix selbst:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Jede Skalarmatrix kann durch Multiplikation einer Zahl mit der Identitätsmatrix erhalten werden:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Alle Eigenwerte (oder Eigenwerte) der identischen Matrix sind 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Schließlich ist die Identitätsmatrix auch ein Beispiel für eine Permutationsmatrix .

Operationen mit der Identitäts- (oder Einheiten-)Matrix

Sie denken wahrscheinlich: Das ist alles sehr gut, aber … und wozu dient die Identitätsmatrix? Wenn es nur eine Tabelle mit Nullen und Einsen wäre!

Obwohl Sie dieses Thema vielleicht noch nicht behandelt haben, wird die Identitätsmatrix häufig in der Mathematik verwendet. Tatsächlich ist diese Art von quadratischer Matrix in der linearen Algebra sehr wichtig. Der Hauptnutzen der Identitätsmatrix liegt in der Einfachheit, mit der sie die Berechnung von Matrixoperationen ermöglicht. Sehen wir uns also an, wie man mit der Identitätsmatrix arbeitet:

Addieren und Subtrahieren mit der Identitätsmatrix

Eine Möglichkeit, Zahlen auf der Hauptdiagonalen einer Matrix zu addieren (oder zu subtrahieren), ohne die anderen Elemente zu ändern, besteht darin, die Identitätsmatrix zu verwenden, da sie diesen Zahlen nur eine Einheit hinzufügt (oder subtrahiert). Elemente:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

Sie können den Elementen auf der Diagonale auch weitere Einheiten hinzufügen oder subtrahieren, indem Sie zunächst die Identitätsmatrix mit einem Skalar multiplizieren:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Multiplikation einer Matrix mit der Identitätsmatrix

Bei der Multiplikation einer Matrix mit der Identitätsmatrix fungiert sie als neutrales Element , d. h. jede mit der Identitätsmatrix multiplizierte Matrix ergibt dieselbe Matrix. Schauen Sie sich das folgende Beispiel an:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Darüber hinaus ist die Bedeutung des Matrixprodukts irrelevant, oder mit anderen Worten, es spielt keine Rolle, ob wir die Identitätsmatrix rechts oder links multiplizieren, da das Ergebnis immer dieselbe Matrix sein wird. Um dies zu demonstrieren, wiederholen wir die vorherige Übung, multiplizieren dieses Mal jedoch die Identitätsmatrix mit der entgegengesetzten Seite:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Macht der Identitätsmatrix

Die Potenz der Identitätsmatrix ergibt immer die Identitätsmatrix, unabhängig von dem Exponenten, auf den wir die Matrix erhöhen und der Dimension der Matrix.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Determinante der Identitätsmatrix

Wie Sie sich vermutlich bereits vorstellen können, ist die Determinante der Identitäts- (oder Einheiten-)Matrix immer gleich 1 , unabhängig von der Dimension der Matrix.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Identitätsmatrix-Anwendungen

Schließlich wissen Sie nach all diesen Informationen wahrscheinlich bereits, wie Sie die typische Frage beantworten können: Warum ist die Identitätsmatrix so wichtig? Entspannen Sie sich, diese Frage habe ich mir auch schon einmal gestellt. 😂

Wie Sie bemerkt haben, hat die Identitätsmatrix viele Verwendungsmöglichkeiten und ist deshalb so interessant. Eine der Einsatzmöglichkeiten der Unit-Matrix sind Operationen, denn wie wir gesehen haben, ist es sehr einfach, damit Matrixoperationen durchzuführen.

Andererseits wird die Identitätsmatrix auch zur Lösung von Matrixgleichungen verwendet. Dazu verwenden wir die folgende inverse Matrixeigenschaft: Die Multiplikation einer Matrix mit ihrer inversen Matrix ergibt die Identitätsmatrix. Sie können sehen, wie Sie eine Gleichung mit Matrizen lösen, indem Sie auf den Link klicken.

Darüber hinaus wird die Identitätsmatrix auch zur Berechnung der inversen Matrix mit der Gaußschen Methode verwendet. Bei dieser Methode wird eine Matrix neben der Identitätsmatrix platziert und so eine größere Matrix gebildet. Anschließend muss die ursprüngliche Matrix durch Anwendung elementarer Operationen auf die Zeilen in eine Identitätsmatrix umgewandelt werden. Es scheint sehr kompliziert zu sein, aber in Wirklichkeit ist es nicht so viel, es muss jedoch ein ganzes Verfahren angewendet werden. Wenn Sie also mehr Interesse haben, können Sie in der Suchmaschine der Webseite (oben nach RECHTS) suchen, wie man eine Matrix umkehrt.

Schließlich ist die Identitätsmatrix auch nützlich, um eine Matrix zu diagonalisieren und ihre Eigenwerte (oder Eigenwerte) zu berechnen. Denn durch bestimmte Operationen, in die die Einheitsmatrix eingreift, kann das charakteristische Polynom gewonnen werden, aus dem die Eigenwerte gewonnen werden. Aber es handelt sich bereits um ein sehr fortgeschrittenes Thema, deshalb haben wir eine ganze, sehr umfassende Seite, die der Matrixdiagonalisierung gewidmet ist, mit Beispielen und gelösten Übungen, die es erklären. Wenn Sie mehr Interesse haben, können Sie in unserer Suchmaschine (oben rechts) nach diesem Leitfaden suchen.

Identität oder matrixeinheit