Bemerkenswerte Identitäten (oder bemerkenswerte Produkte) -

Hier finden Sie die Erklärung zur Auflösung aller Arten von bemerkenswerten Identitäten (oder bemerkenswerten Produkten). Sie können sehen, wie die Formeln aller bemerkenswerten Identitäten lauten, sowie Beispiele und Übungen, die Schritt für Schritt gelöst werden. Außerdem zeigen wir Ihnen, wozu diese berühmten mathematischen Regeln dienen.

👉👉 Im Folgenden erklären wir Schritt für Schritt jede bemerkenswerte Identität. Wenn Sie möchten, können Sie jedoch direkt zur Tabelle gehen 😉, in der alle Formeln zusammengefasst sind . 👈👈

Was sind bemerkenswerte Identitäten (oder bemerkenswerte Produkte)?

Bemerkenswerte Identitäten , auch bemerkenswerte Produkte oder bemerkenswerte Gleichungen genannt, sind mathematische Regeln, die es ermöglichen, Operationen mit Polynomen direkt zu lösen.

Die gebräuchlichsten Identitätsformeln sind das Quadrat einer Summe , das Quadrat einer Differenz (oder Subtraktion) und die Summe mal der Differenz .

bemerkenswerte Produktidentitäten oder -gleichheiten

Im Folgenden zeigen wir Ihnen jedoch nicht nur, wie Sie diese bemerkenswerten Produkte berechnen, sondern zeigen Ihnen auch alle Arten bemerkenswerter Identitäten, die es gibt.

Bemerkenswerte Identitätsformeln (oder Produkte)

Sobald wir die Definition bemerkenswerter Produkte (oder bemerkenswerter Gleichheiten) gesehen haben, werden wir sehen, wie die Formeln für bemerkenswerte Identitäten lauten. Wenn Sie andererseits an Formeldemos interessiert sind, können Sie diese ansehen, indem Sie auf die Schaltflächen „Demo anzeigen“ klicken.

Quadrat einer Summe

Das Quadrat einer Summe oder Summe im Quadrat ist eine der wichtigsten bemerkenswerten Identitäten. Genauer gesagt handelt es sich um ein Binomial mit zwei positiven Termen hoch 2, das heißt, sein algebraischer Ausdruck ist (a+b) ² .

Die Formel für das Quadrat einer Summe lautet also:

bemerkenswerte Identitäten im Quadrat mit einer Summe

Sehen Sie sich die Formeldemonstration an

Wenn wir von einem auf 2 angehobenen positiven Binomial ausgehen:

$(a+b)^2$

Mathematisch entspricht das obige Quadrat dem Faktor

$(a+b)$

mit sich selbst multipliziert:

$(a+b)^2=(a+b)\cdot (a+b)$

Wir multiplizieren also Polynome mit der Verteilungseigenschaft:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Von den vier erhaltenen Begriffen

$ab$

Und

$ba$

sehen ähnlich aus, damit wir sie gruppieren können:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

So sehr, dass wir bereits beim Ausdruck der Formel für eine quadrierte Summe angelangt sind, aus der sie abgeleitet wird:

$(a+b)^2= a^2+2ab+b^2$

Kurioserweise wird die Entwicklung des Ausdrucks für diese Art bemerkenswerter Produkte als perfektes quadratisches Trinom bezeichnet.

Damit ist das Quadrat einer Summe gleich dem Quadrat des ersten Termes plus dem doppelten Produkt des ersten mit dem zweiten plus dem Quadrat des zweiten.

Um eine quadrierte Summe zu lösen, reicht es also nicht aus, jede Addition auf beide zu erhöhen, sondern zusätzlich müssen die beiden Additionen miteinander und mit 2 multipliziert werden. Dies ist wichtig, sich daran zu erinnern, da es sich um einen sehr typischen Fehler dieser Art handelt des Produkts Es ist bemerkenswert, diesen Begriff zu vergessen.

bemerkenswerte polynomische und binomiale Identitäten

Beispiel:

Berechnen Sie die folgende bemerkenswerte Identität, indem Sie die entsprechende Formel anwenden:

$(x+5)^2$

Wie wir gerade gesehen haben, lautet die Formel für die bemerkenswerte Gleichheit einer quadrierten Summe:

$(a+b)^2=a^2+2ab+b^2$

Daher müssen wir zunächst die Parameter identifizieren

$a$

Und

$b$

der Formel. In diesem Fall,

$a$

repräsentiert die

$x$

des Paares und

$b$

entsprechen Nummer 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Nun, da wir die Werte kennen

$a$

und von

$b,$

Wir können die Formel für ein quadriertes positives Binomial verwenden, um das Ergebnis zu ermitteln:

Beispiele für bemerkenswerte quadratische Identitäten

Quadrat einer Differenz

Das Quadrat einer Differenz oder das Quadrat der Differenz ist eine weitere der drei am häufigsten verwendeten bemerkenswerten Identitäten. Insbesondere entspricht es einem Binomial, das aus einem positiven Term und einem anderen negativen Term, der auf 2 erhöht wird, gebildet wird, das heißt, dass sein algebraischer Ausdruck (ab) ² ist.

Die Formel für das Quadrat einer Differenz (oder das Quadrat einer Subtraktion) lautet also wie folgt:

Sehen Sie sich die Formeldemo an

Aus dem Binomialausdruck einer quadrierten Subtraktion:

$(a-b)^2$

Offensichtlich ist die vorherige Potenz gleich dem Produkt des Faktors

$(a-b)$

mit sich selbst multipliziert:

$(a-b)^2= (a-b)\cdot (a-b)$

Jetzt multiplizieren wir die beiden Klammern, indem wir die Verteilungseigenschaft anwenden:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

Sie müssen also nur noch ähnliche Begriffe gruppieren, um die Formel zu überprüfen:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Dann wird die Formel für das Quadrat einer Differenz mathematisch bewiesen:

$(a-b)^2=a^2-2ab+b^2$

Das Quadrat einer Differenz ist also gleich dem Quadrat des ersten Termes, minus dem doppelten Produkt des ersten mit dem zweiten, plus dem Quadrat des zweiten.

Was die bemerkenswerte Gleichheit des Summenquadrats angeht, dürfen wir nicht vergessen, den Mittelterm der Formel anzugeben, da die folgende Gleichung falsch ist:

Beispiel:

Lösen Sie die folgende bemerkenswerte Gleichheit einer quadrierten Differenz:

$(x-3)^2$

Da es sich um das bemerkenswerte Produkt einer quadrierten Subtraktion handelt, muss die entsprechende Formel angewendet werden:

$(a-b)^2=a^2-2ab+b^2$

Als nächstes müssen wir die Werte der Unbekannten ermitteln.

$a$

Und

$b$

der Formel. In diesem Fall,

$a$

ist die Variable

$x$

Und

$b$

entsprechen Nummer 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Beachten Sie, dass das negative Vorzeichen nicht Teil des Parameters ist

$b,$

Sie müssen jedoch immer die Zahl ohne Vorzeichen nehmen, um diese Formel korrekt anzuwenden.

Wir kennen daher bereits die Werte von

$a$

und von

$b$

Daher reicht es aus, diese Werte in die Formel einzusetzen, um die bemerkenswerte Identität aufzulösen:

Beispiele und Übungen, die Schritt für Schritt zu bemerkenswerten Gleichheiten gelöst werden

Summe durch Differenz

Das Produkt einer Summe und einer Differenz ist eine der drei am häufigsten verwendeten bemerkenswerten Identitäten. Wie der Name schon sagt, handelt es sich um ein positives Binomial, multipliziert mit seinem konjugierten Binomial (dasselbe Binomial, aber mit geändertem Zwischenzeichen). Das heißt, der algebraische Ausdruck dieses bemerkenswerten Produkts ist (a +b) · (ab). .

Die Formel für die bemerkenswerte Identität des Produkts einer Summe mit einer Differenz lautet wie folgt:

Identitäten, Produkte und bemerkenswerte Gleichheiten der High Schools 2, 3 und 4, die

Sehen Sie sich die Formeldemonstration an

Ausgehend vom Produkt einer Summe durch eine Subtraktion zweier beliebiger Terme:

$(a+b)\cdot (a-b)$

Um die Formel zu demonstrieren, müssen wir lediglich die erste Klammer mit der zweiten Klammer multiplizieren und dabei die Verteilungseigenschaft verwenden:

$\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}$

Jetzt gruppieren wir ähnliche Begriffe:

$a^2 -ab+ba-b^2=a^2-b^2$

Und wir haben damit den Ausdruck bemerkenswerter Gleichheit erreicht. Damit wird die Formel für diesen bemerkenswerten Identitätstyp demonstriert:

$(a+b)\cdot (a-b) =a^2-b^2$

Somit ist das Produkt der Summe und der Differenz zweier Größen gleich der Differenz der Quadrate dieser Größen. Oder mit anderen Worten: Das Multiplizieren der Summe zweier verschiedener Terme durch Subtrahieren derselben beiden Terme ist gleichbedeutend damit, jeden der beiden Terme zu quadrieren und zu subtrahieren.

Beispiel:

Finden Sie mit der entsprechenden Formel das folgende bemerkenswerte Produkt der Summe durch die Differenz zweier verschiedener Terme:

$(x+2)\cdot (x-2)$

Wie wir oben gesehen haben, lautet die Formel für die bemerkenswerte Gleichheit einer Summe multipliziert mit einer Differenz wie folgt:

$(a+b)\cdot (a-b) =a^2-b^2$

Zunächst müssen wir die Werte der Buchstaben ermitteln

$a$

Und

$b$

der Formel. In diesem Fall

$a$

entsprechen der Variablen

$x$

Und

$b$

entsprechen Nummer 2.

$\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

Und wenn wir bereits wissen, welche Werte die Parameter annehmen

$a$

Und

$b,$

Wir wenden die Formel für das Produkt der Summe mit der Differenz an:

Quadrat eines Trinoms

Das Quadrat eines Trinoms (aus drei Termen gebildetes Polynom) ist gleich dem Quadrat des ersten Termes, plus dem Quadrat des zweiten Termes, plus dem Quadrat des dritten Termes, plus dem Doppelten des ersten durch den zweiten, plus dem Doppelten des ersten für den dritten, plus das Doppelte des zweiten für den dritten.

Wie lauten die Formeln für alle bemerkenswerten Identitäten, Produkte oder Gleichheiten?

Sehen Sie sich die Formeldemo an

Aus einem beliebigen Trinomquadrat:

$(a+b+c)^2$

Das obige Quadrat kann mit sich selbst multipliziert in das Trinom faktorisiert werden:

$(a+b+c)^2 = (a+b+c)(a+b+c)$

Jetzt lösen wir die Polynommultiplikation:

$(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2$

Und schließlich gruppieren wir ähnliche Begriffe:

$a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc$

Auf diese Weise sind wir bereits beim Ausdruck der Formel angelangt, sodass die Formel für das Quadrat eines Trinoms demonstriert wird:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Beispiel:

Finden Sie die folgende bemerkenswerte Gleichheit:

$\left(x^2+x+3\right)^2$

Die Formel für das Quadrat eines Trinoms lautet:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Wie bei allen bemerkenswerten Gleichungen müssen Sie zunächst die Werte der Unbekannten in der Formel ermitteln. In dieser Übung

$a$

Ost

$x^2,$

der Koeffizient

$b$

entsprechen dem

$x,$

Und

$c$

ist der unabhängige Term 3:

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}$

Und wenn wir die Werte bereits kennen, setzen Sie diese Werte einfach in die Formel ein und führen Sie die Berechnungen durch:

Rechner für bemerkenswerte Identitäten, Produkte und Gleichheiten

Bemerkenswerte Identitäten (oder Produkte) gewürfelt

Wir haben gerade alle bemerkenswerten Identitäten im Quadrat untersucht, das heißt alle Arten von bemerkenswerten Identitäten, die durch auf 2 erhöhte Potenzen gebildet werden. Nun werden wir bemerkenswerte Identitäten im Quadrat analysieren. Natürlich sind Würfelidentitätsformeln etwas komplizierter, aber sie sind auch sehr nützlich.

Würfel einer Summe

Das bemerkenswerte Kubikprodukt einer Summe ist ein Binomial (Polynom mit nur zwei Monomen) hoch 3, dessen zwei Elemente positiv sind. Daher wird die Potenz einer Summe algebraisch als (a+b) ³ ausgedrückt.

Die Formel für die bemerkenswerte Gleichheit der Potenz einer Summe lautet:

Was sind alles bemerkenswerte Produkte, Identitäten oder Bindungen?

Sehen Sie sich die Formeldemonstration an

Ausgehend von einem positiven Binomial in Kubikzahl:

$(a+b)^3$

Die obige Potenz kann in das Produkt des Faktors eingerechnet werden

$(a+b)$

durch sein Quadrat:

$(a+b)^3=(a+b)\cdot (a+b)^2$

Ebenso, wie wir bei bemerkenswerten quadratischen Gleichungen gesehen haben, das Binomial

$(a+b)$

Es kann mit der Formel für das Quadrat einer Summe gelöst werden:

$(a+b)\cdot (a+b)^2=(a+b)\cdot (a^2+2ab+b^2)$

Dann multiplizieren wir die beiden Polynome miteinander:

$\begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}$

Zum Schluss müssen wir nur noch ähnliche Begriffe zusammenfassen:

$a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 = a^3+3a^2b+3ab^2+b^3$

Und damit ist die Formel für die bemerkenswerte Identität eines kubierten Summenbinomials verifiziert:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Kurz gesagt, eine auf 3 erhöhte Summe ist gleich der dritten Potenz des ersten plus dem Dreifachen des Quadrats des ersten mal dem zweiten, plus dem dreifachen des ersten mal dem Quadrat des zweiten plus der dritten Potenz des zweiten.

Beispiel:

Lösen Sie die folgende bemerkenswerte Identität einer Kubiksumme mithilfe der entsprechenden Formel:

$(x+2)^3$

In diesem Problem haben wir ein Binomial hoch 3, dessen beide Terme positiv sind. Wir müssen daher die Formel für eine Kubiksumme verwenden:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Wir müssen nun den Wert der Parameter ermitteln

$a$

Und

$b$

der Formel. In diesem Fall,

$a$

entsprechen der Variablen

$x$

Und

$b$

ist Nummer 2.

$\left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

Womit wir das bemerkenswerte Produkt berechnen, indem wir die Werte von ersetzen

$a$

und von

$b$

in der Formel:

10 Beispiele für bemerkenswerte Produkte oder Identitäten

Würfel einer Differenz

Der Würfel einer Differenz oder der Würfel einer Subtraktion ist ein Binomial zur Potenz von 3, dessen Term ein negatives Vorzeichen hat. Der mathematische Ausdruck für diesen bemerkenswerten Produkttyp lautet also (ab) ³ .

Die Formel für den Würfel einer Differenz (oder Subtraktion) lautet:

bemerkenswerte kubische Identitäten, Produkte oder Gleichheiten

Sehen Sie sich die Formeldemonstration an

Offensichtlich ist der Beweis dieser Formel dem des bemerkenswerten Produkts einer kubierten Summe sehr ähnlich. Aber in diesem Fall gehen wir von einem negativen kubischen Binomial aus:

$(a-b)^3$

Offensichtlich kann die vorherige Potenzierung in das Produkt des Faktors zerlegt werden

$(a-b)$

multipliziert mit seinem Quadrat:

$(a-b)^3=(a-b)\cdot (a-b)^2$

Also, wie wir in bemerkenswerten quadratischen Identitäten untersucht haben, das Binomial

$(a-b)$

Es kann mit der Formel für das Quadrat einer Differenz berechnet werden:

$(a-b)\cdot (a-b)^2=(a-b)\cdot (a^2-2ab+b^2)$

Wir erzeugen nun das Produkt der beiden Polynome:

$\begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}$

Und der letzte Schritt besteht darin, ähnliche Begriffe zu gruppieren:

$a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 = a^3-3a^2b+3ab^2-b^3$

Damit ist die Formel für die bemerkenswerte Identität eines subtrahierten Binomials in der Kubikzahl verifiziert:

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

Eine auf drei erhöhte Differenz (oder Subtraktion) entspricht also der dritten Potenz des ersten, minus dem Dreifachen des Quadrats des ersten mal dem zweiten, plus dem Dreifachen des ersten mal dem Quadrat des zweiten, minus der dritten Potenz des zweiten.

Beispiel:

Berechnen Sie das nächste kubische Binomial (Differenz) mithilfe der entsprechenden Formel:

$(3x-2)^3$

In dieser Übung haben wir ein Paar mit einem positiven und einem negativen Element. Wir müssen daher die Formel für eine kubische Differenz verwenden:

$(a-b)^3 = a^3-3a^2b+3ab^2 -b^3$

Zuerst ermitteln wir wie immer den Wert der Unbekannten

$a$

Und

$b$

der Formel. In diesem Fall

$a$

stellt das Monom dar

$3x$

Und

$b$

ist der unabhängige Term des Binomials, also 2.

$\left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}$

Beachten Sie, dass der Parameter

$b$

ist einfach gleich 2, ohne das negative Vorzeichen der Zahl. Es ist wichtig, dies im Hinterkopf zu behalten, um die Formel richtig anzuwenden.

Schließlich finden wir die bemerkenswerte Identität, indem wir die Werte von setzen

$a$

und von

$b$

in der Formel:

entwickeln bemerkenswerte Identitäten, Produkte und Gleichheiten

Übersichtstabelle bemerkenswerter Identitäten

Zusammenfassend haben wir eine Tabelle mit allen bemerkenswerten Identitäten (oder Produkten) erstellt, die wir gesehen haben, damit Sie sie leichter studieren können. 😉

Formeln für Identitäten oder Gleichheiten bemerkenswerter Produkte

Gelöste Übungen zu bemerkenswerten Identitäten (oder Produkten)

Damit Sie den Begriff bemerkenswerter Identitäten, auch bemerkenswerte Produkte oder bemerkenswerte Gleichheiten genannt, vollständig verstehen, haben wir mehrere Übungen vorbereitet, die Schritt für Schritt gelöst werden. Sie können versuchen, sie zu machen und dann überprüfen, ob Sie mit den Lösungen der Übungen gut zurechtgekommen sind.

⬇⬇ Vergessen Sie nicht, dass Sie uns alle Ihre Fragen unten in den Kommentaren stellen können! ⬇⬇

Übung 1

Erweitern Sie die folgenden bemerkenswerten Identitäten (Summenquadrate):

$\text{A)} \ (x+3)^2$

$\text{B)} \ (6x+2)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

siehe Lösung

Alle bemerkenswerten Identitäten im Problem sind Quadratsummen, daher müssen wir in diesem Fall immer dieselbe Formel anwenden:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Übung 2

Entwickeln Sie die folgenden bemerkenswerten Produkte (Differenzen im Quadrat):

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

siehe Lösung

Alle nennenswerten Produkte in dieser Übung sind quadrierte Subtraktionen, daher müssen wir nur eine Formel anwenden:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

Übung 3

Entwickeln Sie die folgenden bemerkenswerten Gleichungen (Produkte von Summen und Differenzen):

$\text{A)} \ (x+5)(x-5)$

$\text{B)} \ (2x+6)(2x-6)$

$\text{C)} \ (x+7)(x-7)$

$\text{D)} \ (x-4y)(x+4y)$

siehe Lösung

Da alle wichtigen Gleichungen in dieser Übung Multiplikationen von Summen mit Differenzen sind, werden sie alle mit derselben Formel gelöst:

$(a+b)\cdot (a-b) =a^2-b^2$

$\text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}$

$\text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}$

$\text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}$

$\text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}$

Übung 4

Lösen Sie alle folgenden bemerkenswerten Identitäten auf:

$\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)$

$\text{B)} \ \left(4x^2+2y^3\right)^2$

$\text{C)} \ \left(6x^3-4y^4\right)^2$

$\text{D)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)$

$\text{E)} \ \left(5x^2-9x\right)^2$

siehe Lösung

$\text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

$\text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}$

$\text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}$

Übung 5

Berechnen Sie die folgenden bemerkenswerten Produkte:

$\text{A)} \ (x+4)^3$

$\text{B)} \ \left(x^2-5\right)^3$

$\text{C)} \ \left(2x-1\right)^3$

$\text{D)} \ (5x+2)^3$

siehe Lösung

Um alle nennenswerten Produkte des Problems zu finden, ist es notwendig, die Formeln für eine Summe und eine entsprechend den Fällen kubierte Differenz anzuwenden:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

$\text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}$

Übung 6

Lösen Sie die folgenden bemerkenswerten Gleichungen:

$\text{A)} \ \left(x^2+x+5\right)^2$

$\text{B)} \ \left(x^2+3x-4\right)^2$

$\text{C)} \ \left(4x^2-6x+3\right)^2$

$\text{D)} \ \left(x^3-3x^2-9x\right)^2$

siehe Lösung

Um alle diese bemerkenswerten Identitäten zu lösen, müssen wir die Formel für das Quadrat eines Trinoms verwenden, die lautet:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

$\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}$

$\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}$

$\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}$

$\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}$

Übung 7

Berechnen Sie die folgenden bemerkenswerten Identitäten mit Wurzeln und Brüchen (hoher Schwierigkeitsgrad):

$\text{A)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

$\text{D)} \ \Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr)$

siehe Lösung

Abschnitt A) besteht aus einer quadrierten Subtraktion. Um sie zu lösen, muss die entsprechende Formel angewendet werden. Außerdem muss beachtet werden, dass eine quadrierte Wurzel vereinfacht wird:

$\text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

Abschnitt B) befasst sich mit der Addition durch Subtraktion und Monome haben Bruchkoeffizienten, mit denen dieses bemerkenswerte Produkt mithilfe der Formel für Addition durch Subtraktion und den Eigenschaften von Brüchen bestimmt werden muss:

$\text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}$

Die bemerkenswerte Gleichheit in Abschnitt C) ist eine auf 2 erhöhte Summe und besteht ebenfalls aus Brüchen. Um es zu berechnen, müssen wir daher die Formel für eine quadrierte Summe plus die Eigenschaften von Brüchen verwenden:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

Die letzte bemerkenswerte Identität befasst sich mit einer Summe mal einer Differenz mit irrationalen Koeffizienten, daher wenden wir die Formel für eine Summe mal einer Differenz an und vereinfachen dann die Quadratwurzeln:

$\text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}$

Andere bemerkenswerte Identitätstypen

Alle oben besprochenen bemerkenswerten Identitäten werden am häufigsten verwendet. Allerdings gibt es in der Mathematik auch andere bemerkenswerte Produkttypen, die interessant zu kennen sind, da sie für unterschiedliche Zwecke verwendet werden.

Summe der Würfel

Die Summe der Kubikzahlen entspricht einem Binomial, dessen beide Terme positiv sind und dessen Kubikwurzeln außerdem exakt sind. Daher ist der algebraische Ausdruck für eine Würfelsumme a ³ +b ³ .

Bemerkenswerte Identitäten, Produkte oder Verbindungen geklärt

Die Formel für dieses bemerkenswerte Produkt wird verwendet, um ein Polynom zu faktorisieren, das heißt, durch die Formel transformieren wir ein Polynom in ein Produkt eines Binomials durch ein Trinom.

Damit Sie sehen können, wie es gemacht wird, finden Sie hier eine Beispielanwendung dieser bemerkenswerten Identität:

$x^3+8$

Tatsächlich besteht der vorherige Ausdruck aus einer Addition von Kubikzahlen, da die Kubikwurzel des Monoms ist

$x^3$

ist genau (gibt keine Dezimalzahl an) und die Zahl 8 auch:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{8} = 2$

$x^3+8=x^3+2^3$

Daher können wir die Formel für die Summe perfekter Würfel verwenden, um den kubischen Ausdruck in ein Produkt aus einem Binomial und einem Trinom umzuwandeln:

$a^3+b^3 = (a+b)(a^2-ab+b^2)$

$\begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}$

Differenz der Würfel

Die Differenz (oder Subtraktion) von Würfeln ist ein Binomial, das aus einem positiven Term und einem negativen Term besteht, deren kubische Wurzeln exakt sind. Mit anderen Worten, eine Würfeldifferenz wird in der Form a ³ -b ³ ausgedrückt.

Gelöste Übungen zur Faktorisierung von Polynomen mit bemerkenswerten Identitäten

Machen wir ein Beispiel, damit Sie sehen können, wie dieser bemerkenswerte Identitätstyp aufgelöst wird:

$x^3-27$

Es handelt sich um eine Differenz von Kubikzahlen, da beide die Kubikwurzel des Monoms sind

$x^3$

da 27 richtig sind:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{27} = 3$

$x^3-27=x^3-3^3$

Sie können daher die Formel für die Differenz perfekter Würfel verwenden, um das Binomial zu faktorisieren:

$a^3-b^3 = (a-b)(a^2+ab+b^2)$

$\begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}$

Produkt von Binomialen mit einem gemeinsamen Begriff

Dieses bemerkenswerte Produkt wird verwendet, um ein Produkt zweier Binome, die einen gemeinsamen Term haben, in ein quadratisches Polynom umzuwandeln.

bemerkenswerte Identitäten, Produkte oder Gleichheiten pdf

Hier ist ein ausführliches Beispiel für ein bemerkenswertes Produkt dieser Art:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

mehr Identitäten

Obwohl bemerkenswerte Identitäten am bekanntesten sind, weil sie am häufigsten vorkommen, sollte beachtet werden, dass es auch mehr Identitäten mit anderen Namen gibt. Hier ist eine Liste anderer weniger bekannter Identitäten, falls Sie neugierig sind:

Lagrange-Identitäten:

$(a^2+b^2)\cdot (x^2+y^2) =(ax+by)^2+(ay-bx)^2$
$(a^2-b^2)\cdot (x^2-y^2) =(ax+by)^2-(ay+bx)^2$

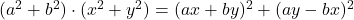
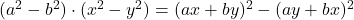
Legendre-Identitäten:

$(a+b)^2+(a-b)^2=2(a^2+b^2)$
$(a+b)^2-(a-b)^2=4ab$
$(a+b)^4-(a-b)^4=8ab(a^2+b^2)$

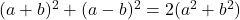
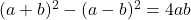
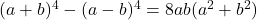
Argands Identität:

$(x^2+x+1)(x^2-x+1) = x^4+x^2+1$

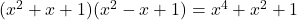
Gaußsche Identitäten:

$a^3+b^3+c^3-3abc= (a+b+c)(a^2+b^2+c^2-ab-bc-ac)$
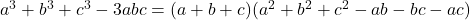
$a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]$

Bemerkenswerte Identitäts-Apps

Wenn Sie es bis hierher geschafft haben, bedeutet das, dass Sie bereits wissen, wie man Berechnungen mit bemerkenswerten Identitäten durchführt. Hell! Aber wirklich… wozu gibt es bemerkenswerte Identitäten? Und wann werden bemerkenswerte Identitäten verwendet?

Wie wir in diesem Artikel gesehen haben, besteht der Hauptzweck bemerkenswerter Identitäten darin, Berechnungen zu vereinfachen. Das heißt, dass wir dank bemerkenswerter Produkte bestimmte Potenzen komplexer Polynome direkt lösen können, ohne schwierige Operationen durchführen zu müssen.

Aber bemerkenswerte Gleichheiten haben auch andere Funktionen, wie zum Beispiel das Faktorisieren von Polynomen und das Ergänzen von Quadraten. Dann werden wir sehen, woraus jede dieser Anwendungen besteht.

Faktorisierung von Polynomen

Einige sehr spezifische Arten von Polynomen können mit bemerkenswerten Identitäten faktorisiert werden. Wenn wir beispielsweise ein Polynom finden, das aus zwei Termen besteht, die perfekte Quadrate sind (ihre Quadratwurzeln sind exakt), können wir es mithilfe der bemerkenswerten Gleichheitsformel des Produkts einer Summe mit einer Differenz faktorisieren:

$a^2-b^2 =(a+b)(a-b)$

$x^2-9 =(x+3)(x-3)$

Ebenso können Trinome, die die bemerkenswerte Identität des Quadrats einer Addition oder Subtraktion berücksichtigen, faktorisiert werden:

$a^2+2ab+b^2=(a+b)^2$

$x^2+4x+4=(x+2)^2$

$a^2-2ab+b^2=(a-b)^2$

$x^2-10x+25=(x-5)^2$

Ebenso können, sobald ein Polynom faktorisiert wurde, die Wurzeln (oder Nullstellen) dieses Polynoms gefunden werden. Allerdings ist dieses Konzept etwas komplizierter zu verstehen. Wenn Sie also mehr Interesse haben, empfehlen wir Ihnen, die Erklärung in der Suchmaschine auf unserer Website (oben rechts) zu suchen, da wir einen ganzen Artikel haben, der es erklärt.

quadratischer Abschluss

Das Vervollständigen von Quadraten ist ein mathematisches Verfahren, mit dem ein quadratisches Trinom in die Summe eines Quadrats plus (oder minus) einer Zahl umgewandelt wird.

Gegeben sei ein Trinom:

$ax^2+bx+c$

Dann lässt sich das Trinom in den folgenden Ausdruck umwandeln:

$a(x+h)^2+k$

wo die Parameter

$h$

Und

$k$

werden mit folgenden Formeln berechnet:

$h=\cfrac{b}{2a} \qquad \qquad k=c-ah^2$

Auch wenn es Ihnen nicht so vorkommt, sind diese beiden Formeln auf bemerkenswerte Identitäten zurückzuführen. Dank der bemerkenswerten Produkte können die Quadrate vervollständigt werden.

Als Beispiel wenden wir dieses Verfahren auf das folgende Trinom an:

$2x^2+4x+3$

Wir berechnen die Parameter

$h$

Und

$k:$

$h=\cfrac{b}{2a}=\cfrac{4}{2\cdot 2} =1$

$k=c-ah^2 = 3-2\cdot 1^2 = 1$

Und deshalb bleibt das Polynom:

$2(x+1)^2+1$

Bemerkenswerte identitäten (oder bemerkenswerte produkte)

Was sind bemerkenswerte Identitäten (oder bemerkenswerte Produkte)?

Bemerkenswerte Identitätsformeln (oder Produkte)

Quadrat einer Summe

Beispiel:

Quadrat einer Differenz

Beispiel:

Summe durch Differenz

Beispiel:

Quadrat eines Trinoms

Beispiel:

Bemerkenswerte Identitäten (oder Produkte) gewürfelt

Würfel einer Summe

Beispiel:

Würfel einer Differenz

Beispiel:

Übersichtstabelle bemerkenswerter Identitäten

Gelöste Übungen zu bemerkenswerten Identitäten (oder Produkten)

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Übung 6

Übung 7

Andere bemerkenswerte Identitätstypen

Summe der Würfel

Differenz der Würfel

Produkt von Binomialen mit einem gemeinsamen Begriff

mehr Identitäten

Bemerkenswerte Identitäts-Apps

Faktorisierung von Polynomen

quadratischer Abschluss

Kommentar verfassen Kommentieren abbrechen