Auf dieser Seite sehen Sie, was die Ableitung des hyperbolischen Arkuskosinus (Formel) ist. Außerdem finden Sie Schritt für Schritt gelöste Übungen zu Ableitungen des hyperbolischen Arkuskosinus einer Funktion. Und schließlich finden Sie die Demonstration der Formel für die Ableitung dieser Art trigonometrischer Funktion.
Formel für die Ableitung des hyperbolischen Arcuscosinus
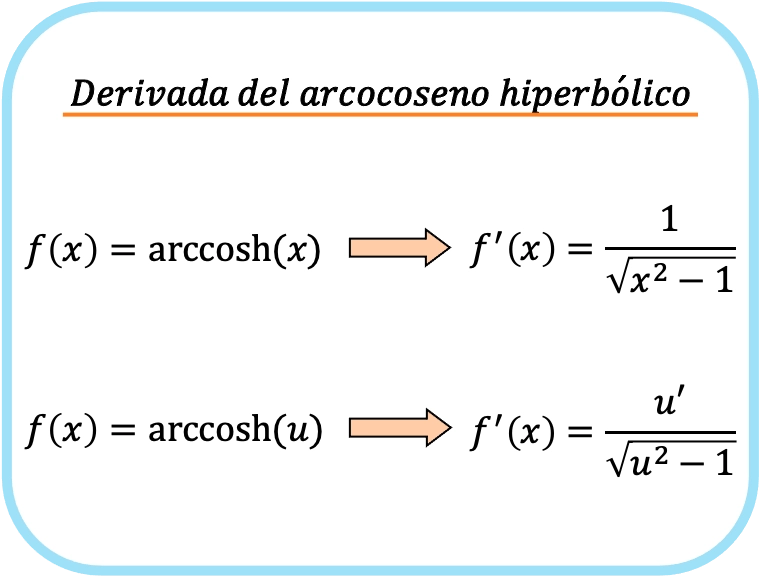
Die Ableitung des hyperbolischen Arkuskosinus von x ist eins über die Quadratwurzel von x im Quadrat minus 1.
![]()
Daher ist die Ableitung des hyperbolischen Arkuskosinus einer Funktion gleich dem Quotienten aus der Ableitung dieser Funktion geteilt durch die Quadratwurzel dieser Funktion im Quadrat minus eins.
![]()
Die zweite Formel beinhaltet die Kettenregel und kann daher zur Ableitung jedes hyperbolischen Arkuskosinus verwendet werden. Wenn wir x durch u ersetzen, erhalten wir tatsächlich die erste Formel. Stattdessen funktioniert die erste Formel nur für die hyperbolische Arkuskosinus-Ableitung von x.
Der hyperbolische Arkuskosinus ist die Umkehrfunktion des hyperbolischen Kosinus und daher hängen die beiden Funktionen zusammen. Sie können die Formel für die Ableitung dieser trigonometrischen Funktion sehen, indem Sie hier klicken:
➤ Siehe: Formel für die Ableitung des hyperbolischen Kosinus
Beispiele für die hyperbolische Arkussinus-Ableitung
Beispiel 1
![]()
Um die Ableitung des hyperbolischen Arkuskosinus zu finden, müssen wir die entsprechende Formel verwenden:
![]()
Deshalb müssen wir im Zähler des Bruchs die Ableitung von 5x einsetzen, also 5. Und im Nenner müssen wir nur die Quadratwurzel der Argumentfunktion zum Quadrat minus 1 einsetzen:
![]()
Beispiel 2
![]()
Die aus dieser Übung abzuleitende Funktion ist ein hyperbolischer Arkuskosinus, daher verwenden wir die folgende Formel, um sie abzuleiten:
![]()
Im Zähler schreiben wir also die Ableitung des Arguments der Funktion und im Nenner die Quadratwurzel der Funktion des Arguments erhöht auf 2 minus 1:
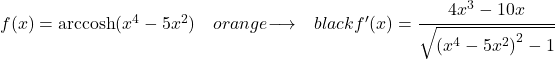
Beweis der Ableitung des hyperbolischen Arcuscosinus
Abschließend demonstrieren wir die Formel für die Ableitung des hyperbolischen Arcuscosinus.
![]()
Zuerst transformieren wir den hyperbolischen Arcuskosinus in einen hyperbolischen Kosinus:
![]()
Wir folgern aus beiden Seiten der Gleichheit:
![]()
Wir klären Sie:
![]()
Wir verwenden nun die trigonometrische Identität, die den hyperbolischen Sinus und den hyperbolischen Kosinus in Beziehung setzt, um den Nenner zu modifizieren:
![]()
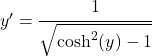
Allerdings haben wir zunächst gefolgert, dass x dem hyperbolischen Kosinus von y entspricht, sodass die Gleichung erhalten bleibt:
![]()