Übertreibung: Definition, Formel, Elemente, Gleichung, Beispiele, ...

Hier finden Sie alles über die Hyperbel: Was sie ist, was ihre charakteristischen Elemente sind, wie man ihre Gleichung findet, Beispiele, gelöste Aufgaben usw.

Was ist eine Übertreibung?

Die Hyperbel ist eine offene Kurve mit zwei Ästen, deren mathematische Definition wie folgt lautet:

In der analytischen Geometrie ist eine Hyperbel der Ort von Punkten auf der Ebene, der die folgende Bedingung erfüllt: Der Absolutwert der Abstandsdifferenz zwischen einem beliebigen Punkt der Hyperbel und zwei festen Punkten (Brennpunkten genannt) muss konstant sein.

Darüber hinaus entspricht der Wert der Subtraktion dieser beiden Abstände immer dem Abstand zwischen den beiden Eckpunkten der Hyperbel.

$\lvert d_1 - d_2 \rvert = 2a$

Unten sehen wir, was der Koeffizient bedeutet

$a$

einer Übertreibung.

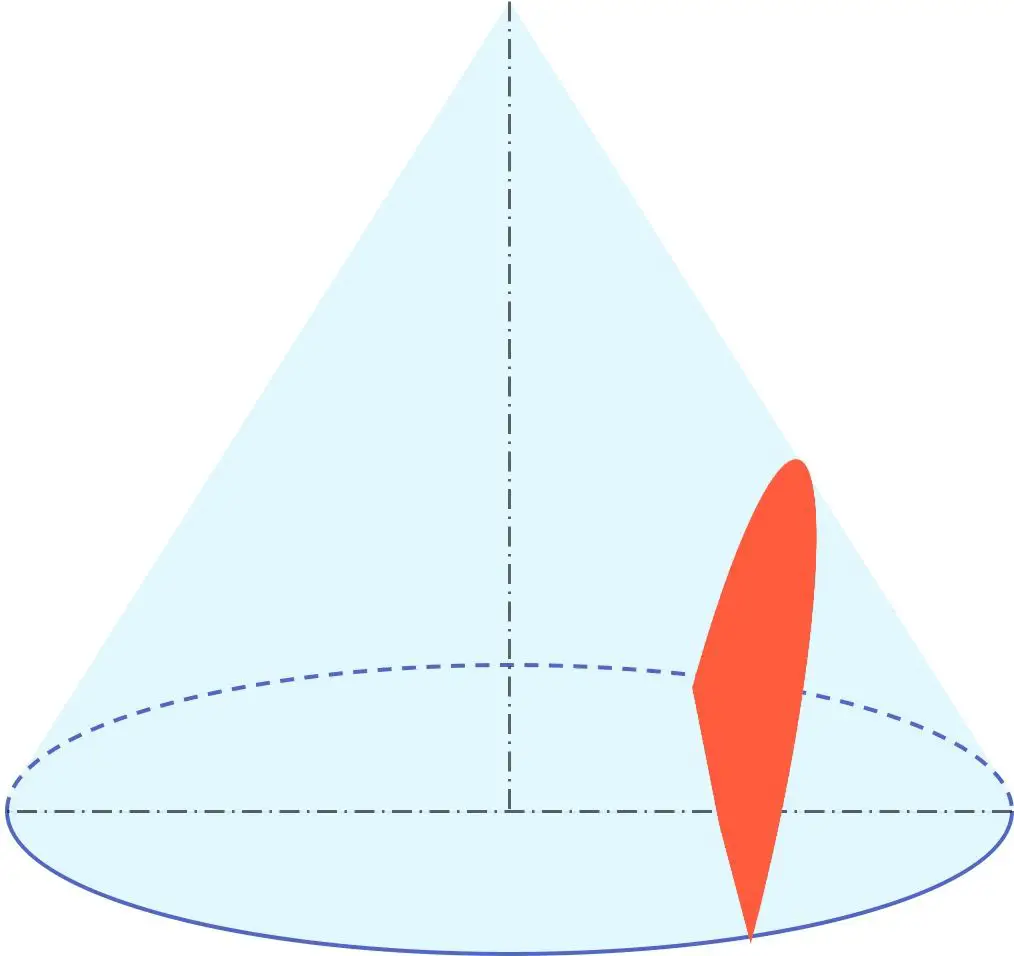
Darüber hinaus gehört die Hyperbel zusammen mit dem Umfang, der Ellipse und der Parabel zur geometrischen Gruppe, die Kegelschnitte genannt wird. Daher ist eine Hyperbel ein Kegelschnitt, oder mit anderen Worten, sie kann aus einem Kegel erhalten werden.

Insbesondere ist eine Hyperbel das Ergebnis des Schnitts eines Kegels durch eine Ebene mit einem Winkel, der kleiner ist als der Winkel, den der Erzeuger des Kegels mit seiner Rotationsachse bildet.

Elemente einer Hyperbel

Die Eigenschaften einer Hyperbel hängen von Folgendem ab:

Die Brennpunkte : Dies sind zwei für jede Hyperbel charakteristische Fixpunkte (Punkte F und F‘ in der Grafik unten). Der Absolutwert der Differenz zwischen den Abständen von jedem Punkt der Hyperbel zu jedem Fokus ist konstant und gleich
$2a.$
Brenn- oder Hauptachse : Dies ist die Linie, die durch die beiden Brennpunkte der Hyperbel verläuft. Sie entspricht einer Symmetrieachse dieser geometrischen Figur. Auch Quer- oder Querachse genannt.
Sekundärachse : Sie ist die Winkelhalbierende des Segments FF‘ (Linie, die durch die Punkte B und B‘ verläuft). Darüber hinaus ist es eine Linie senkrecht zur Brennachse und eine weitere Symmetrieachse der Hyperbel
Mittelpunkt (O) : ist der Schnittpunkt der beiden Achsen und der Mittelpunkt der beiden Scheitelpunkte und der beiden Brennpunkte. Da die Hyperbel zwei Symmetrieachsen hat, ist sie auch das Symmetriezentrum.
Eckpunkte (A und A‘) : sind die Schnittpunkte der Zweige der Hyperbel mit der Brennachse.
Vektorstrahlen (R) : Dies sind die Segmente, die von jedem Punkt der Hyperbel zu jedem Fokus verlaufen.
Brennweite : Dies ist die Länge des zusammengesetzten Segments zwischen den beiden Brennpunkten.
Hauptachse oder reale Achse: Dies ist das Segment, das von Punkt A zu Punkt A‘ verläuft und dessen Länge entspricht
$2a.$
Kleine Achse oder imaginäre Achse: Dies ist das Segment, das von Punkt B zu Punkt B‘ verläuft und dessen Länge entspricht
$2b.$
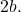
Asymptoten : sind die gepunkteten Linien, die im Diagramm angezeigt werden. Wir werden unten sehen, wie sie berechnet werden.

Beziehung zwischen den Elementen einer Hyperbel

Zunächst einmal sagen wir, dass Halbachse die Hälfte einer Achse bedeutet. Beispielsweise ist die wahre Halbachse das Segment, das vom Punkt A zum Mittelpunkt der Hyperbel verläuft und dessen Länge beträgt

$a.$

Somit besteht ein sehr wichtiger Zusammenhang zwischen der realen Halbachse, der imaginären Halbachse und der halben Brennweite. Tatsächlich wird die Formel, die wir als nächstes ableiten werden, häufig zur Lösung von Hyperbelübungen und -problemen verwendet.

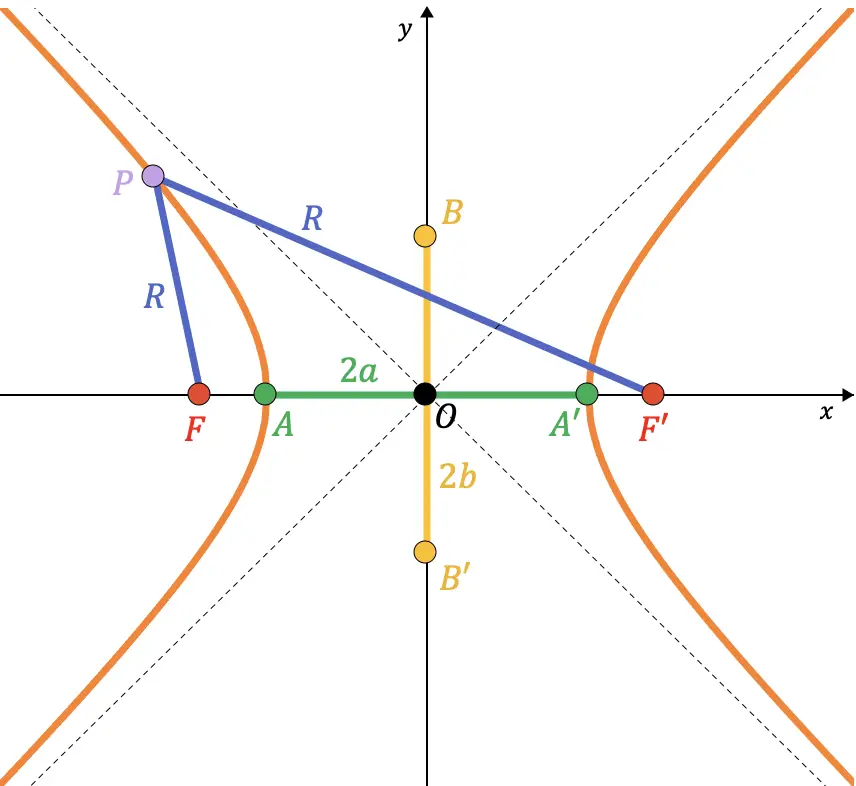
Sie sollten wissen, dass die Punkte B und B‘ einer Hyperbel den Schnittpunkten der Hauptachse und des imaginären Kreises mit Radius entsprechen

$c$

(Halbbrennweite) vom Mittelpunkt zum Punkt A. Wie Sie in der folgenden grafischen Darstellung sehen können, stimmt das Segment, das Punkt A und Punkt B verbindet, mit dem Radius des Kreises überein (

$c$

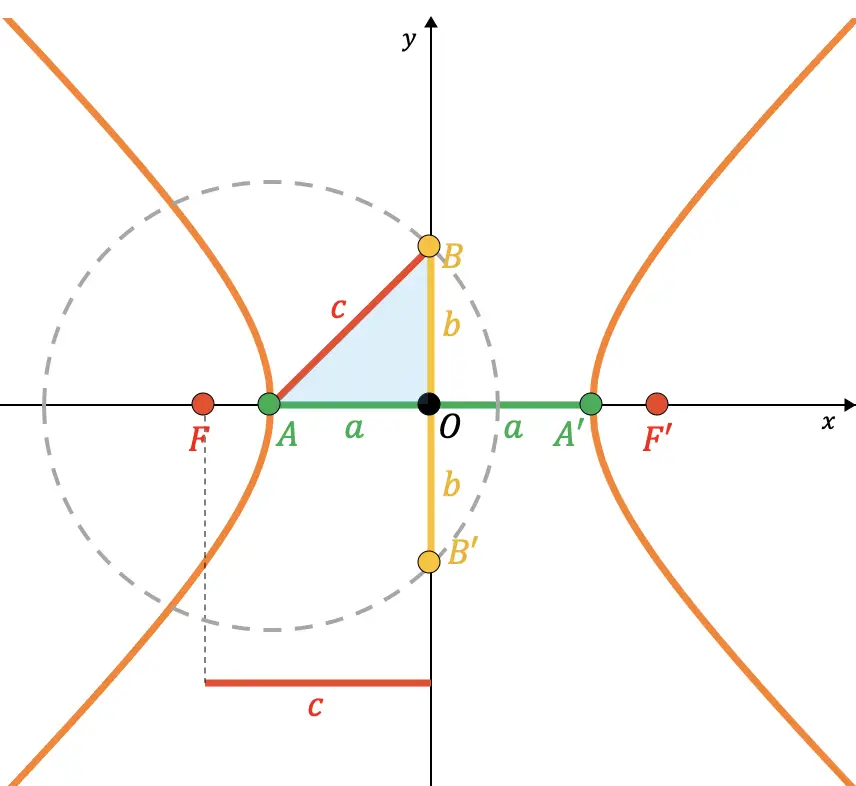
Beziehung zwischen den Elementen einer Hyperbel

Aus dem Satz des Pythagoras kann also gezeigt werden, dass die Beziehung zwischen den Parametern besteht

$a, b$

Und

$c$

ist das Folgende:

$c^2 = a^2+b^2$

Hyperbelgleichung

Es gibt verschiedene Arten von Hyperbelgleichungen, da je nach ihren Eigenschaften die eine oder die andere verwendet wird, um sie mathematisch auszudrücken. Als nächstes werden wir jeden im Detail analysieren.

Zuerst haben wir die gewöhnliche Gleichung der Hyperbel. Zweitens werden wir eine Variante der gewöhnlichen Gleichung sehen, das ist die reduzierte oder kanonische Gleichung der Hyperbel. Als nächstes werden wir untersuchen, wie die allgemeine Gleichung einer Hyperbel lautet. Und schließlich analysieren wir die Gleichungen zweier Spezialfälle von Hyperbeln: der gleichseitigen Hyperbel und der konjugierten Hyperbeln .

Gewöhnliche Gleichung der Hyperbel

Wenn wir durch eine Gleichung eine Hyperbel mit einem äußeren Mittelpunkt im Koordinatenursprung (Punkt (0,0)) definieren wollen, müssen wir die folgende Formel verwenden:

Die Formel für die gewöhnliche Gleichung der Hyperbel in kartesischen Koordinaten lautet wie folgt:

$\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1$

Gold:

$x_0$

Und

$y_0$

sind die Koordinaten des Mittelpunkts der Hyperbel:

$O(x_0,y_0)$
$a$

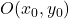
ist die Länge der großen Halbachse der Hyperbel.
$b$

ist die Länge der kleinen Halbachse der Hyperbel.

Mit dieser Gleichung kann man Hyperbeln beschreiben, deren Brennachse horizontal liegt (nach links und rechts offene Äste), was Hyperbeln normalerweise sind. Wenn wir jedoch mit einer vertikalen Brennachse arbeiten (Äste öffnen sich von oben nach unten), geht das negative Vorzeichen von der Variablen y auf die Variable x über:

$\cfrac{(y-y_0)^2}{a^2}-\cfrac{(x-x_0)^2}{b^2} = 1$

Gold

$x_0$

Und

$y_0$

sind wie zuvor die Koordinaten des Mittelpunkts der Hyperbel und die Terme

$a$

Und

$b$

Sie sind immer noch die große Halbachse und die kleine Halbachse der Hyperbel, obwohl diese beiden nun im Gegensatz zu zuvor vertikal bzw. horizontal ausgerichtet sind.

Kanonische oder reduzierte Gleichung der Hyperbel

Diese Art von Hyperbelgleichung ist der gewöhnlichen Gleichung sehr ähnlich. Der einzige Unterschied besteht darin, dass die kanonische Gleichung verwendet wird, um Hyperbeln analytisch auszudrücken, deren Mittelpunkt der Punkt (0,0) ist. Daher verwenden wir die kanonische oder reduzierte Gleichung der Hyperbel, wenn der Mittelpunkt der Hyperbel der Koordinatenursprung ist.

Wir werden nun die Formel für die reduzierte Gleichung der Hyperbel aus ihrer gewöhnlichen Gleichung ableiten:

$\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1$

Wenn der Mittelpunkt der Hyperbel der Koordinatenursprung, also der Punkt (0,0), sein soll, gilt immer:

$x_0 = 0$

$y_0 = 0$

Somit lautet die kanonische oder reduzierte Gleichungsformel der Hyperbel:

$\color{orange} \boxed{\color{black}\qquad\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1 \vphantom{\cfrac{\vphantom{\Bigl(}}{\vphantom{\Bigl(}}}\qquad }$

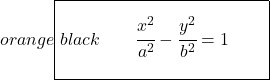
Wenn die Brennachse wie zuvor vertikal statt horizontal wäre, wäre die negative Variable x :

$\cfrac{y^2}{a^2}-\cfrac{x^2}{b^2} = 1$

Allgemeine Gleichung der Hyperbel

Die Formel für die allgemeine Gleichung einer Hyperbel lautet wie folgt:

$Ax^2 +Bxy+Cy^2 +Dx+Ey+F =0$

Damit die obige Gleichung jedoch eine Hyperbel ist, sind die Koeffizienten

$A$

Und

$C$

Sie müssen von Null verschieden sein und gleichzeitig das umgekehrte Vorzeichen haben.

Gleichseitige Hyperbelgleichung

Eine gleichseitige Hyperbel ist eine Hyperbel, bei der die Länge der realen Halbachse der Länge der imaginären Halbachse entspricht, das heißt

$a=b.$

Daher lautet die Gleichung einer gleichseitigen Hyperbel:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{a^2} = 1$

Außerdem stehen die Asymptoten der gleichseitigen Hyperbeln senkrecht zueinander. Und die Gleichungen dieser Linien lauten wie folgt:

$y=x$

$y=-x$

Wenn wir genau hinsehen, sind diese beiden Gleichungen die Winkelhalbierenden des ersten (und dritten) Quadranten bzw. des zweiten (und vierten) Quadranten. Wenn wir also eine gleichseitige Hyperbel um 45° nach links drehen, nehmen ihre Asymptoten die Stelle der Koordinatenachsen ein:

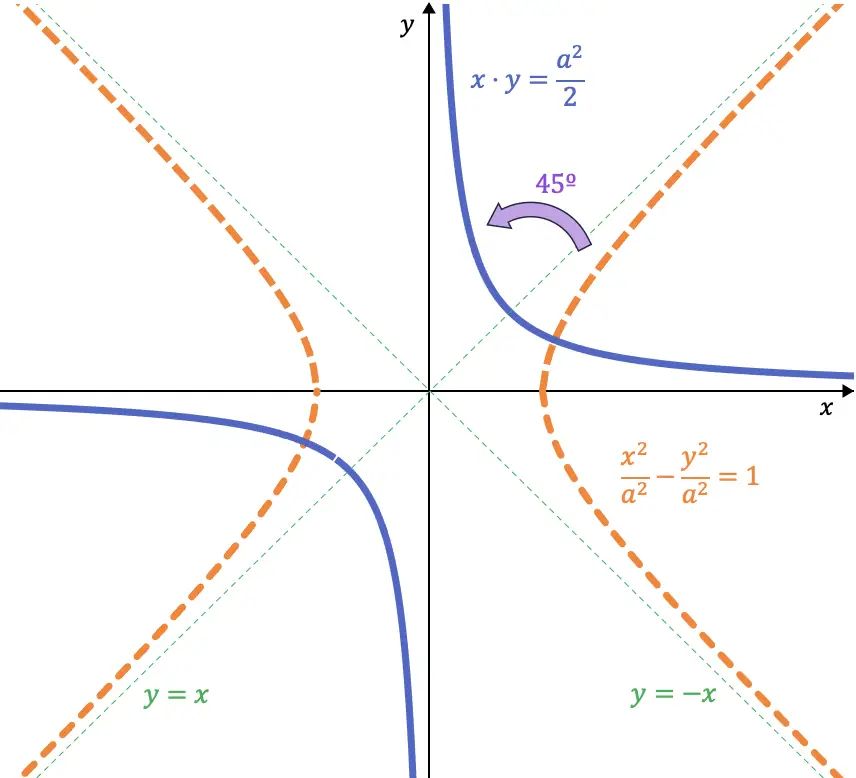
Wenn wir also die 45°-Kurve machen, lautet die Gleichung für die Hyperbel:

$x\cdot y = \cfrac{a^2}{k}$

konjugierte Hyperbeln

Zwei Hyperbeln sind konjugiert, wenn die reale Achse der einen mit der imaginären Achse der anderen übereinstimmt . Daher besteht der einzige Unterschied zwischen den Gleichungen zweier konjugierter Hyperbeln darin, welche Variable negiert wird, da die Koeffizienten der Nenner gleich bleiben müssen.

Hier ist ein Beispiel für die Gleichungen zweier miteinander konjugierter Hyperbeln:

$\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2}=1 \qquad \qquad \cfrac{y^2}{b^2}-\cfrac{x^2}{a^2} =1$

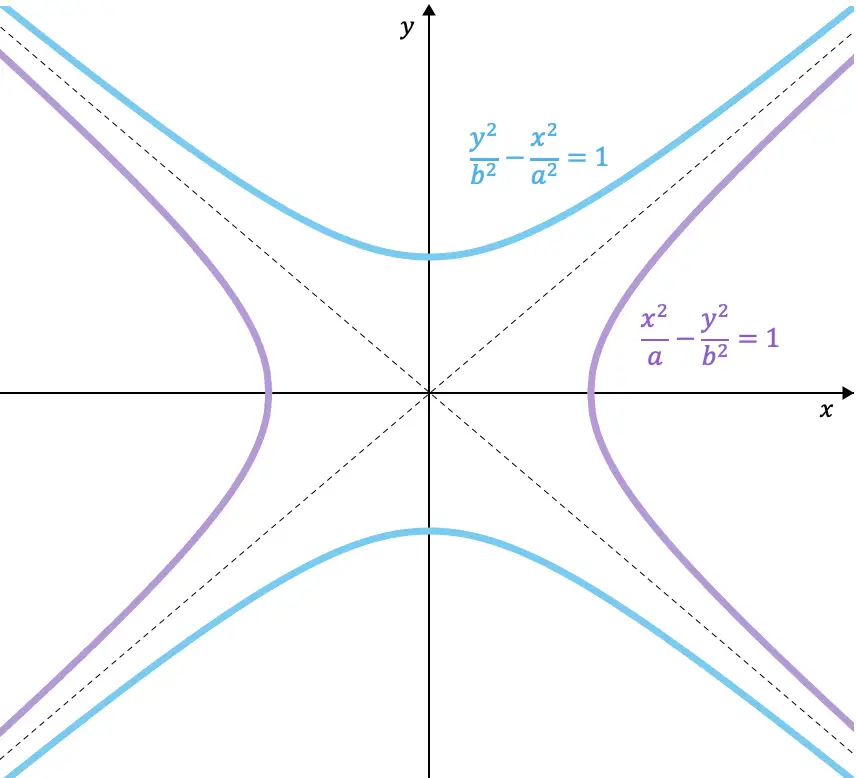
Darüber hinaus haben die konjugierten Hyperbeln, wie Sie an den grafisch dargestellten Hyperbeln erkennen können, die gleichen Asymptoten.

Asymptoten der Hyperbel

Wie Sie in den vorherigen Grafiken gesehen haben, hat jede Hyperbel zwei Asymptoten. Denken Sie daran, dass eine Asymptote eine gerade Linie ist, die einer Funktion sehr nahe kommt, sie aber nie ganz schneidet oder berührt.

Die Formeln, die den Asymptoten der Hyperbeln entsprechen, lauten also:

$y= \cfrac{b}{a} x$

$y= -\cfrac{b}{a}x$

Damit lassen sich die Asymptoten jeder Hyperbel anhand ihrer Koeffizienten leicht bestimmen

$a$

Und

$b,$

Dies sind jeweils die Längen der realen Halbachse und der imaginären Halbachse der Hyperbel.

Exzentrizität der Hyperbel

Die Exzentrizität einer Hyperbel ist ein charakteristischer Parameter, der bestimmt, wie offen oder geschlossen sie ist. Numerisch wird die Exzentrizität einer Hyperbel berechnet, indem man ihre halbe Brennweite durch ihre reale Halbachse dividiert:

$e=\cfrac{c}{a}$

Die Exzentrizität jeder Hyperbel ist immer größer als 1:

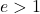
$e>1″ title=“Rendered by QuickLaTeX.com“ height=“14″ width=“40″ style=“vertical-align: -2px;“></p> </p> <p> Der Wert dieses Parameters ist sehr relevant, da er die Form einer bestimmten Hyperbel angibt. Je näher die Exzentrizität einer Hyperbel bei 1 liegt, desto geschlossener sind ihre Äste; Andererseits sind die Zweige umso offener, je größer der Wert der Exzentrizität ist. </p> <figure class=$

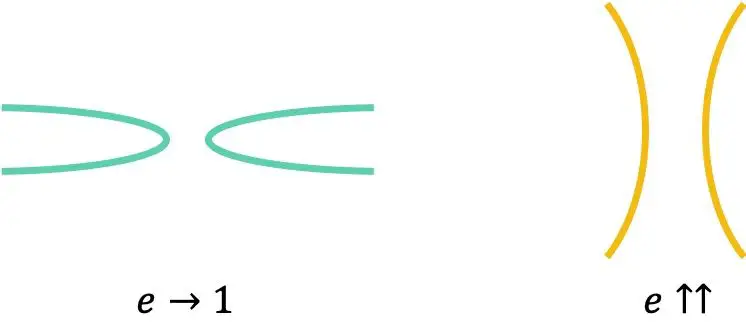
Abschließend ist zu beachten, dass die Exzentrizität einer gleichseitigen Hyperbel immer gleich ist

$\sqrt{2}.$

Hyperbelprobleme gelöst

Nachfolgend können Sie die Konzepte, die wir gesehen haben, anhand von Problemen und gelösten Übungen zu Hyperbeln und der Hyperbelgleichung üben.

Übung 1

Wie lautet die Gleichung der Hyperbel mit Mittelpunkt im Punkt (-1,3), Länge der realen Halbachse von 3 Einheiten und Länge der imaginären Halbachse (parallel zur Y-Achse) von 7 Einheiten?

siehe Lösung

Um die Gleichung der Hyperbel zu finden, wenden Sie einfach die Formel für die gewöhnliche Gleichung der Hyperbel an:

$\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1$

Wir setzen die Koordinaten des Mittelpunkts der Hyperbel in die Gleichung ein:

$\cfrac{(x-(-1))^2}{a^2}-\cfrac{(y-3)^2}{b^2} = 1$

$\cfrac{(x+1)^2}{a^2}-\cfrac{(y-3)^2}{b^2} = 1$

Und schließlich ersetzen wir die Werte der Unbekannten

$a$

Und

$b:$

$\cfrac{(x+1)^2}{3^2}-\cfrac{(y-3)^2}{7^2} = 1$

$\cfrac{\bm{(x+1)^2}}{\bm{9}}\bm{-}\cfrac{\bm{(y-3)^2}}{\bm{49}} \bm{= 1}$

Übung 2

Finden Sie die Koordinaten des Mittelpunkts, der Eckpunkte, der Brennpunkte, den Wert der Exzentrizität und die Asymptoten der Hyperbel, deren Gleichung definiert ist durch:

$\cfrac{x^2}{25}-\cfrac{y^2}{144} = 1$

siehe Lösung

Zunächst ist zu beachten, dass die negative Variable in der Gleichung die Variable y ist, sodass sich die Zweige der Hyperbel nach rechts und links öffnen (Brennachse parallel zur X-Achse).

Zweitens entspricht die Gleichung der kanonischen (oder reduzierten) Gleichung der Hyperbel, sodass ihr Mittelpunkt der Koordinatenursprung ist.

$\bm{O(0,0)}$

Sobald wir den Mittelpunkt der Hyperbel kennen, müssen wir zur Berechnung aller anderen Punkte den Wert der realen Halbachse (Parameter) ermitteln

$a$

) und die imaginäre Halbachse (Parameter

$b$

). Beides können wir aus der Formel der kanonischen (oder reduzierten) Gleichung der Hyperbel ableiten:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1$

$\cfrac{x^2}{25}-\cfrac{y^2}{144} = 1$

$a^2 = 25$

$a = \sqrt{25}$

$a = 5$

$b^2 = 144$

$b= \sqrt{144}$

$b = 12$

Wenn also zwischen dem Mittelpunkt und den Eckpunkten ein Abstand von 5 Einheiten besteht, bedeutet dies, dass die Eckpunkte der Hyperbeln wie folgt sind:

$\bm{A(-5,0) \qquad A'(5,0)}$

Um die Koordinaten jedes Brennpunkts zu bestimmen, müssen Sie den Wert der halben Brennweite (Parameter) kennen

$c$

). Und dazu können wir die Formel verwenden, die die Elemente einer Hyperbel verbindet:

$c^2 = a^2+b^2$

$c = \sqrt{a^2+b^2}$

$c = \sqrt{5^2+12^2} = \sqrt{169} =13$

Zwischen dem Zentrum und den Häusern liegt somit eine Fläche von 13 Einheiten. Somit sind die Koordinaten jedes Haushalts:

$\bm{F(-13,0) \qquad F'(13,0)}$

Um dann die Exzentrizität der Hyperbel zu berechnen, müssen wir die entsprechende Formel verwenden:

$e= \cfrac{c}{a} = \cfrac{13}{5} = \bm{2,6}$

Und schließlich finden wir die Asymptoten der Hyperbel mit ihren Formeln:

$y= \cfrac{b}{a} x \ \longrightarrow \ \bm{y=}\mathbf{\cfrac{12}{5}}\bm{ x}$

$y= -\cfrac{b}{a}x \ \longrightarrow \ \bm{y=-}\mathbf{\cfrac{12}{5}}\bm{ x}$

Übung 3

Berechnen Sie die Gleichung der Hyperbel mit dem Mittelpunkt im Koordinatenursprung unter der Bedingung, dass der Unterschied in den Abständen von einem Punkt der Hyperbel zu den Brennpunkten F(-4,0) und F(4,0) 6 Einheiten beträgt.

siehe Lösung

Da die Hyperbel den Mittelpunkt im Koordinatenursprung hat, verwenden wir zunächst die kanonische oder reduzierte Gleichung:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1$

Dann muss gemäß der Definition einer Hyperbel der Absolutwert der Differenz der Abstände von einem ihrer Punkte zu den Brennpunkten (in diesem Fall 6) gleich der Länge der realen Achse sein (

$2a$

). Noch:

$\lvert d_1 - d_2 \rvert = 2a$

$6 = 2a$

$\cfrac{6}{2} = a$

$3 = a$

Andererseits ist der Mittelpunkt der Hyperbel der Punkt (0,0) und ein Fokus ist der Punkt (4,0). Damit ist der Abstand zu den beiden Punkten (Parameter

$c$

) sind 4 Einheiten.

$c =4$

Wir können nun den Wert des Parameters kennen

$b$

mit dem mathematischen Zusammenhang zwischen den 3 charakteristischen Koeffizienten der Hyperbel:

$c^2 = a^2+b^2$

$b^2 = c^2-a^2$

$b = \sqrt{c^2-a^2}$

$b= \sqrt{4^2-3^2} = \sqrt{16-9} =\sqrt{7}$

Die Gleichung der Hyperbel lautet also:

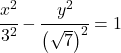
$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1$

$\cfrac{x^2}{3^2}-\cfrac{y^2}{\left(\sqrt{7}\right)^2} = 1$

$\cfrac{\bm{x^2}}{\bm{9}}-\cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$

Übertreibung: definition, formel, elemente, gleichung, beispiele,…

Was ist eine Übertreibung?

Elemente einer Hyperbel

Beziehung zwischen den Elementen einer Hyperbel

Hyperbelgleichung

Gewöhnliche Gleichung der Hyperbel

Kanonische oder reduzierte Gleichung der Hyperbel

Allgemeine Gleichung der Hyperbel

Gleichseitige Hyperbelgleichung

konjugierte Hyperbeln

Asymptoten der Hyperbel

Exzentrizität der Hyperbel

Hyperbelprobleme gelöst

Übung 1

Übung 2

Übung 3

Kommentar verfassen Kommentieren abbrechen